
Пирогов. Сопротивление материалов 2008
.pdf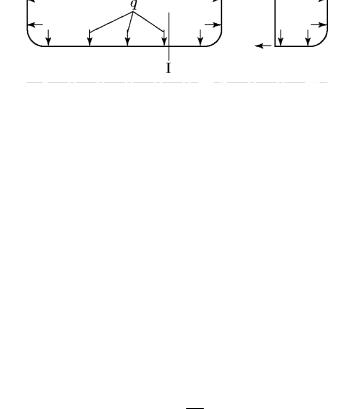
По условиям полной симметрии
σm = σt .
Согласно уравнению (10.1):
σm = σt = qR2δ .
Напряженное состояние двухосное:
σ = σ |
2 |
= qR |
, |
σ |
3 |
= 0 . |
1 |
2δ |
|
|
|
||
|
|
|
|
|
|
Пример 8. Цилиндрический сосуд с днищами (рис. 62, а) находится под действием внутреннего давления q. Радиус цилиндра равен R, толщина стенки – δ. Определить напряжения в стенке цилиндра.
а |
б |
Рис. 62
Отсекаем поперечным сечением I – I часть цилиндра (рис. 62, б) и составляем для нее уравнение равновесия. Согласно первой теореме равнодействующая (Q) сил внутреннего давления на днище
будет равна
Q = π R2 q.
Эта сила уравновешивается меридианальными напряжениями, действующими в поперечном сечении цилиндрической оболочки
σт2πRδ= πR2 q.
Таким образом,
σm = 2Rδq .
111

Для цилиндра ρm = ∞, ρt = R . Из формулы (10.1) находим
σt = Rδ q .
Полученный результат свидетельствует о том, что максимальное напряжение в цилиндрической оболочке вдвое больше напряжения в сферической оболочке того же радиуса и той же толщины. Понятно, что сферическая форма оболочки более рациональна для содержания газа с высоким давлением.
Пример 9. Конический сосуд, геометрические размеры которого представлены на рис. 63, а, заполнен жидкостью с удельным весом γ. Допустимое напряжение – [σ]. Рассчитать напряжения в сосуде, построить эпюры σт и σt и определить толщину сосуда, используя третью теорию прочности.
Нормальным коническим сечением (вершина конуса в точке А) отсекаем нижнюю часть конической оболочки высотой х (рис. 63, г) и составляем для нее уравнение равновесия:
2πrx δσm cosα =Q ,
где Q – равнодействующая давления жидкости на отсеченную часть оболочки. Согласно теореме 2, Q равна весу жидкости в объеме, расположенном над поверхностью отсеченной части конуса. Этот объем равен сумме объема отсеченного конуса высотой х и объема цилиндра радиусом rx и высотой (h – х). Таким образом,
получаем
|
2 1 |
2 |
|
|
Q = γ |
πrx |
3 |
x +πrx |
(h − x) . |
|
|
|
|
|
Учитывая, что rx = x tg α , получаем выражение для σm :
|
γ tg α |
|
|
2 |
|
2 |
|
σm = |
|
|
− |
|
x |
|
+ xh . |
|
3 |
|
|||||
|
2δcosα |
|
|
|
|
||
Максимального значения σm достигает для сечения с координа-
той x = 0,75h :
σm|x=0,75h = 16δ cosα γh2.
112
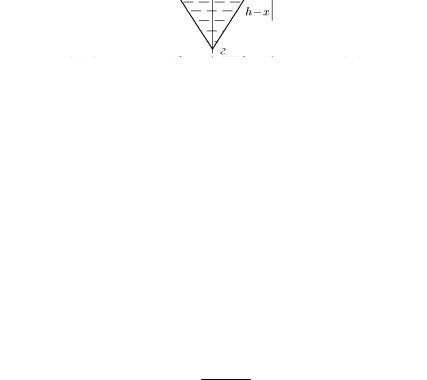
Рис. 63
Для сечения с координатой х = h:
σm |x=h = 6δtgcosαα γh2.
Эпюра σm представлена на рис. 63, б. Запишем уравнение Лапласа:
|
|
|
|
σm |
+ |
σt |
|
= |
q(x) |
. |
|
|
||||
|
|
|
|
|
|
ρ |
|
|
|
|||||||
|
|
|
|
ρ |
m |
|
|
|
δ |
|
|
|||||
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|||
В нашем случае |
ρm =∞, |
|
а q(х) − гидростатическое давление |
|||||||||||||
жидкости, т. е. q(x) = γ(h − x) . |
|
|
|
|
|
|||||||||||
Радиус кривизны ρt |
равен: |
|
|
|
|
|
||||||||||
ρt |
= |
|
rx |
|
|
= |
x tgα |
= xsinα |
1 |
. |
||||||
cosα |
cosα |
cos2 α |
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
113 |
|

Получаем выражение для σt в виде
σt = |
γ(h − x)x |
sin α |
1 |
. |
|
cos2 α |
|||
|
δ |
|
||
Максимального значения окружное напряжение достигает для x = h2 (посередине высоты конуса):
|
h |
|
γh2 |
|
1 |
|
|
σt x = |
|
|
= |
|
sin α |
|
. |
|
4δ |
cos2 α |
|||||
|
2 |
|
|
|
|||
Эпюра σt представлена на рис. 63, в.
Из анализа эпюр σm и σt очевидно, что наиболее опасными будут точки сечения, где σt принимает максимальное значение, т.е.
посередине высоты конического сосуда. |
В этих точках σ1 = σt , |
|||||||||||||||
σ2 = σm , |
σ3 = 0 . Условие прочности при использовании третьей |
|||||||||||||||
теории прочности запишется следующим образом: |
||||||||||||||||
σ |
экв |
= σ −σ |
3 |
= σ |
t |
−0 = σ |
t |
≤[σ] или |
σt = |
γh2 |
|
sin α |
≤ [σ]. |
|||
|
|
|||||||||||||||
|
1 |
|
|
|
|
|
|
|
4δ cos2 α |
|||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
γh2 sin α |
|
|
|
|
|
|||
|
|
|
|
|
|
δ = |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
4[σ] |
cos2 α |
|
|
|
|
|
|||
114
11. ТОЛСТОСТЕННЫЕ ТРУБЫ
11.1.Дифференциальные уравнения равновесия и совместности деформаций
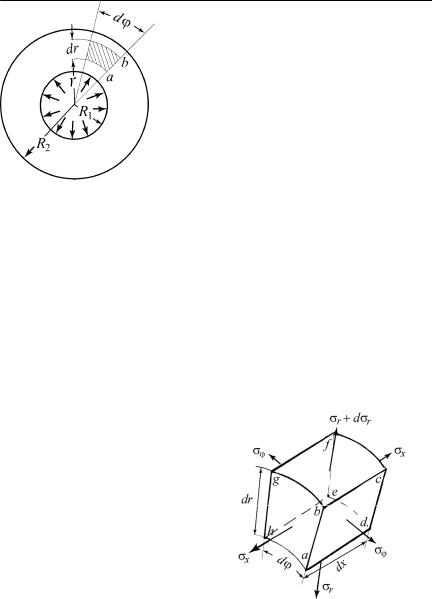
Рассмотрим толстостенную трубу, находящуюся под действием внутреннего давления P (рис. 64).
Решаем задачу в цилиндрической системе координат x, r, φ. Деформированное состояние трубы будет осесимметричным,
т.е. каждая точка будет перемещаться только в направлении радиуса и параллельно оси трубы x, причем эти перемещения не зависят от полярного угла φ.
Для трубы со свободными торцами все сечения трубы, перпендикулярные к ее оси, остаются плоскими, иначе говоря, радиальные перемещения зависят только от радиуса, а осевые – только от x. В других случаях это утверждение верно для сечений, достаточно удаленных от торцов (принцип Сен-Венана).
Вырежем из цилиндра двумя перпендикулярными к его оси плоскостями, расстояние между которыми dx, кольцо (см. рис. 64). Двумя осевыми плоскостями и двумя концентрическими цилиндрическими поверхностями выделим из кольца элемент в форме криволинейного шестигранника (рис. 65). Размеры этого шестигранника:
dr, dx, rdφ и (r + dr) dφ.
Рис. 64 |
Рис. 65 |
115
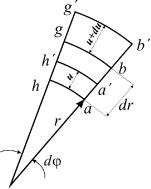
В осевых сечениях цилиндра (плоскости abcd и efgh) по условиям симметрии касательные напряжения отсутствуют и действуют только нормальные напряжения σϕ , называемые окружными. В
поперечных сечениях цилиндра (плоскости abgh и cdef) могут существовать нормальные напряжения σx (например, при наличии у
трубы днищ). Эти напряжения предполагаются неизменяемыми как по оси, так и по радиусу цилиндра. Касательные напряжения в поперечных сечениях отсутствуют, так как плоскости этих сечений не искривляются и точки сечений перемещаются только в радиальном и осевом направлениях. Поскольку площадки abcd и cdef свободны от касательных напряжений, от этих напряжений будут свободны цилиндрические поверхности adeh и bcfg. Напряжение на поверхности adeh обозначим через σr и назовем его радиальным. При пе-
реходе от радиуса r к r + dr (от поверхности adeh к поверхности bcfg) напряжение σr получит приращение dσr .
Проецируя усилия, действующие на элемент, на направление
биссектрисы угла dφ и принимая sin |
d ϕ |
≈ |
d ϕ |
(dφ мал), получим |
|
|
|||
2 |
2 |
|
||
следующее дифференциальное уравнение равновесия:
(σr + dσr )(r + dr)d ϕdx −σrrd ϕdx −σϕdr dx d ϕ = 0
или, пренебрегая малыми величинами высшего порядка, получаем выражение:
σ |
r |
−σ |
ϕ |
+ |
dσr |
r = 0 . |
(11.1) |
|
|||||||
|
|
|
dr |
|
|||
Остальные |
уравнения равновесия |
||||||
элемента |
удовлетворяются |
тождест- |
|||||
венно. |
|
|
|
|
|
|
|
Рассмотрим |
|
деформации |
того же |
||||
элемента. Обозначим через u радиальное перемещение точки, находящейся на расстоянии r от оси (точки a и h на рис. 66).
Дуга ah займет положение a′h′ по- |
|
|
сле нагружения трубы. Относительное |
Рис. 66 |
|
удлинение дуги ah равно: |
||
|
||
116 |
|

εϕ = |
(r +u)dϕ−rdϕ |
= u . |
(11.2) |
|
rdϕ |
||||
|
r |
|
Точка b после деформации займет положение b′ , ее перемещение есть u + du. Новая длина элемента ab (a′b′) будет равна dr + du, а его относительное удлинение:
|
|
εr = du . |
|
(11.3) |
|
|
|
|
dr |
|
|
Дифференцируя выражение (11.2), получим |
|
||||
|
dεϕ |
+ |
εϕ −εr |
= 0 . |
(11.4) |
|
dr |
r |
|||
|
|
|
|
||
Соотношение (11.4) называется уравнением совместности деформаций.
11.2.Определение напряжений и перемещений в толстостенной трубе
Напряжения в толстостенной трубе могут быть выражены через деформации по формулам закона Гука (4.4), в которых индексы y, z заменены индексами r и φ:
εx = E1 [σx −μ(σr +σϕ)],
εr = E1 [σr −μ(σϕ +σx ],
εϕ = E1 [σϕ −μ(σx + σr ].
Из первого уравнения системы (11.5) следует:
σx = Eεx +μ(σr + σϕ) .
Из последних двух уравнений (11.5) получаем:
σr = 1−Eμ2 (εr +μεϕ) +1−μμσx , σϕ = 1−Eμ2 (εϕ +μεr ) +1−μμσx .
(11.5)
(11.6)
(11.7)
117
Подставляя сюда εϕ и εr |
из выражений (11.2) и (11.3), полу- |
|||||||||||||||||
чим: |
|
|
|
E |
|
du |
|
|
u |
|
|
|
μ |
|
||||
σr = |
|
|
|
|
+μ |
+ |
|
|
σx , |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
−μ2 |
|
|
1 |
−μ |
|||||||||||||
|
|
dr |
|
|
r |
|
(11.8) |
|||||||||||
σϕ = |
|
|
|
E |
|
u |
+μ |
du |
|
|
|
μ |
||||||
|
|
|
|
+ |
|
|
σx . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
−μ2 |
|
|
|
1 |
−μ |
||||||||||||
|
|
r |
|
|
dr |
|
|
|||||||||||
Используя соотношения (11.8), |
запишем уравнение равновесия |
|||||||||||||||||
(11.1) в перемещениях: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2u |
|
+ |
1 du |
− |
u |
= 0 . |
(11.9) |
||||||||
|
|
|
|
dr2 |
r dr |
r2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Уравнение (11.9) – линейное однородное дифференциальное
уравнение второго порядка типа Эйлера. Как известно, его частные
решения имеют вид |
|
u = r n . |
(11.10) |
Подставляя выражение (11.10) в уравнение (11.9), получаем после сокращения на rn−2 характеристическое уравнение:
n2 −1 = 0 .
Корням этого уравнения n1 =1, n2 = −1 соответствуют частные
решения r и 1 . Общее решение найдем, |
умножив эти частные ре- |
||||||||||||||||||||||||||||
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
шения на постоянные интегрирования C1 и C2 |
и затем сложив их: |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
u =C r + |
C2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.11) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Подставляя выражение (11.11) в формулы (11.8), находим: |
|||||||||||||||||||||||||||||
σ |
r |
= |
|
E |
|
C (1+μ)−C |
2 |
|
1−μ |
|
+ |
|
|
|
μ |
|
σ |
x |
, |
||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
1−μ |
2 |
|
1 |
|
|
|
r |
2 |
|
|
|
1 |
−μ |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.12) |
|||||||||||
|
|
|
|
E |
C (1+μ)+C |
|
|
|
1−μ |
|
|
|
|
|
μ |
|
|
|
|||||||||||
σ |
ϕ |
= |
|
2 |
|
|
+ |
|
|
|
σ |
x |
. |
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
1−μ |
2 |
|
1 |
|
|
|
|
r |
2 |
|
|
|
|
1 |
−μ |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Постоянные C1 |
и C2 определяем из следующих граничных усло- |
||||||||||||||||||||||||||||
вий: при r = R1 |
|
σr = −P ; при r = R2 |
|
σr =0 , откуда |
|
|
|
||||||||||||||||||||||
118 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1−μ)PR2 |
|
σ |
x |
|
|
C |
= |
|
1 |
−μ |
|
, |
|
E(R2 |
− R2 ) |
|
|
||||
1 |
|
|
E |
||||
|
|
2 |
1 |
|
|
|
|
(1 + μ)PR2R2
C2 = 2 − 1 2 2 .
E(R2 R1 )
Подставляя C1 и C2 в формулы (11.12), получаем окончательные выражения для радиальных и окружных напряжений:
|
|
|
R2 P |
|
|
|
|
R2 |
|
|
|
|
σ |
|
= |
|
1 |
|
1 |
− |
2 |
|
|
, |
|
|
R2 |
− R2 |
|
r2 |
||||||||
|
r |
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
1 |
|
|
|
|
|
|
|
(11.13) |
|
|
|
R P |
|
|
|
|
R2 |
|
|
||
|
|
|
|
|
|
|
|
|||||
σ |
|
= |
|
1 |
|
1 |
+ |
|
2 |
|
. |
|
|
R2 |
− R2 |
|
r2 |
|
|||||||
|
ϕ |
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
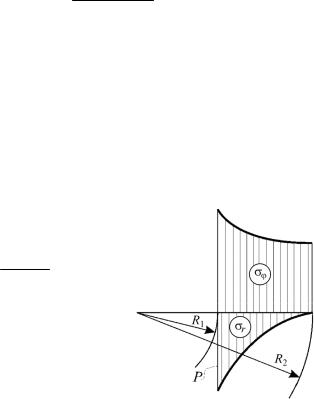
На рис. 67 представлены эпюры радиальных и окружных напряжений.
Согласно формуле (11.6) осевое напряжение будет постоянно по толщине стенки и равно:
PR2
σx = Eεx +2μ 1 . (11.14)
R22 − R12
Следовательно, полученное решение строго верно в тех случаях, когда к торцам трубы приложены равномерно распределенные растягивающие или сжимающие внешние силы (в частном случае эти си-
лы могут быть равны нулю). Равно- Рис. 67 действующую внутренних сил в поперечном сечении обозначим че-
рез N. Площадь поперечного сечения трубы равна π(R22 −R12 ) . Если труба имеет днища, растягивающая сила N равна равнодействующей давления на дно, площадь которого есть πR12 . В этом случае осевые напряжения будут равны:
|
N |
|
PR2 |
|
|
||
σx = |
или σx = |
|
1 |
, |
(11.15) |
||
π(R2 |
− R2 ) |
R2 |
− R2 |
||||
|
2 |
1 |
2 |
1 |
|
119 |
|
|
|
|
|
|
|
|
|
а относительное осевое удлинение трубы согласно (11.5):
εx = |
PR1 |
(1−2μ) |
1 |
. |
(11.16) |
|
R2 |
− R2 |
E |
||||
|
2 |
1 |
|
|
|
|
В открытой по концам трубе (например, ствол орудия во время выстрела) σx = 0 , поэтому:
εx = −2μ |
PR1 |
|
||
|
|
. |
(11.17) |
|
R2 |
− R2 |
|||
2 |
1 |
|
|
|
Рассмотрим теперь радиальное перемещение в цилиндре. Подставляя значения C1 и C2 в уравнение (11.11), находим:
|
(1−μ)R2 P |
|
(1+μ)PR2R2 |
|
μσ |
x r . |
||
u = |
|
1 |
r + |
|
1 2 |
− |
|
|
E(R2 |
− R2 ) |
E(R2 |
− R2 )r |
E |
||||
|
2 |
1 |
|
2 |
1 |
|
|
|
Если осевая сила отсутствует, то σx = 0 и в этом случае:
|
(1 |
−μ)R2P |
|
(1+μ)PR2R2 |
|||
u = |
|
|
1 |
r + |
|
1 2 |
. |
E(R2 |
− R2 ) |
E(R2 |
|
||||
|
|
− R2 )r |
|||||
|
|
2 |
1 |
|
2 |
1 |
|
(11.18)
(11.19)
Если цилиндр имеет днища, σx определяется согласно выражению (11.15) и в этом случае:
|
(1−2μ)R2P |
|
(1+μ)R2 R2 P |
|
|
||||
u = |
|
1 |
|
r + |
|
1 2 |
. |
(11.20) |
|
E(R2 |
− R |
2 ) |
Er(R2 |
− R2 ) |
|||||
|
|
|
|
||||||
|
2 |
1 |
|
2 |
1 |
|
|
||
120
