Пирогов. Сопротивление материалов 2008

4.СВЯЗЬ МЕЖДУ НАПРЯЖЕНИЯМИ И ДЕФОРМАЦИЯМИ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ. ЭНЕРГИЯ УПРУГОЙ ДЕФОРМАЦИИ

4.1. Закон Гука для чистого сдвига

Опытным путем установлена линейная зависимость относительного сдвига (угла сдвига) от касательного напряжения:

где G – модуль сдвига (модуль упругости второго рода). Он характеризует способность материала сопротивляться деформации сдвига. Для материала, находящегося в упругом состоянии, установлена связь между Е, G и μ:

4.2.Закон Гука для трехосного напряженного состояния, заданного главными напряжениями

Используя принцип независимости действия сил, объемное напряженное состояние можно представить как сумму трех одноосных напряженных состояний А, В и С (рис. 22).

Рис. 21

Запишем деформации для всех трех случаев:

для А: ε1A = σE1 , ε2A = ε3A = −μ σE1 ;

41

для B: ε1B = ε3B = −μ σE2 , ε2B = σE2 ;

для С: ε1C = εC2 = −μ σE3 , εC3 = σE3 .

Тогда при одновременном действии трех главных напряжений

4.3.Обобщенный закон Гука

Вслучае, когда напряженное состояние задано шестью компонентами напряжений, его можно представить как сумму напряженных состояний А и В (рис. 23). В состоянии А элементарный куб испытывает только линейные деформации, так как грани куба сво-

бодны от касательных напряжений. Напряжения σx , σy , σz в со-

стоянии А являются главными и тогда, учитывая (4.3), можно записать деформации в направлении осей х, у и z:

εz = E1 [σz −μ(σx + σy )].

Всостоянии В элементарный куб испытывает только деформа-

ции сдвига, так как касательные напряжения не могут вызвать удлинения ребер куба в направлении осей x, у и z. В соответствии с законом Гука для чистого сдвига (4.1) имеем

42

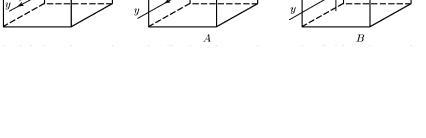
Рис. 23

Совокупность шести уравнений (4.4) и (4.5) выражает обобщенный закон Гука для трехосного напряженного состояния в общем случае.

4.4. Объемная деформация

Пусть ребра элементарного куба до деформации имели длину, равную единице. После приложения внешней нагрузки вдоль ребер стали действовать главные напряжения, которые вызвали относительные удлинения ребер, равные ε1 , ε2 и ε3 . Учитывая началь-

ную длину ребер, можно записать, что удлинения ребер соответственно равны ε1 , ε2 и ε3 . Новый объем куба VK будет равен:

VK = (1 + ε1)(1 + ε2 )(1 + ε3 ) .

Из-за малости ε1 , ε2 и ε3 по сравнению с единицей пренебрега-

ем их произведениями и получаем

VK ≈1+ε1 +ε2 +ε3 .

Начальный объем куба V0 =1 . Тогда относительное изменение объема εV будет равно:

Подставим формулы (4.3) в выражение (4.6) и получим:

43

Учитывая инвариантность суммы нормальных напряжений для

4.5. Удельная потенциальная энергия упругой деформации

При статическом нагружении считается, что работа внешних сил полностью (без потерь) переходит в потенциальную энергию упругой деформации. Удельная потенциальная энергия определяется путем деления потенциальной энергии, накопленной нагруженным телом, на его объем.

меняется пропорционально смещению (закон Гука для чистого сдвига) и совершает работу

0,5τyx dx dz γyx dy .

Выражения для остальных слагаемых потенциальной энергии упругой деформации получаются простой перестановкой индексов.

44

В итоге потенциальная энергия (dU), накопленная элементарным объемом, будет равна:

dU = 0,5 dx dy dz (σxεx +σyεy +σzεz +τxyγxy + τyz γyz +τzxγxz ) .

Разделим обе части равенства на элементарный объем и выразим деформации через напряжения по формулам (4.4)–(4.5).

Получим выражение для удельной потенциальной энергии а в виде:

Очевидно, что потенциальная энергия во всем объеме тела будет равна:

U = ∫adV .

V

Представим теперь напряженное состояние, заданное главными напряжениями, как сумму двух напряженных состояний

(рис. 25), где σcp = 13 (σ1 + σ2 + σ3 ) , σ1′ = σ1 −σcp , σ′2 = σ2 −σcp и σ′3 = σ3 −σcp .

Для трехосного растяжения элементарного куба под действием напряжений σcp характерно сохранение формы. Изменение объема

согласно (4.7) εV = 1 −E2μ 3σcp , или

εV = 1−E2μ (σ1 +σ2 +σ3 ) .

Накопленная удельная потенциальная энергия, связанная с изменением объема (aоб) согласно (4.10), будет равна:

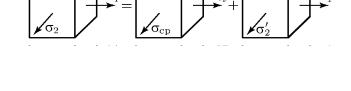
Рис. 25

Для второго напряженного состояния (второе слагаемое) объем не меняется. Вся деформация, а следовательно, и накопленная потенциальная энергия связаны с изменением формы (aф) . Эта энер-

гия находится путем вычитания aоб из а, т. е. выражения (4.11) из

Эта энергия называется удельный потенциальной энергией изменения формы (или формоизменения).

46

5. ТЕОРИИ ПРОЧНОСТИ

Для расчета на прочность в условиях сложного напряженного состояния, строго говоря, необходимо было бы иметь диаграммы испытаний для любой комбинации главных напряжений, характеризующих напряженное состояние в точке. Однако понятно, что практически невозможно реализовать экспериментально бесчисленное множество напряженных состояний. Поэтому необходимо найти такой прием, который позволил бы по экспериментальным данным, полученным при растяжении или сжатии, проводить оценку прочности в условиях любого напряженного состояния.

Предварительно введем понятие об эквивалентном напряжении.

Эквивалентное напряжение σэкв – такое напряжение, которое

следует создать в растянутом или сжатом образце, чтобы его напряженное состояние было равноопасно с заданным.

Понятно, что в расчетах на прочность σэкв должно быть меньше

допускаемого напряжения, которое определяется экспериментально при растяжении или сжатии. Задача заключается в том, как выразить σэкв через σ1 , σ2 и σ3 . Для этого рассмотрим несколько

гипотез, которые легли в основу технических теорий прочности.

5.1.Теория максимального нормального напряжения (первая теория прочности)

Воснове этой теории лежит предположение о том, что два напряженных состояния будут равноопасны (эквивалентны), если у них равны максимальные нормальные напряжения, т.е.

В практических расчетах первая теория прочности в настоящее время почти не применяется. Она дает совпадение расчета с экспериментом при растяжении хрупких материалов, когда σ1 по абсо-

лютной величине значительно больше других напряжений.

47

5.2.Теория максимальной линейной деформации (вторая теория прочности)

Согласно этой теории два напряженных состояния равноопасны, если у них равны максимальные относительные удлинения.

Для одноосного напряженного состояния максимальное относительное удлинение

ε1ОН = σЕэкв .

Для трехосного напряженного состояния максимальное относительное удлинение:

Эта теория находится в противоречии с экспериментальными данными для пластичных материалов. В настоящее время практически не применяется.

5.3.Теория максимальных касательных напряжений (третья теория прочности)

Воснове третьей теории лежат известные данные о том, что пластическая деформация реализуется за счет сдвига под действием касательных напряжений. Поэтому естественно принять в качестве критерия перехода из упругого состояния в пластическое наибольшее касательное напряжение в точке.

Согласно (3.9) τmax =0,5(σ1 −σ3 ) .

Для одноосного напряженного состояния максимальное касательное напряжение τОНmax равно:

τОНmax =0,5σэкв .

48

Следовательно,

так как два напряженных состояния будут равноопасны, если у них максимальные касательные напряжения будут равны. Условие прочности по этой теории имеет вид:

Эта теория применяется для пластичных материалов. Для хрупких материалов она не применима.

5.4.Энергетическая теория прочности (четвертая теория прочности)

Всоответствии с четвертой теорией два напряженных состояния равноопасны, если их удельные потенциальные энергии изменения формы равны.

Для одноосного напряженного состояния эта энергия aФОН согласно (4.12) равна:

Условие прочности по четвертой теории имеет вид:

Эта теория широко используется при расчете конструкций из пластичных материалов, одинаково сопротивляющихся растяжению и сжатию. Для хрупких материалов она не пригодна.

49

5.5. Теория Мора

Теория прочности Мора не содержит критериальных гипотез и основана в первую очередь на логической систематике экспериментальных результатов. Ее основное допущение заключается в том, что главное напряжение σ2 не оказывает влияния на проч-

ность. Для получения выражения для σэкв строятся круги Мора

для предельных напряженных состояний, т.е. состояний, при которых начинается пластическое деформирование или разрушение. Круги для одноосного сжатия и одноосного растяжения строятся достаточно достоверно, так как одноосное растяжение и одноосное сжатие легко реализуются экспериментально. К этим кругам проводится общая касательная, которая в некотором приближении рассматривается как огибающая предельных кругов Мора (диаграмм для предельных напряженных состояний). Предельные круги Мора для любого напряженного состояния не должны выходить за огибающую. Опуская дальнейшие геометрические построения, дадим окончательный результат для эквивалентного напряжения:

где k = σтр – для пластичных материалов.

σтс

Наилучшие результаты эта теория дает для случая, когда σ1 >0 , а σ3 <0 . Это обстоятельство существенно, так как при решении

практических задач напряженное состояние такого рода встречается чаще других. Для многих пластичных материалов, у которых σтр = σтс , теория прочности Мора совпадает с теорией максималь-

ных касательных напряжений.

50