Билет 12. Графические характеристики случайных величин. Гистограмма. Характеристики положения (мода, медиана, выборочная средняя). Примеры.

Полигон частот – ломаная линия, отрезки которой соединяют точки с координатами (x₁; n₁), (x₂;n₂).

Гистограмма частот – совокупность смежных прямоугольников, построенных на одной прямой линии, основания прямоугольников одинаковы и равны a, а высоту равны отношению частоты к a.

Наиболее распространёнными характеристиками статистического распределения являются средние величины: мода, медиана и выборочная средняя.

Медиа́на— равна варианте, которая расположена в середине статистического распределения, делит статистический ряд на два равные части.

Мода – равна варианте, которой соответствует наибольшая частота.

Выборочная средняя – определяется как среднее арифметическое значение вариант статистического ряда.

Билет 13. Прямые и косвенные измерения. Погрешности измерений. Абсолютная и относительная погрешности измерений. Систематическая, приборная, грубая, случайная погрешности. Примеры.

При прямом измерении числовые значения искомой величины получаются непосредственным сравнением её с мерой (пример – измерение температуры тела медицинским термометром)

Косвенные измерения – это измерения, которые сводятся к нахождению искомой величины по известной зависимости между нею и непосредственно измеренными величинами (например, определение массы тела при взвешивании с учетом выталкивающей силы, определение вязкости жидкости по скорости падения в ней шарика)

Погрешность измерений - это количественная характеристика качества измерений.

x_i = x_i – X₀

Абсолютная погрешность измерения( x) – это разность между результатом измерения и истинным значением измеряемой величины.

Качество измерений характеризуется относительной погрешностью, которая показывает процентную долю погрешности от истинного значения измеряемой величины

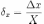* 100%

В величины погрешностей измерений дают вклад несколько различных источников. Им соответствуют, так называемые, грубые, систематические, инструментальные (приборные) и случайные погрешности.

Грубые погрешности – резко изменяют результат измерения и возникают в результате промахов, допускаемых персоналом и неконтролируемых резких изменений в условиях измерений.

Систематические погрешности – имеют постоянные по величине и знаку значения, в ходе всей серии повторных измерений и возникают в результате дефектов измерительных приборов или нарушения методики измерений.

Приборные погрешности – являются характеристикой любого измерительного инструмента и не могу быть равны нулю

Случайные погрешности – являются следствием непредсказуемых статических процессов и объекте измерения, и измерительном приборе, а также случайных измерений в условиях проведения опыта. (например, показания электронного термометра, измеряющего температуру воздуха будут варьировать в результате конвекции, вариаций напряжения питания датчика температуры.)

Билет 14. Методы оценки приборной и случайной погрешностей. Коэффициент Стьюдента. Методы оценки косвенных измерений. Примеры.

Для оценки приборных и случайных погрешностей нужно предварительно исключить грубые и систематические погрешности. Случайные погрешности подчиняются нормальному распределению. Искомый результат оказывается в доверительном интервале

X ₀ = x + S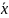 - когда a = 68% (a – доверительный интервал)

X ₀ = x + 2S – когда a = 95%

X ₀ = x + 3S – когда а = 99,7%

При малом объёме выборки (5,4,3 измерения) доверительные интервалы для результатов измерений определяют по формуле:

X ₀ = x + t_aⁿ S_x , где t_aⁿ – коэффициент Стьюдента для различных a – доверительных вероятностей, n – числа повторных измерений. S_x - среднее квадратическое среднего арифметического выборки.

Если учесть вклад инструментальной (приборной) погрешности, то общая погрешность будет равна квадратному корню из суммы квадратов случайной и приборной погрешностей.

(брать из методички Монича и Малиновской, с. 115 внизу)

Методы оценки косвенных измерений:

Погрешность косвенных измерений определяется как корень из суммы квадратов частных производных по прямо измеряемым величинам, помноженных на погрешности измеряемых величин.

(брать с. 117 методичка Монича и Малиновской)

Пример – в ходе одной из лабораторных работ были определены погрешности косвенных измерений импеданса живой ткани на разных частотах.