Билет 9. Стандартное нормальное распределение. Стандартные интервалы. Понятия доверительного интервала и доверительной вероятности.

Нормальное распределение с М = 0 и σ = 1 называется стандартным. Если случайная величина Х имеет нормальное распределение с параметрами μ и σ, то случайная величина Х₀ = (Х - μ)/σ имеет стандартное нормальное распределение.

Для непрерывных случайных величин описывается законом Гаусса распределение вероятностей, которое задается функцией плотности распределения:

Одной из важнейших задач, решаемых в рамках теории вероятностей и математической статистики, является определение интервала, в который случайная величина попадёт с некоторой заданной вероятностью. Такая вероятность называется доверительной, а интервал называется доверительным интервалом. Обычно в этих задачах рассматриваются только определённые, стандартные доверительные интервалы. Это позволяет избежать математических вычислений, взяв известные из таблиц доверительные вероятности для стандартных интервалов. Известны три стандартных интервала, основанные на величине среднего квадратического для данного нормального распределения.

1. М- σ <х< М+ σ (α = 68%)

2. М- 2σ <х< М+ 2σ (α = 95%)

3. М- 3σ <х< М+ 3σ (α = 99,7%)

Билет 10. Понятие генеральной совокупности и выборки. Объём выборки, репрезентативность. Статистическое распределение (вариационный ряд). Примеры. Характеристики выборки

Генеральная совокупность – большая статистическая совокупность, т.е. все возможные показатели.

Выборка – отобранная часть членов генеральной совокупности, выбираемая для совместного изучения.

Объём выборки – это число элементов, выделяемых из генеральной совокупности.

Чтобы выборка наиболее полно отражала состояние генеральной совокупности, она должна обладать репрезентативностью. Репрезентативность обеспечивается методом рандомизации.

Пример: по небольшому числу обследуемого населения можно сделать заключение о заболеваемости определёнными болезнями в данном городе.

Вариационный ряд – это статистическое распределение, состоящее из вариант и соответствующих им частот.

Характеристики выборки:

Среднее арифметическое:

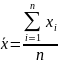
Среднее квадратичное среднего арифметического выборки

где n – объём выборки. Величина среднего арифметического называется также точечной оценкой математического ожидания, а доверительный интервал – интервальной оценкой истинного значения измеряемой величины

Билет 11. Оценка параметров генеральной совокупности по характеристикам её выборки (точечная и интервальная). (Параметры генеральной совокупности и характеристики выборки. Формулы, пояснения).

Генеральная совокупность – большая статистическая совокупность.

Точечная оценка.

И з генеральной совокупности производятся разные выборки одинакового объёма, равным n. Их выборочные средние x₁, x₂, x₃, ..., x_i, ... являются случайными величинами, распределёнными по нормальному закону, их математическое ожидание равно математическому ожиданию генеральной совокупности, т.е. генеральной средней:

При достаточно большой выборке за генеральную среднюю приближённо принимают выборочную среднюю, математическое ожидание дисперсий и среднее квадратическое отклонение различных выборок, составленных из генеральной совокупности, при больших объёмах выборок приближённо равно генеральной дисперсии и генеральному среднему квадратическому отклонению соответственно.

Интервальная оценка

Интервальной оценкой генеральной средней пользуются при небольшом объёме выборки.

В этом случае указывается интервал (доверительный интервал), в котором с определённой (доверительной) вероятностью p находится генеральная средняя. Доверительная вероятность определяет вероятность, с которой генеральная средняя попадает в интервал:

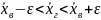
Где положительное число e (эпсилон) характеризует точность оценки.

Наиболее часто p принимает интервалы 0,95; 0,99; 0,999. Чем больше p, тем шире интервал, тем больше e.

Для выборок небольшого объёма в выражении доверительного интервала точность оценки определяется по формуле:

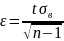
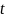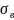– коэффициент Стьюдента, – среднее квадратическое выборки

Соответственно, подставив данное выражение в неравенство

получаем общий вид интервала для генеральной средней в доверительной вероятности