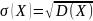Материал к зачёту по математике

Студентки 1 курса 117 группы

педиатрического факультета

Аристовой Ольги Николаевны

Билет 1. Случайное событие. Определение вероятности (статистическое и классическое). Понятие о совместных и несовместных событиях, зависимых и независимых событиях.

Случайное событие – событие, которое в данных условиях может произойти, а может не произойти

Статистическое определение вероятности – это предел, к которому стремится относительная частота появления данного события при неограниченном возрастании числа испытаний.

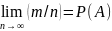
Классическое определение вероятности – это отношение числа ожидаемых событий к полному числу возможных в данном опыте событий.

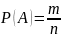
Совместимые события – это события, появление одного из которых не исключает появление другого.

Несовместимые события - это события, появление одного из которых исключает появление другого.

Зависимое событие – это событие, на вероятность которого оказывает влияние исход другого события.

Независимое событие – это событие, на вероятность которого не влияет исход другого события.

Билет 2. Теоремы сложения вероятностей для несовместных и совместных событий.

Теорема сложения вероятностей для несовместных событий:

Вероятность появления какого-либо события из нескольких несовместных равна сумме их вероятностей.

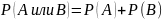
Теорема сложения вероятностей для совместных событий:

Вероятность появления хотя бы одного из нескольких совместных событий равна сомме их вероятностей без вероятности их совместного появления.

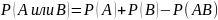
Билет 3. Теоремы умножения вероятностей для независимых и зависимых событий. Условные вероятности.

Теорема умножения вероятностей для независимых событий:

Вероятность совместного появления независимых событий равна произведению их вероятностей.

Теорема умножения вероятностей для зависимых событий:

Вероятность появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже наступили.

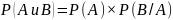
Условная вероятность – вероятность некоторого события при условии того, что другое событие произошло, либо не произошло.

Например, событие А произойдет при условии реализации события В. В таком случае используют обозначение Р(А/В).

Билет 4. Полная вероятность. Теорема Байеса.

Полная вероятность – это вероятность появления некоторого события В, если известны условные вероятности этого события при наличии некоторых событий А_i (которые попарно несовместны, а их объединение есть достоверное событие):

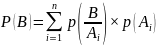
где n – полное число попарно несовместных событий A_i,

p(A_i) – вероятности каждого из этих событий.

Теорема Байеса определяет условную вероятность p(A_k/B) появления некоторого события A_k при условии того, что некоторое событие B уже наступило; здесь k может принимать любое значение от 1 до n, причём n является числом возможных событий, наступающих в данном опыте. Математическое выражение:

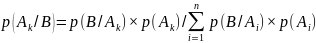
Билет 5. Распределение дискретных случайных величин, их характеристики: математическое ожидание, дисперсия, среднее квадратичное отклонение (формулы, пояснения).

Случайная величина – это величина, значение которой может быть различным в зависимости от случайных обстоятельств.

Если случайная величина принимает конечное счетное значение х1, х2,..., которым сопоставляется n значений вероятностей: Р(х1), Р(х2) и т.д., то распределение называется дискретным, а случайную величину – дискретной.

Характеристики случайных величин

Математическое ожидание дискретной случайной величины – это сумма произведений всех возможных её значений на вероятности этих значений.

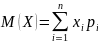
где n – полное число случайных величин.

Дисперсия дискретной случайной величины – это математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

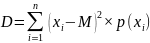
M – математическое ожидание, x_i – случайная величина, р(х_i) – вероятность появления случайной величины

Средним квадратическим отклонением дискретной случайной величины называется квадратный корень из ее дисперсии: