МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ

(НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ)

«МАИ»

Кафедра 403

Расчётно-графическая работа

по дисциплине: «Информатика»

на тему:

«Разработка алгоритмов и программ решения алгебраических задач

численными методами»

Вариант № 40

Выполнил: студент группы 110Б Влад Андреев

Проверила: Кошелькова Л.В.

Москва 2016

Содержание

1. Условие задачи (Вариант 40)................…..……………………...………………..3

2. Анализ задания……………………………………………….………….…..…….3

3. Теоретические сведения………………………….…………………….…..……..4

4. Схемы алгоритмов и форма Delphi-приложения…………………………...…...6

5. Текст программы на языке программирования Delphi и результаты ее выполнения………………………………………...…………………...…….…..16

6. Набор тестов…………………………………………………………….......……22

7. Выводы…...………………………………………….……………………...…….25

8. Список использованной литературы……………………….…………..………26

1. Условие задачи

Разработать схему алгоритма и программу вычисления таблицы значений функции при заданных значениях аргумента и параметров.

Функция:

Параметр А принимает значения от An до Аk с шагом Dx.

Аргумент X принимает N значений от Xn с шагом Dx.

Параметр B равен значению корня уравнения, вычисленному в пределах от c до d с погрешностью Eps.

Уравнение:

2. Анализ задания

Входными данными в этой задаче являются:

• An – начальное значение параметра

• Ak – конечное значение параметра

• Da – шаг, с которым изменяется параметр

• Xn – начальное значение аргумента

• Dx – шаг значений аргумента

• N – количество значений аргумента

Для вычисления корня уравнения используются

следующие входные данные:

• c – нижняя граница области интегрирования

• d – верхняя граница области интегрирования

• Eps – погрешность вычисления

• Km – предельное число итераций

Выходными данными являются:

• Массив значений параметра Ma

• Массив значений аргумента Mx

• Массив значений функций My

В соответствии с принципами структурного программирования

в алгоритме присутствуют подпрограммы:

• Очистка таблицы значений функции и графика от результатов предыдущих вычислений (ClearRez)

• Вычисление корня уравнения (BFind)

• Табулирование функции (Tab)

• Обработка возможных ошибок (ProcErrorHappened)

3. Теоретические сведения

Метод трапеций для оценки определенного интеграла.

Величина определенного интеграла численно равна площади фигуры, образованной графиком функции и осью абсцисс (геометрический смысл определенного интеграла).

Следовательно, найти интеграл  – это значит оценить площадь фигуры, ограниченной перпендикулярами, восстановленными к графику подынтегральной функции  f(x)  из точек a и b, расположенных на оси аргумента x.

Для решения задачи разобьем интервал [a, b] на n одинаковых участков. Длина каждого участка будет равна h=(b-a)/n (см. рис.).

Восстановим перпендикуляры из каждой точки до пересечения с графиком функции f(x). Если заменить полученные криволинейные фрагменты графика функции отрезками прямых, то тогда приближенно площадь фигуры, а следовательно и величина определенного интеграла оценивается как площадь всех полученных трапеций. Обозначим последовательно значения подынтегральных функций на концах отрезков f₀, f₁, f₂,..., f_n и подсчитаем площадь трапеций

В общем случае формула трапеций принимает вид

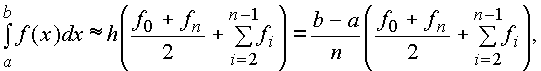
где f_i – значение подынтегральной функции в точках разбиения интервала (a,b) на равные участки с шагом h; f₀, f_n – значения подынтегральной функции соответственно в точках a и b.

Остаточный член пропорционален длине интервала [a,b] и квадрату шага h

Согласно рис. и формуле остаточного члена, точность вычисления определенного интеграла повышается с уменьшением шага h(увеличением числа отрезков n).

Метод трапеций можно реализовать в виде процедуры или даже функции, поскольку результат вычисления определенного интеграла – скалярная величина. Параметрами программного модуля являются границы интервала (a и b) и число шагов разбиения на малые интервалы n.