Добавил:

MrKOT1212 ikot.chulakov@gmail.com Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Самарский национальный исследовательский университет им. ак. С.П. Королёва (бывш. СГАУ, СамГУ)

Предмет:

Сопротивление материалов

Файл:

Методички для олимпийцев / Изд вар Сборник задач Всероссийских олимпиад

.pdf

Скачиваний:

Добавлен:

12.07.2020

Размер:

1.46 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1713 14 15 16 17 > Следующая >>>

РЕШЕНИЕ

Рассмотрим коромысло отдельно от остальной конструкции, заменяя взаимное действие друг на друга реактивными силами R1, R2

(рис. 10.4 Р, а):

		В			б)	х	l				•
a)							l
a)						• С GJp					х D
А		R2		3GJp	М1	• С GJp					х D
А	R1			3GJp	М1		Мк2			М2
	R1	R2	l	l	М1х		•	х		• М2
	В		l	l	в)	•	х	•		х
А	R1	l GJp l		г)	В	v	д)		В′		l
				2v	В	v		v	2φφ		l
					В′		A,B
								v2			l
				A					A′		l
				Рис. 10.4 Р					A′
				Рис. 10.4 Р

3GJp

•Мк1

C,D

Сумма моментов для коромысла относительно его опоры позволяет связать неизвестные реактивные силы:

2 R1 R2		3 M		R2		3 M	2 R1 .
		l				l

Реактивные силы оказывают на рассматриваемый вал воздействие в виде крутящих моментов:

M 1 R1 l,

M 2 R2 l

M 2 3M 2 R1 l 3M 2 M 1 ,

от которых на каждом участке возникают внутренние крутящие моменты:

М к1 M 1 M 2 3 M 1 3 M ,

М к2 M 1 .

Система один раз статически неопределима. Рассмотрим систему в деформированном состоянии (рис. 10.4 Р, б-в). Запишем два кинематических соотношения:

C 2 ,

C 2 D ,

распишем:

М к

M к

, тогда

3G J

G J

121

М к

M к

M к1

3 М к2

2 М к1 ,

3G J

G J p

3G J

3(3М1 3 М ) 3М1 0,

М1

М ,

М 2

3 М

М .

Следовательно:

М к1

9 M 3M

M ,

Мк 2

M ,

M l

3M l

v l ,

4G J

4G J р

Ответ: Угол поворота коромысла –

3M l

4G J р

10.5 Тонкостенная шарнирно-закреплённая обо-

лочка в форме усечённого конуса (рис. 10.5) нагре-

вается на t. Определить допускаемую степень на-

грева. Дано: α, E, R, σт, nт.

	2R	РЕШЕНИЕ
	2R	Применим метод сечений и рассмотрим равно-
	Рис. 10.5	Применим метод сечений и рассмотрим равно-
		весие конического элемента оболочки:

0 2 R cos m 2 r cos ,

0 m

r R ,

m r Rr 0 .

Записывая соотношение Лапласа для безмоментной теории оболочек:

m		t	p	,	m ,	p 0,	t 0 .
m
	t

Таким образом, напряжённое состояние одноосное и согласно закону Гука с учётом температурного расширения:

m Em t RE r0 t .

122

Из закрепления оболочки следует, что изменение длины образующей цилиндра l 0 , с другой стороны:

l m d s , где	d s	d r	– длина бесконечно малого элемента
		sin
L

образующей цилиндра, поэтому

2 R

R 0

d r

sin

E r

ln 2

0 ,

E sin

sin

Тогда m

E t

ln 2

R 0				t
		ln 2 R ln R sin			R
E sin
	0		E t	.

			ln 2

Согласно условию прочности:

mmax

T ln 2

E t nT

T ln 2

Ответ: Допускаемая степень нагрева – t

E t nT

10.6 Определить горизонтальное пере-

мещение торцевого сечения спиралевидного

бруса (рис. 10.6), нагруженного изгибающим

моментом. Дано: b, E, M, l >> b.

РЕШЕНИЕ

Для определения перемещений восполь-

зуемся интегралом Мора. Вначале получим

Рис. 10.6

зависимости изгибающих моментов в произ-

вольном сечении от действия прило-

женного момента M (рис. 10.6 Р)

Mи

y Mx

•My x

единичной

горизонтальной

силы,

приложенной также к торцевому се-

•

б)

чению. В произвольном сечении во

Mи=M х •

всех случаях нагружения имеет место

косой изгиб.

Рис. 10.6 Р

123

M x M cos , M y M sin ,

гх

z sin ,

гу

z cos .

Запишем интеграл Мора для определения горизонтального сме-

щения торцевого сечения, учитывая что

2 l

и d z

d :

M x

гx

M y M гy

4 M l 2

/ 2

d z

sin cos d .

E J x

E J y

J x

J y

Отдельно вычислим интеграл:

d cos 2

sin cos d 1

sin 2 d 1

/ 2

cos 2

cos 2 d

M l

Таким образом,

2 E

Вычислим:

b 4b 3

J x

4b b 3

b 4

J y

16b 4

Итак, окончательная величина искомого перемещения:

г	3 M l 2			1	1	0,448	M l 2	.

	2	E b	4		16		E b 4

Ответ: Горизонтальное перемещение торцевого сечения бруса –

г 0,448 M l 2 .

E b 4

2.18.Олимпиада 2011 г., г. Пермь, ПНИПУ

11.1Дан брус переменного сечения (рис. 11.1), нагруженный в центре силой F. В каком сечении стержня возникает максимальное по модулю нормальное напряжение?

124

l A

Рис. 11.1

РЕШЕНИЕ

Запишем уравнение равновесия (рис. 11.1 Р) RA + RC = F и условие совместности перемещений:

lA C =

lA B +

lB C =0

(1)

R d z

(R F ) d z

l AВ

, l BC

E A

( z )

E A( z )

d z

2l ln ( 2 z 2l ) .

A( z )

2 z 2l

RA	A
	A
l
F	B
F
l

Рис. 11.1 P

Поэтому из (1) имеем:

R A

2l ln ( 2 z 2l )

R A

2l ln ( 2 z 2l )

0 ,

E A

R A 2( ln1,5 ln 2)

( R A F ) 2( ln1 ln1,5) 0 ,

R A

ln 2 / 3

F 0,585 F ,

F R A 0,415 F .

ln 0,5

Таким образом, в сечении, принадлежащем участку АВ, чуть

выше точки приложения силы F:

(1)

0,585 F

0,390

(растяги-

1,5 A

вающее напряжение), а в точке C:

(2)

0,415 F

0,415

(сжимаю-

щее напряжение).

Следовательно, самое большое по модулю напряжение возника-

ет у нижней заделки стержня:

0,415

наиб

Ответ: максимальное нормальное напряжение –

0,415

наиб

возникает у нижней заделки стержня.

125

11.2 Имеется стержень с начальным несо-

вершенством,

выгнутый

по

дуге

окружности

ρ0

большого радиуса со стрелой прогиба в центре

v0 (рис. 11.2). Как необходимо нагреть стержень,

чтобы он стал прямым, если коэффициент тем-

пературного расширения равен α?

РЕШЕНИЕ

Рис. 11.2

Очевидно, стержень необходимо нагревать

неравномерно

по

ширине сечения.

Поскольку

равномерный

нагрев

не

влияет

на

кривизну

б)

стержня, нужно нагревать

ρ0

стержень следующим об-

разом (рис. 11.2 Р, а): вы-

пуклую часть не нагре-

вать,

вогнутую

нагревать на

Можно

Рис. 11.2 P

нагревать и обе поверхно-

сти с перепадом температур

На основании гипотезы плоских

сечений деформация вогнутого слоя равна ε = a/ρ, с другой сторо-

ны, деформация этого слоя равна ε =α

t. Тогда 1/ρ = α

t/a.

Исходную кривизну можно вычислить, зная длину стержня и

стрелу прогиба (рис. 11.2 Р, б):

АВС подобен

АВD, откуда полу-

чаем:

l / 2

, где ρ0 – исходный радиус кривизны. Так как

l / 2

0 v 0

v0 намного меньше, чем ρ0 , то

8v 0

l 2

Приравнивая начальную кривизну к температурной, получим

8v0

8a v0

l 2

Ответ: Чтобы стержень стал прямым, его вогнутую поверхность

необходимо нагреть на

8a v0 .

l 2

126

			11.3 При каких значениях	b
a) F	б)	F		a

			максимальное нормальное напряже-

bние в первом брусе станет больше, чем во втором (рис. 11.3)?

РЕШЕНИЕ

h	h
a	a

Рис. 11.3

приложена не в центре

Ми = Fb/2.

Первый брус подвержен внецентренному растяжению, а второй – центральному растяжению. В ослабленном сечении первого бруса сила сечения и создает изгибающий момент

	max			F		и		F		M и					F			F b / 2
	(1)																h ( a b ) 2 / 6
	(1)						A(1)			Wи				( a b ) h
							A(1)			Wи				( a b ) h
					F				3 F b					F		1		3
																				.
													2						2	.
			( a b ) h				h ( a b )						2			1		(1 )	2
			( a b ) h				h ( a b )							a h		1		(1 )
	max			F		F			1
	max			F		F			1
	(2)											.
	(2)					a h	1 2					.
		A( 2)				a h	1 2
Возьмем крайний случай (max1)														(max2) , тогда
	1				3				1		,
1		(1 ) 2					1 2				,
1		(1 ) 2					1 2
(1 ) (1 2 ) 3 (1 2 ) (1 ) 2 0,
5 2 2 0,												1 0,				2 2 / 5.

Нулевой корень не подходит по физическим соображениям, следовательно, при соотношении

2	(max1)	(max2) .
5

Ответ: Нормальное напряжение в первом брусе станет больше, чем во втором, при λ 2/5.

127

l	l
d	d
	2
p	Рис. 11.4

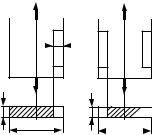
11.4 Дан двухступенчатый брус, защем- ленный по концам в заделках (рис. 11.4). Ле- вая часть бруса нагружена давлением p. Найти изменение объёма бруса.

РЕШЕНИЕ

Суммарная длина бруса не изменяется

l l 2	0,	(1)
но l (z1) l ,	l 2 (z2) l . Так как длины обоих участков оди-
наковы, то (z1)	(z2) .

Напряженное состояние в обеих частях стержня показано на рис.

11.4

Р, б-в. Из обобщённого закона Гука

( t r )

следует, что

(1)z

( p p )

(z1) 2 p

(z2 )

(z2 ) .

N б)

р в)

σz(1)

σz(2)

Рис. 11.4 Р

Учитываем,

что напряжения

от

реакций

заделках равны

(1)z

4 N

(z2)

. Подставляя деформации и напряжения в

d 2

4 N

уравнение (1), получим:

2 p

0 . Тогда внутрен-

няя

сжимающая

сила

равна

2 p d 2

напряжения:

2 p

(1)z

8 p

, (z2 )

Изменение объёма стержня выразим через объёмную деформацию

128

V V 2 V 2 0,

1 2 z

r , тогда

1 2

8 p

2 l

1 2

2 p

l .

2 p

Окончательно имеем: V

2 p l

(1 2 ) (10 16 ) .

20 E

Ответ: При нагружении левого участка давлением р объём бруса

уменьшается на V

d 2

p l

(1 2 ) (10 16 ) .

20 E

					11.5 Бесконечный стержень, имеющий
			K		плотность ρ, лежит на абсолютно жёстком
A		a	K	l	столе таким образом, что его конец выдви-
		a		l	нут за край стола на участок длиной l (рис.
	Рис. 11.5				нут за край стола на участок длиной l (рис.
	Рис. 11.5				11.5). Найти координату точки касания
стержня со столом a.					11.5). Найти координату точки касания
стержня со столом a.							а)
			РЕШЕНИЕ				а)	А	К
Можно считать, что стержень на-							б)		q a 2	q l 2
гружен распределённой нагрузкой q,							M		2	2
равной	произведению				плотности на			q а2	q l 2
площадь поперечного сечения (рис.								2	2
11.5 P, а). Очевидно, что в точке A, в							в)	а	1
которой		стержень		касается		стола	M1
Mx =	0,	так как кривизна стержня						Рис. 11.5 Р
						q l 2 .		Рис. 11.5 Р
равна нулю,			а в точке К – M x			q l 2 .
						2

Тогда эпюра моментов качественно выглядит так, как показана на рис. 11.5 P, б.

Найдём а из условия равенства нулю перемещения в точке K, при этом будем считать, что в точке А стержень закреплён в заделке

(рис. 11.5 P, в).

			1	q a 2	q l 2		1		1	q a 2		1
E J	x	K				a		a			a		a 0.
E J						a		a			a		a 0.
			2	2	2		3		3	2		4
			2	2	2		3		3	2		4

Откуда координата точки касания стержня со столом a 2 l .

129

Ответ: Координата точки касания стержня со столом – a 2 l .

b x

δa l

Рис. 11.6

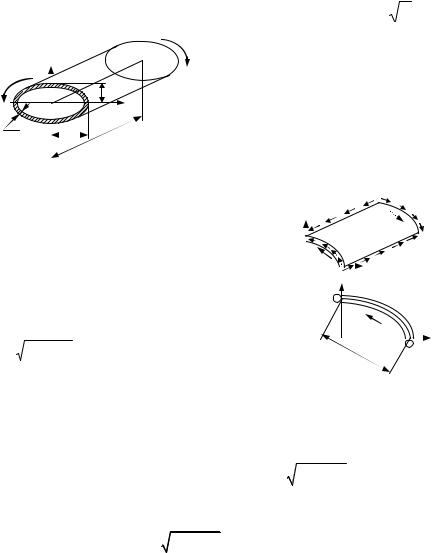
11.6 Тонкостенная трубка эллиптического поперечного сече-

Mния (δ << b) закручивается моментами M (рис. 11.6). Найти величину равнодействующей касательных напряжений в первой четверти сечения: х ≥ 0, у ≥ 0.

РЕШЕНИЕ

Как известно, касательные напряжения в тонкостенном замкнутом контуре при

кручении равны	M	M	M	.
		2 А*	2 a b
	Wк

Равнодействующую силу Р можно найти из уравнения равновесия моментов отсечённой части трубки (рис. 11.6 Р, б): P·l = F·h, где l – длина трубки,

h	a 2 b 2 – плечо силы F = τδl (рис.

11.6 Р, a), создаваемой касательными напряжениями τ, действующими в продольных сечениях трубки. Отсюда

	a)		Р
y			Р
	Р	х
	Р

	F •	у
	F •	у
б)		b Р			х
		a			х
		h		х
		h		F
				F
	Рис. 11.6 P

P	F h	l h	h .
P	l	l	h .
	l	l
В итоге получаем значение силы Р: P				M	a 2 b 2	.
В итоге получаем значение силы Р: P					2 ab	.
					2 ab

Ответ: Равнодействующая касательных напряжений в первой

четверти сечения – P	M	a 2 b 2	.
		2 a b

130

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1713 14 15 16 17 > Следующая >>>

Соседние файлы в папке Методички для олимпийцев

#
12.07.20203.05 Mб20Гафаров Опорный конспект.doc
#
12.07.2020202.28 Кб11Геометрич хар-ки Теория.docx
#
12.07.20201.46 Mб70Изд вар Сборник задач Всероссийских олимпиад.pdf
#
12.07.2020134.66 Кб8Метод жесткостей.doc
#
12.07.20202.24 Mб31Методика решения нест.doc
#
12.07.20202.42 Mб12Методика решения нест.pdf
#
12.07.20201.41 Mб18Несмеянов Метод.doc
#
12.07.2020358.43 Кб14Справочные данные2.pdf