1.4. Каноническая форма матричной записи злп и связанные с ней структуры данных и понятия линейного программирования

В матричном виде каноническая форма записи ЗЛП определятся следующим образом:

, , (1.37)

где - размерность ЗЛП по числу оптимизационных переменных;

- n-мерный вектор-столбец оптимизационных переменных;

- n-мерная вектор-строка коэффициентов целевой функции;

D – множество допустимых решений ЗЛП в n-мерном Евклидовом пространстве;

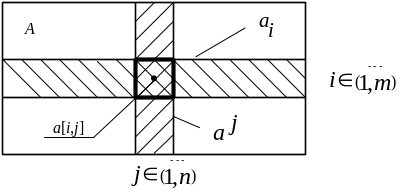
- - мерная матрица коэффициентов основных ограничений (матрица условий ЗЛП, рис.1.13).

Исходя из условий формирования ЗЛП и правил перехода к канонической форме записи, можно утверждать, что всегда . Крайний случай при совместной системе линейно независимых уравнений соответствует вырожденному случаю, когда ни о какой оптимизации (как о выборе лучшего решения из множества допустимых решений) речи не идет. Тогда решение ЗЛП – это просто решение системы линейных уравнений (конечно, если это решение существует и удовлетворяет условию ).

Для строк и столбцов матрицы условий будем использовать следующие обозначения:

- i-ая строка матрицы А, - j-ый столбец матрицы А;

- m-мерный вектор-столбец правых частей ограничений.

Базисом (B) ЗЛП с матрицей условий A_(mxn), имеющей ранг m, называется система из m линейно независимых векторов столбцов этой матрицы, расположенных в определенном порядке:

.

Для обозначения номера столбца здесь используется так называемая соподчиненная индексация, в которой j_i определяет номер столбца матрицы А, включенного в базис, а i - порядковый номер, определяющий положение этого столбца в базисе.

Например, при и для , , .

Если B определен, то ему в ЗЛП ставятся в соответствие следующие структуры данных:

- - базисное множество (система номеров столбцов матрицы А, или, что одно и то же, номеров оптимизационных переменных, включенных в определенном порядке в базис);

- В -квадратная m-мерная базисная матрица, составленная из базисных векторов–столбцов матрицы условий (ранг этой матрицы r(B)=m вследствие линейной независимости включенных в нее столбцов). Следовательно, для нее существует обратная матрица:

- B^-1 - обратная по отношению к В матрица (обратная базисная матрица), в которой

(В) - i-ая строка,

(В) - j-ый столбец,

(В)[i,j] - (i, j) – ый элемент;

- - m-мерная вектор-строка коэффициентов целевой функции при базисных переменных;

- А(В) - (m´n)–мерная матрица коэффициентов разложения векторов-столбцов матрицы условий A по векторам базиса:

. (1.39)

Мтрицы А(В) и А совпадают в только в том случае, когда В=Е.

Покажем, что это действительно так. Для произвольного l-ого вектора-столбца матрицы A(B) на основании соотношения (1.39) можно записать:

или, что одно и то же,

Таким образом, имеет место следующее важное и в дальнейшем широко используемое соотношение

, (1.40)

из которого и следует, что столбец состоит из коэффициентов разложения вектора-столбца a^l по векторам базиса.

Из (1.40) становится также очевидным, что для для векторов-столбцов , включенных в базис, соответствующие вектора и матрицы А(В)

(1.41)

где - вектор-столбец, у которого i-ая компонента равна единице, а остальные имеют нулевые значения, т.е. базисный вектор в разложении представляется только через самого себя.

Таким образом, из столбцов , располагая их в порядке, соответствующем базису, составляется единичная m – мерная матрица:

Кроме того, в линейном программировании используются следующие расширенные структуры данных:

- расширенная матрица условий ЗЛП. Ее размерность - (m+1,n);

- расширенный вектор-столбец правых частей ограничений размерности (m+1).

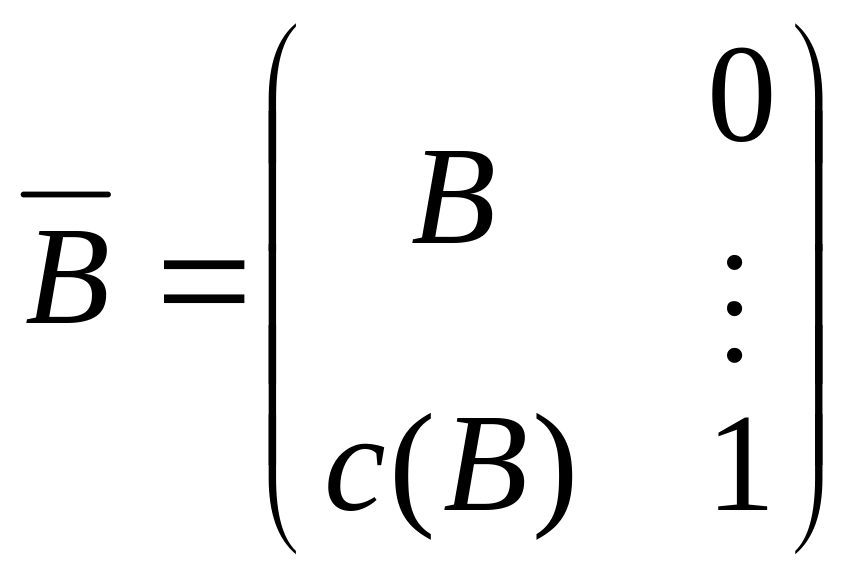- расширенная базисная матрица размерности (m+1)´(m+1);

• расширенная обратная базисная матрица:

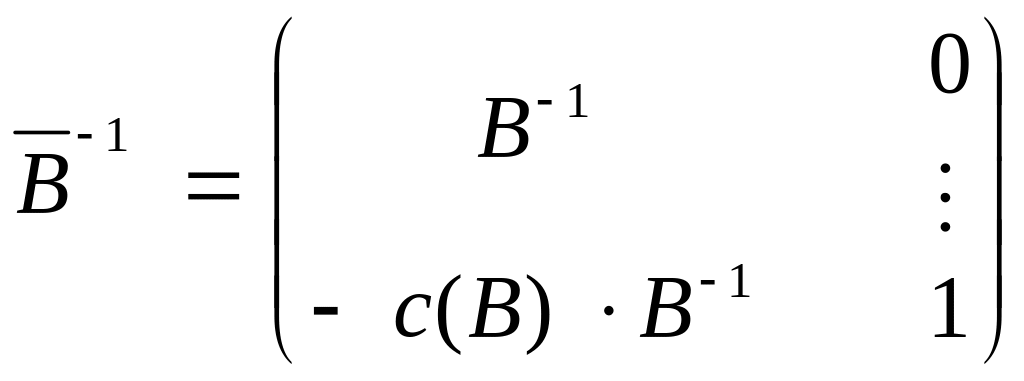
, (1.38)

вид которой получен из путем применения правил поблочного обращения. Для отдельных частей этой матрицы будем использовать следующие обозначения:

- i-ая строка (в частности, ,

- j-ый столбец,

- (i, j) – ый элемент;

- расширенная матрица :

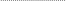. (1.42)

Для отдельных частей этой матрицы будем использовать следующие обозначения:

- i-ая строка,

- j-ый столбец,

- (i, j) – ый элемент.

Очевдны следующие соотношения:

; .

Видим, что - это (m+1)´n–мерная матрица. Ее верхняя часть представляет собой уже известную матрицу A(B), а последняя строка этой матрицы

(1.43)

в линейном программировании называется строкой симплекс-разностей.

Нетрудно увидеть,что

.

Для этой строки также будем использовать следующее обозначение , где симплекс-разность, соответствующая j-ому столбцу (j-ой переменной) ЗЛП в соответствии с (1.43) равна

(1.44)

Видим, что симплекс-разности зависят от базиса, для которого они определяются.

Сущность симплекс-разностей будет рассмотрена ниже при обосновании метода решения ЗЛП, называемого симплекс-методом.

Здесь необходимо сказать лишь о том, что симплекс-разности определяют скорость изменения целевой функции ЗЛП при определенном перемещении в пространстве оптимизационных переменных.