Лекция №2

1.2. Графическая интерпретация злп и связанные с этим понятия линейного программирования

Графически ЗЛП может быть представлена и решена лишь для случая двух оптимизационных переменных. Несмотря на такую малую размерность, рассмотрение графического изображения позволяет выявить многие характерные свойства ЗЛП произвольной размерности, связанные с ней понятия и определить стратегию работы алгоритма поиска её оптимального решения.

Рассмотрим задачу

, (1.14)

,

.

Использование здесь для обозначения типа ограничения условий , и говорит о том, что каждое конкретное (i-ое) ограничение может быть одного из этих типов. Приведенные здесь условия неотрицательности оптимизационных переменных являются в общем случае необязательными.

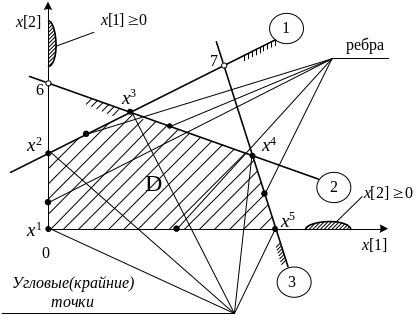
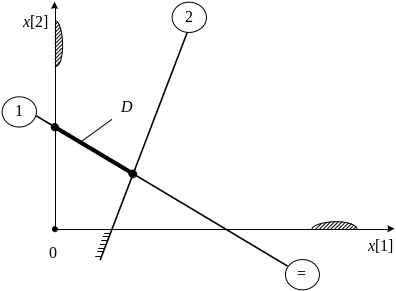
Графическое отображение D

Графическое отображение отдельного ограничения – прямой линией, для неравенств – со штриховкой наложенной в сторону полуплоскости, где неравенство выполняется.

Пересечение нескольких полуплоскостей образует множество допустимых решений D, представляющее собой выпуклый многогранник, ограниченный прямыми. Несложно себе представить, что в задаче с тремя переменными допустимое множество в общем случае будет не плоским, а объемным выпуклым многогранным множеством, ограниченным плоскостями. Строго показано, что в n-мерном случае множество D также представляет собой выпуклое многогранное множество, ограниченное гиперплоскостями.

Гиперплоскостью в n-мерном Евклидовом пространстве называется множество

. (1.15)

Угловой (крайней) точкой не пустого выпуклого многогранного множества в n-мерном Евклидовом пространстве называется такая его точка, которая образована пересечением гиперплоскостей, ограничивающих D.

Ребром не пустого выпуклого многогранного множества D в n-мерном Евклидовом пространстве называется такое его подмножество, которое образовано пересечением

n-1 гиперплоскостей, ограничивающих D. Геометрически – это всегда отрезки прямых линий, соединяющих соседние угловые точки.

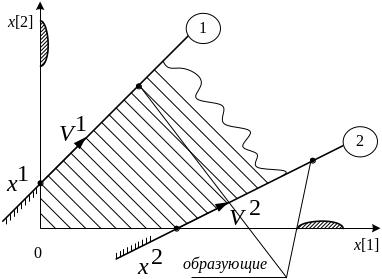
Образующей не пустого выпуклого многогранного множества D в n-мерном Евклидовом пространстве называется такое его ребро, которое имеет бесконечно удаленную точку. Уравнение образующей записывается в векторной форме следующим образом:

, (1.17)

где - угловая точка, являющаяся началом образующей;

- направляющий вектор образующей;

- скалярная величина, большая нуля, определяющая положение точки х.

Рис. 1.4	Рис. 1.5	Рис. 1.6
Рис. 1.7	Рис. 1.8	Рис. 1.9

1.2.2. Графическое представление целевой функции злп

Градиент целевой функции ЗЛП – это вектор, определяющий направление наибольшей скорости ее возрастания:

… , … , (1.18)

Градиент целевой функции ЗЛП не зависит от координат точки, в которой он вычислен.

Для ЗЛП с двумя переменными- это вектор с двумя компонентами:

.

Линия уровня целевой функции ЗЛП- это прямая, образованная целевой функцией при некотором заданном ее значении:

.

Она перпендикулярна направлению градиента целевой функции.