Механические колебания

 Кинематическое уравнение гармонических колебаний

,

Здесь х – смещение колеблющейся точки из положения равновесия;

t – время;

А – амплитуда колебаний;

ω – круговая (циклическая) частота колебаний;

– начальная фаза колебаний;

– фаза колебаний в момент t.

 Круговая (циклическая) частота колебаний:

, или ,

где и Т – частота (линейная частота) и период колебаний соответственно.

 Скорость точки, совершающей гармонические колебания:

.

 Ускорение колеблющейся точки при гармонических колебаниях:

.

 Период колебаний пружинного маятника (тела массой m, подвешенного на пружине жёсткостью k, рис. 1.16):

.

Формула справедлива для малых колебаний, пока выполняется закон Гука , и в пренебрежении массой пружины в сравнении с массой тела.

 Период колебаний математического маятника (материальной точки массой m, подвешенной на нерастяжимой невесомой нити длиной l, рис. 1.17):

,

где g – ускорение свободного падения.

 Период колебаний физического маятника (твёрдого тела, подвешенного в поле силы тяжести и способного колебаться относительно оси, не проходящей через центр масс, рис. 1.18):

.

Здесь J – момент инерции колеблющегося тела относительно оси колебаний, l – расстояние от центра масс маятника до оси (длина физического маятника), – приведённая длина физического маятника (то есть длина такого математического маятника, который имеет тот же период колебаний).

Ф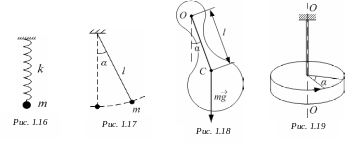 ормулы для периода колебаний физического и математического маятников справедливы при малых углах отклонения, когда можно положить . Для α=15⁰ ошибка в значении периода не превышает 1 %, а при α=3⁰ ошибка равна 0.005 %.

 Период колебаний крутильного маятника (тела, подвешенного на упругой нити, рис. 1.19):

,

где J – момент инерции тела относительно оси, совпадающей с нитью, – модуль кручения нити. Формула справедлива для упругих колебаний в пределах, в которых выполняется закон Гука: . Здесь M – момент упругой силы, возникающей при закручивании нити на угол .

 Полная энергия гармонического осциллятора:

 Закон сохранения энергии при гармонических колебаниях:

.

 Амплитуда А результирующего колебания , полученного при сложении двух колебаний одинаковой частоты, происходящих по одной прямой,

и

,

равна

,

г де А₁ и А₂ – амплитуды исходных колебаний; и – их начальные фазы (см. сложение колебаний по методу векторных диаграмм на рис. 1.20).

 Начальная фаза результирующего колебания при сложении однонаправленных колебаний:

.

 Уравнение траектории (рис. 1.21) точки, участвующей в двух взаимно перпендикулярных колебаниях одинаковой частоты,

и ,

с амплитудами А₁ и А₂ и начальными фазами и :

,

где – сдвиг фаз колебаний.

 Возвращающая (квазиупругая) сила, действующая на тело массой m при гармонических колебаниях:

,

где х – смещение колеблющейся точки из положения равновесия; ω – циклическая частота колебаний; – коэффициент пропорциональности. В частном случае пружинного маятника он равен жёсткости пружины.

 Дифференциальное уравнение гармонических колебаний

, или в стандартной форме:

,

где x – колеблющаяся величина; ω – круговая (циклическая) частота колебаний; – коэффициент квазиупругой силы.

 Дифференциальное уравнение затухающих колебаний

, или в стандартной форме:

,

где r – коэффициент сопротивления (коэффициент пропорциональности между силой сопротивления и скоростью: ); – коэффициент затухания; – круговая частота собственных (незатухающих) колебаний.

 Кинематическое уравнение затухающих колебаний (рис.1.22):

, или .

Здесь – круговая частота затухающих колебаний:

.

 Амплитуда затухающих колебаний:

,

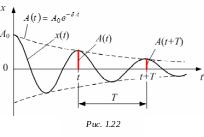где А₀ – амплитуда колебаний в момент t=0.

 Логарифмический декремент затухания равен по определению логарифму отношения амплитуд и двух следующих друг за другом колебаний, то есть колебаний, отстоящих во времени друг от друга на один период (рис. 1.22):

, или , или .

 Добротность

.

При условии (затухание мало):

.

Если , то добротность обратно пропорциональна относительному изменению энергии за один период:

.

 Дифференциальное уравнение вынужденных колебаний:

,

или в стандартной форме:

.

Здесь – вынуждающая сила (внешняя периодическая сила, действующая на колеблющуюся материальную точку и вызывающая вынужденные колебания); – её амплитудное значение; ω – её циклическая частота; ; – коэффициент затухания; – циклическая частота собственных (незатухающих) колебаний.

 Кинематическое уравнение вынужденных колебаний:

.

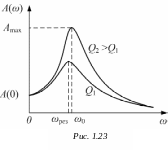 Амплитуда вынужденных колебаний как функция частоты (рис. 1.23):

.

 Начальная фаза вынужденных колебаний:

.

 Резонансная частота:

.

 Максимальная амплитуда (амплитуда при резонансе):

.

Волны

 Уравнение плоской волны, бегущей в положительном направлении оси OX (рис. 1.24):

,

где s – смещение частиц с координатой x из положения равновесия в момент времени t,

A – амплитуда,

ω – циклическая частота,

– волновое число (модуль волнового вектора),

– фазовая скорость (скорость распространения фиксированной фазы волны ),

– длина волны (расстояние, на которое распространяется волна за время, равное периоду колебаний),

– частота колебаний.

 Уравнение сферической волны:

,

Здесь s – смещение частиц с радиус-вектором из положения равновесия в момент времени t;

– волновой вектор, равный по величине , направленный вдоль луча;

– амплитуда сферической волны; r – расстояние до источника.

 Скорость распространения продольных и поперечных упругих волн в твёрдом теле:

, ,

где E – модуль Юнга, G – модуль сдвига, ρ – плотность.

 Скорость звука в газе:

,

где Т – абсолютная температура, R – универсальная газовая постоянная, μ – молярная масса газа, γ – показатель Пуассона (для воздуха ).

 Скорость распространения поперечной волны по струне:

,

где F – сила натяжения струны, S – площадь сечения струны, ρ – плотность.