Квантовые свойства света

 Полная энергетическая светимость (интегральная интенсивность теплового излучения) R_T численно равна энергии всех длин волн, излучаемой за единицу времени с единичной площади поверхности нагретого тела:

, или ,

где – мощность излучения (световой поток).

 Спектральная плотность энергетической светимости (монохроматическая интенсивность излучения) численно равна энергии, излучаемой за единицу времени с единичной площади поверхности тела в расчёте на единичный интервал длин волн вблизи заданной длины волны:

.

 Спектральная поглощательная способность тела – это величина, показывающая, какую долю энергии падающего излучения в интервале длин волн [ d] вблизи данной длины волны  тело поглощает:

.

Для абсолютно черного тела .

 Закон Кирхгофа: отношение монохроматической интенсивности излучения к поглощательной способности тела не зависит от природы тела; является универсальной (одинаковой для всех тел) функцией длины волны и температуры (универсальная функция Кирхгофа ):

.

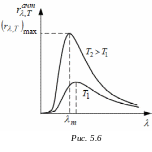
Для абсолютно чёрного тела (рис. 5.6):

.

 Первый закон Вина (закон смещения Вина). Длина волны λ_m, на которую приходится максимум монохроматической интенсивности излучения абсолютно чёрного тела, обратно пропорциональна абсолютной температуре (см. рис.5.6):

.

Здесь – первая константа Вина.

 Второй закон Вина: максимальное значение спектральной плотности энергетической светимости абсолютно чёрного тела прямо пропорционально пятой степени абсолютной температуры (см. рис. 5.6):

.

Здесь – вторая константа Вина.

 Закон Стефана-Больцмана. Полная энергетическая светимость абсолютно черного тела пропорциональна четвертой степени абсолютной температуры:

.

Здесь – постоянная Стефана-Больцмана.

 Полная энергетическая светимость серого тела

,

где – коэффициент черноты (коэффициент серости) серого тела, то есть тела, одинаково поглощающего излучение всех длин волн: для всех λ.

 Энергия фотона

, или , или .

Здесь – частота света; – круговая частота; – длина волны света; – скорость света в вакууме; – постоянная Планка; – редуцированная постоянная Планка (постоянная Планка «с чертой»).

 Масса фотона

.

 Импульс фотона

, или .

 Давление света при нормальном падении лучей

, или .

Здесь – энергетическая освещённость (энергия света, попадающая на единичную площадку за единицу времени); – коэффициент отражения, равный нулю для зачернённой поверхности и единице для зеркальной; – объёмная плотность энергии световой волны.

 Интенсивность света (плотность потока энергии) – это энергия световых волн, переносимая через единичную площадку, перпендикулярную лучам, за единицу времени:

.

 Уравнение Эйнштейна для внешнего фотоэффекта:

, или .

Здесь – энергия фотона, падающего на поверхность металла; – максимальная кинетическая энергия фотоэлектронов, – их скорость; – задерживающее напряжение; – работа выхода электрона из металла.

 Красная граница фотоэффекта – это минимальная частота или максимальная длина волны , при которых ещё возможен фотоэффект:

, или .

 Изменение длины волны при эффекте Комптона (упругом рассеянии фотона на свободном электроне):

.

Здесь – длина волны падающего (первичного) фотона, – длина волны рассеянного фотона, – угол рассеяния, m – масса электрона (или протона, если рассеяние происходит на протоне).

 Комптоновская длина волны:

.