
elm-02
.pdf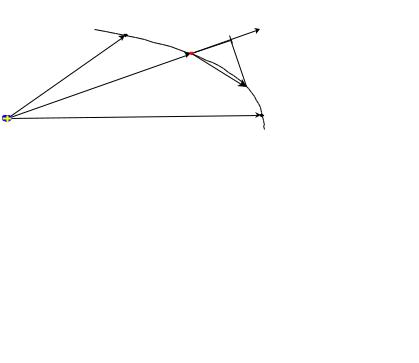
|
|
|
~ |
1 |
q′ |
d|~r| |
F |
|
|||
~r1 |
|
|
|
|
|
|
|
|
~r |
|
|
|
|
|
d~r |
|
|
|
2 |
|
|
|
~r2 |
• абота на элементарном пути d~r:
~ |
1 qq′ |
1 qq′ |
1 qq′ |
|||||||||
dA = F d~r = |
|
|
|
rd~r = |
|
|
|
rd|~r| = |
|
|
|
dr |
4πε0 |
r3 |
4πε0 |
r3 |
4πε0 |
r2 |
|||||||
• конечнойабота силыточкиКулоиíàå зависит толькоотормыотначальнойтраектории:
|
2 |
qq′ |
r2 |
|
qq′ |
|
qq′ |
|
A12 = |
~ |
|
dr |
= |
− |
|||
F d~r = |
4πε0 |
|
r2 |
4πε0r1 |
4πε0r2 |
|||
|
1 |
|
r1 |
|
|
|
|
|
точечÊóëэнергияПоïàáтенятиеîòàциальнаяîãîñèëûзаряда
системыЕдиницаизм рения ПотенциалСвязьнциалаз рядов напряж¼нностиïî ипотенциальны ЦиркуляциÝê рхности
вектора ~
E 14/34
|
|
|
~ |
1 |
q′ |
d|~r| |
F |
|
|||
~r1 |
|
|
|
|
|
|
|
|
~r |
|
|
|
|
|
d~r |
|
|
|
2 |
|
|
|
~r2 |
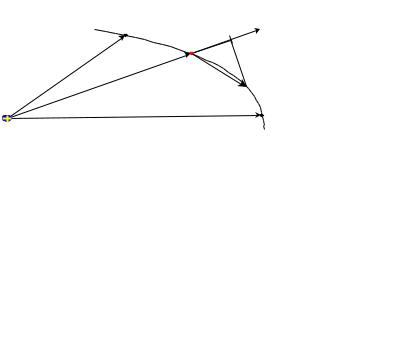
• абота на элементарном пути d~r:
~ |
1 qq′ |
1 qq′ |
1 qq′ |
|||||||||
dA = F d~r = |
|
|
|
rd~r = |
|
|
|
rd|~r| = |
|
|
|
dr |
4πε0 |
r3 |
4πε0 |
r3 |
4πε0 |
r2 |
|||||||
• конечнойабота силыточкиКулоиíàå зависит толькоотормыотначальнойтраектории:
|
2 |
qq′ |
r2 |
|
qq′ |
|
qq′ |
|
A12 = |
~ |
|
dr |
= |
− |
|||
F d~r = |
4πε0 |
|
r2 |
4πε0r1 |
4πε0r2 |
|||
|
1 |
|
r1 |
|
|
|
|
|
точечÊóëэнергияПоïàáтенятиеîòàциальнаяîãîñèëûзаряда
системыЕдиницаизм рения ПотенциалСвязьнциалаз рядов напряж¼нностиïî ипотенциальны ЦиркуляциÝê рхности
вектора ~
E 14/34

•тсоваåршаемаяктор и. им работа не зависит от ормы
•представаботу èлтьконсервативкак изменеíогоие потенциальнойполя можно энергии:
|
qq′ |
qq′ |
|
|
A12 = |
|
− |
|
= W1 − W2 |
4πε0r1 |
4πε0r2 |
|||
• Потенциальная энергия заряда q′ в поле заряда q:
qq′
W = 4πε0r + const
• Положимудалениипри constíà=бесконечность0. Тогда потенциобрàльнаящаетсяэнергиявнуль.
точечÊóëэнергияПоïàáтенятиеîòàциальнаяîãîñèëûзаряда
системыЕдиницаизм рения ПотенциалСвязьнциалаз рядов напряж¼нностиïî ипотенциальны ЦиркуляциÝê рхности
вектора ~
E 15/34

• совпредставаботуршаемаяктор и. им работа не зависитпотенциальнойормы
• |
ñèлтьконсервативкак изменеíогоие поля можно энергии: |
||||
|
|
qq′ |
qq′ |
|
|
|
A12 = |
|
− |
|
= W1 − W2 |
|
4πε0r1 |
4πε0r2 |
|||
• |
Потенциальная энергия заряда q′ в поле заряда q: |
||||
qq′
W = 4πε0r + const
• Положимудалениипри constíà=бесконечность0. Тогда потенциобрàльнаящаетсяэнергиявнуль.
точечÊóëэнергияПоïàáтенятиеîòàциальнаяîãîñèëûзаряда
системыЕдиницаизм рения ПотенциалСвязьнциалаз рядов напряж¼нностиïî ипотенциальны ЦиркуляциÝê рхности
вектора ~
E 15/34
• совпредставаботуршаемаяктор и. им работа не зависитпотенциальнойормы
• |
ñèлтьконсервативкак изменеíогоие поля можно энергии: |
||||
|
|
qq′ |
qq′ |
|
|
|
A12 = |
|
− |
|
= W1 − W2 |
|
4πε0r1 |
4πε0r2 |
|||
• |
Потенциальная энергия заряда q′ в поле заряда q: |
||||
qq′
W = 4πε0r + const
• Положимудалениипри constíà=бесконечность0. Тогда потенциобрàльнаящаетсяэнергиявнуль.
точечÊóëэнергияПоïàáтенятиеîòàциальнаяîãîñèëûзаряда
системыЕдиницаизм рения ПотенциалСвязьнциалаз рядов напряж¼нностиïî ипотенциальны ЦиркуляциÝê рхности
вектора ~
E 15/34
• совпредставаботуршаемаяктор и. им работа не зависитпотенциальнойормы
• |
ñèлтьконсервативкак изменеíогоие поля можно энергии: |
||||
|
|
qq′ |
qq′ |
|
|
|
A12 = |
|
− |
|
= W1 − W2 |
|
4πε0r1 |
4πε0r2 |
|||
• |
Потенциальная энергия заряда q′ в поле заряда q: |
||||
qq′
W = 4πε0r + const
• Положимудалениипри constíà=бесконечность0. Тогда потенциобрàльнаящаетсяэнергиявнуль.
точечÊóëэнергияПоïàáтенятиеîòàциальнаяîãîñèëûзаряда
системыЕдиницаизм рения ПотенциалСвязьнциалаз рядов напряж¼нностиïî ипотенциальны ЦиркуляциÝê рхности
вектора ~
E 15/34
• |
величинупотенциальнэтогоойую энергиизарядаэнергиюоста¼тся.пробногоНо′ отношение′′ постоянным:заряда на |
q q |
ϕ = W
Этаэлектрическоговеличина называетсяполя. потенциаломq′
•Потенциал поля точечного заряда:
1 q
ϕ= 4πε0 r
точечÊóëэнергияПоïàáтенятиеîòàциальнаяîãîñèëûзаряда
системыЕдиницаизм рения ПотенциалСвязьнциалаз рядов напряж¼нностиïî ипотенциальны ЦиркуляциÝê рхности
вектора ~
E 16/34
• |
величинупотенциальнэтогоойую энергиизарядаэнергиюоста¼тся.пробногоНо′ отношение′′ постоянным:заряда на |
q q |
ϕ = W
Этаэлектрическоговеличина называетсяполя. потенциаломq′
•Потенциал поля точечного заряда:
1 q
ϕ= 4πε0 r
точечÊóëэнергияПоïàáтенятиеîòàциальнаяîãîñèëûзаряда
системыЕдиницаизм рения ПотенциалСвязьнциалаз рядов напряж¼нностиïî ипотенциальны ЦиркуляциÝê рхности
вектора ~
E 16/34

Потенциал |
точечКулабîòàîãîñèëûзаряда |
|
òå |
||
|
энергия |
|
я в очке численно равен потенц альной энергии, |
Ïîнятие |
|
Единица |
||
к т рой обладает в этой точке единичный |
||
ïîëожительный заряд. |
изм рения |
|
ï циальная |
||
|
системы з рядов |
ПотенциалСвязьнапряж¼нностиипотенциальнынциала ïîЭк рхности Циркуляци
вектора ~
E 17/34

• |
|
ϕ |
точеч ого заряда |
|
|
|
|
||
|
W = qϕ |
|
àá |
ñèëû |
|
|
Култеîòà |
||
• абота по перемещению заряда равна: |
|
|||
|
энергия |
|||
|
|
|
Ïîнятие |
|
ãäå |
A12 = q(ϕ1 − ϕ2) = −q ϕ, |
|
Единица |
|
|
|
|
изм рения |
|
|
|
|
ï |
циальная |
|
ϕ = ϕ2 − ϕ1. |
|
системы з рядов |
|
• Если заряд переместили на бе конечнос ь, то |
|
|||
|
Связь |
|||
|
|
|
||
φ2 = 0 (мы договорились так ñчитать), òî |
|
напряж¼нности |
||
|
|
нциала |
||
|
A∞ = qϕ |
|
Эк ипотенциальны |
|
|
|
Потенциалïî |
||
|
|
|
Циркуляцирхности |
|
вектора ~
E 18/34
