
- •Лекции по курсу
- •1. Общие сведения
- •1.1 Типы квантования непрерывных сигналов.
- •1.2. Решетчатые функции разностные уравнения.
- •1.3. Обобщенная структурная схема дискретной системы.
- •1.4. Простейший импульсный элемент. Формирующий элемент. Фиксатор.
- •2. Основы теории z-преобразования
- •2.1. Дискретное преобразование Лапласа. Z-преобразование.
- •2.2. Основные теоремы z-преобразования.
- •2.3. Передаточная функция разомкнутой дискретной системы.
- •2.4. Последовательное соединение звеньев в дискретных сау.
- •2.5. Передаточная функция замкнутой дискретной системы.
- •2.6. Обратное z-преобразование.
- •3. Анализ устойчивости и точности
- •3.1 Прямой метод оценки устойчивости.
- •3.2 Критерий устойчивости Шур-Кона.
- •3.3 Критерий устойчивости, использующий билинейное преобразование.
- •3.4. Абсолютно устойчивые системы.
- •3.5. Анализ точности дискретных систем.
- •4. Частотные характеристики дискретных систем
- •4.1. Теорема Котельникова-Шеннона.
- •4.2. Логарифмические частотные характеристики дискретных сау.
- •5. Определение реакции дискретной сау
- •5.1. Метод дробного квантования.
- •5.2. Метод модифицированного z-преобразования.
- •6. Системы автоматического управления
- •6.1. Структура системы.
- •6.2. Передаточные функции цву, реализующего типовые законы управления.
- •7. Коррекция цифровых систем управления
- •7.1. Коррекция дискретных сау с помощью непрерывных регуляторов.
- •7.2. Коррекция сау с помощью цифровых регуляторов.
- •7.3. Физическая реализуемость цифровых регуляторов.
- •7.4. Реализация цифровых регуляторов импульсными фильтрами.
- •7.5. Реализация цифровых регуляторов на базе цву.
- •8. Методические указания и вариаты расчетно-графического задания
- •90 20 0 0 -90 -20 -180 -40 -270 -60 20 2 1
8. Методические указания и вариаты расчетно-графического задания
Целью курсовой работы является закрепление теоретического материала дисциплины “Дискретные системы”. В процессе выполнения работы студенты получают определенные практические навыки расчета дискретных систем, осуществляют выбор наиболее приемлемых методов их анализа и синтеза.
Выбор варианта
На рис. 52-54 приведены структурные схемы нескорректированных дискретных систем автоматического регулирования (САР). Численные значения параметров звеньев, входящих в приведенные системы, указаны в таблице 1.
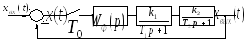
Рис. 52Структурная схема нескорректированной
дискретной САУ
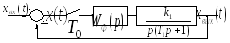
Рис. 53Структурная схема нескорректированной
дискретной САУ
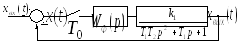
Рис. 54Структурная схема нескорректированной
дискретной САУ
Таблица 1
Численные значения параметров звеньев нескорректированной САУ
-
Номер
варианта
Структура
схемы
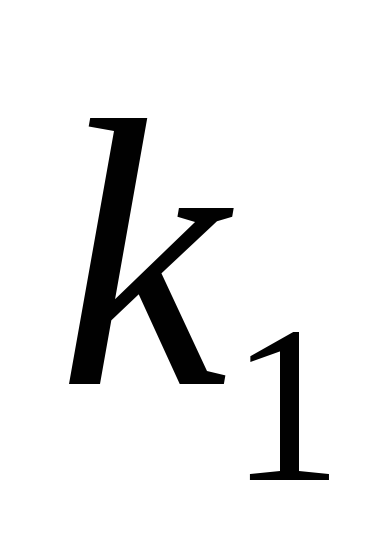
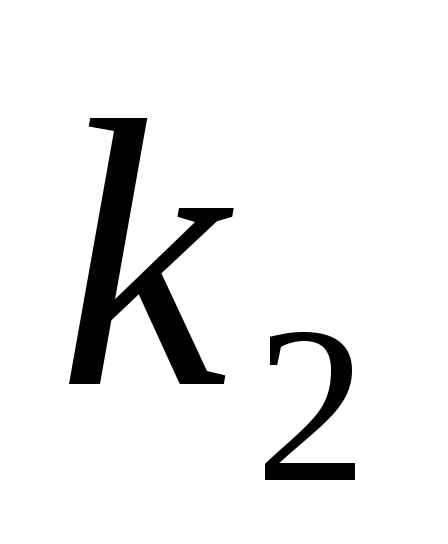
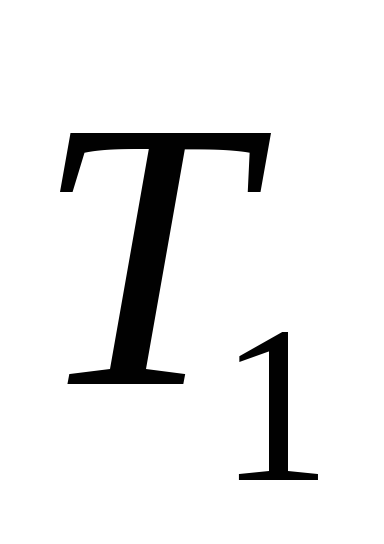
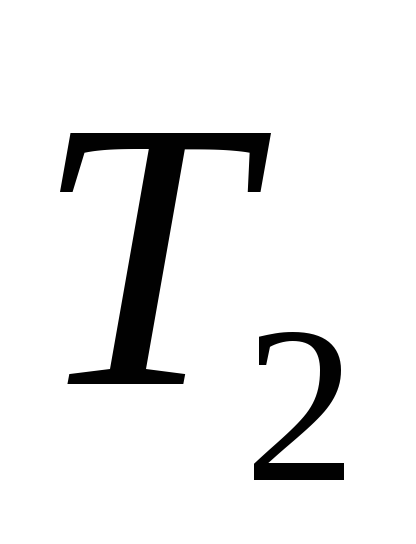
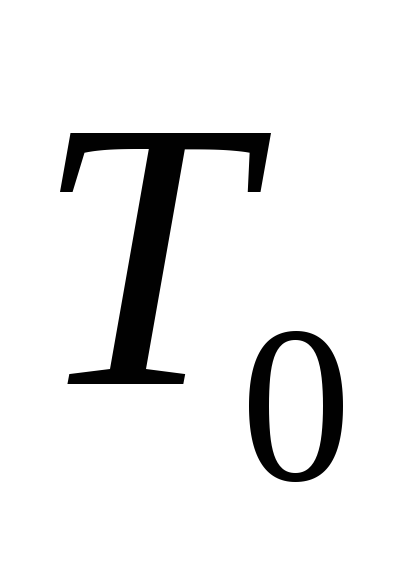
0
Рис. 52
5
1
0,5
1
0,1
1
Рис. 53
2
-
1
-
0,5
2
Рис. 54
5
-
0,6
0,6
0,4
3
Рис. 52
4
5
0,6
1,5
0,2
4
Рис. 53
1
-
0,5
-
0,1
5
Рис. 54
2
-
0,8
0,4
0,2
6
Рис. 52
2
4
0,4
0,5
0,1
7
Рис. 53
5
-
0,5
-
0,2
8
Рис. 54
1
-
2
1
0,4
9
Рис. 52
1
8
0,5
0,4
0,2
10
Рис. 53
10
-
0,2
-
0,1
11
Рис. 54
2
-
0,4
0,2
0,2
12
Рис. 52
4
4
1
0,5
0,5
13
Рис. 53
8
-
0,4
-
0,2
14
Рис. 54
2
-
1
0,6
0,5
15
Рис. 52
4
1
2
5
0,4
16
Рис. 53
12
-
0,4
-
0,2
17
Рис. 54
2
-
0,4
0,2
0,1
Задание
Определить передаточную функцию
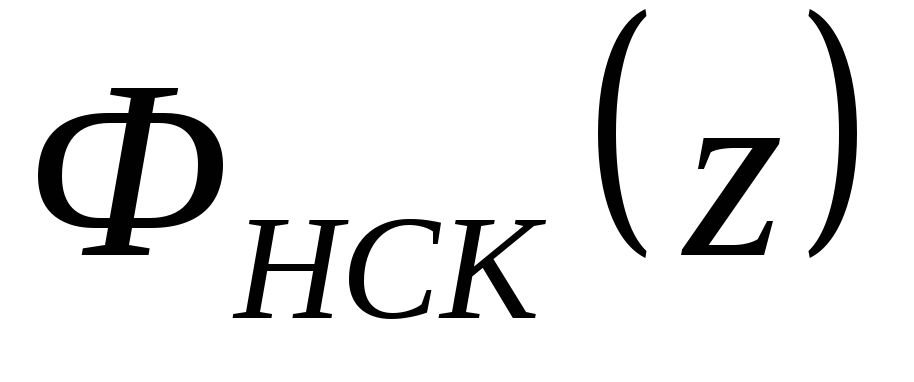 и модифицированную функцию
и модифицированную функцию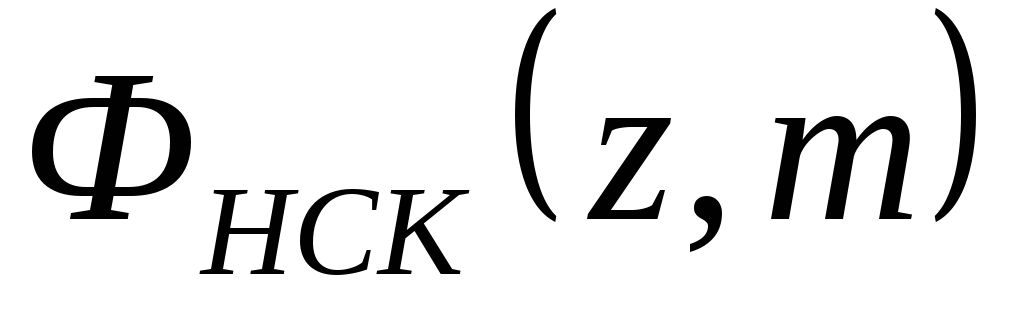 замкнутой нескорректированной системы.
замкнутой нескорректированной системы.Оценить устойчивость нескорректированной системы прямым методом и используя критерии устойчивости.
Определить начальное и установившееся (для устойчивых систем) значения решетчатой функции
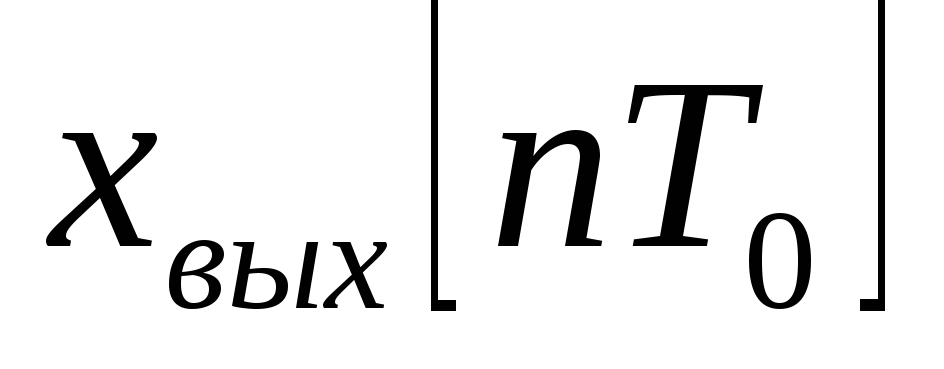 .
.Найти выражения для решетчатой функции
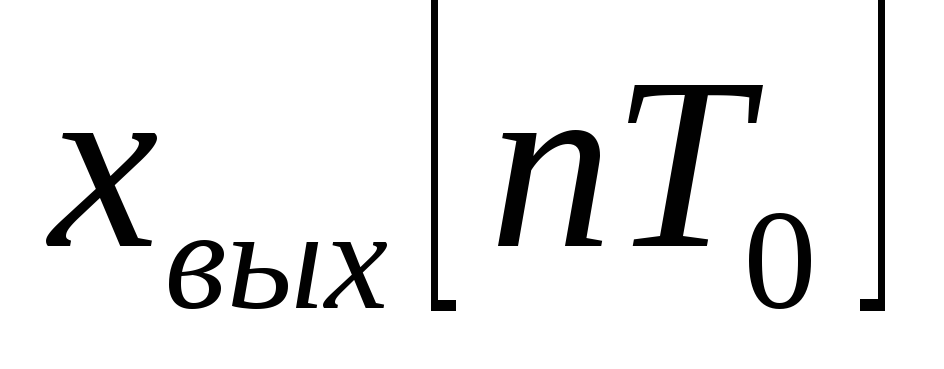 и модифицированной решетчатой функции
и модифицированной решетчатой функции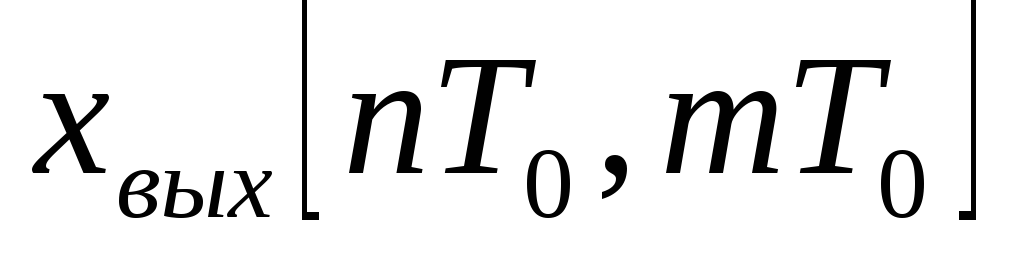 .
Построить графики этих функций на
временном интервале
.
Построить графики этих функций на
временном интервале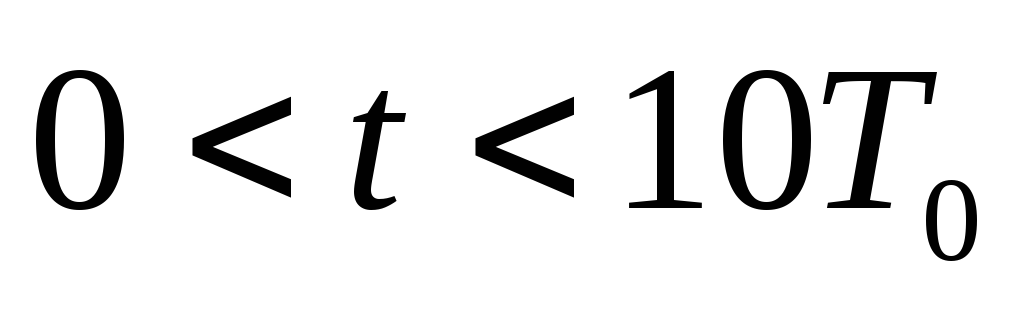 .
.Построить логарифмические амплитудно- и фазочастотные характеристики разомкнутой нескорректированной системы в функции абсолютной псевдочастоты
 .
.Определить передаточную функцию непрерывного корректирующего звена
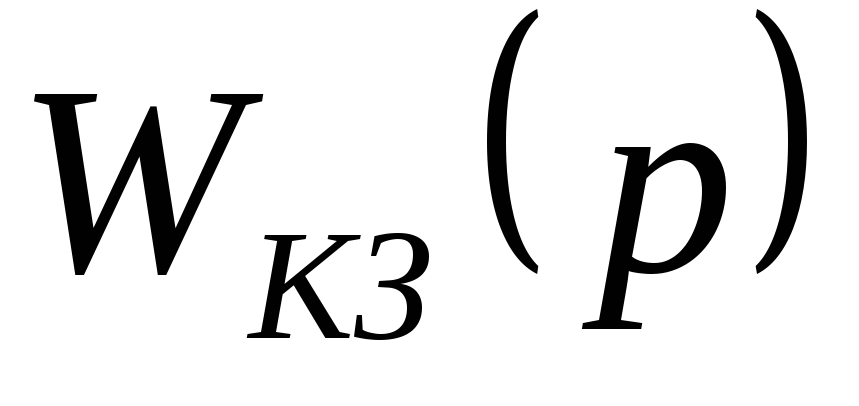 .
Привести его схему, рассчитать параметры.
.
Привести его схему, рассчитать параметры.Определить передаточную функцию дискретного корректирующего звена
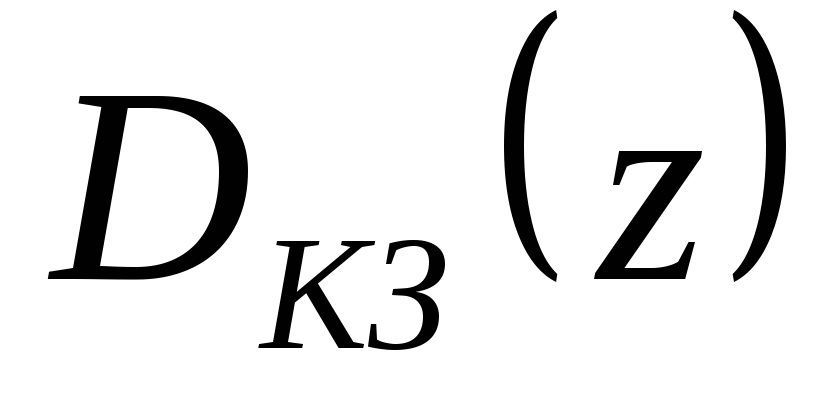 .
.Для случая реализации
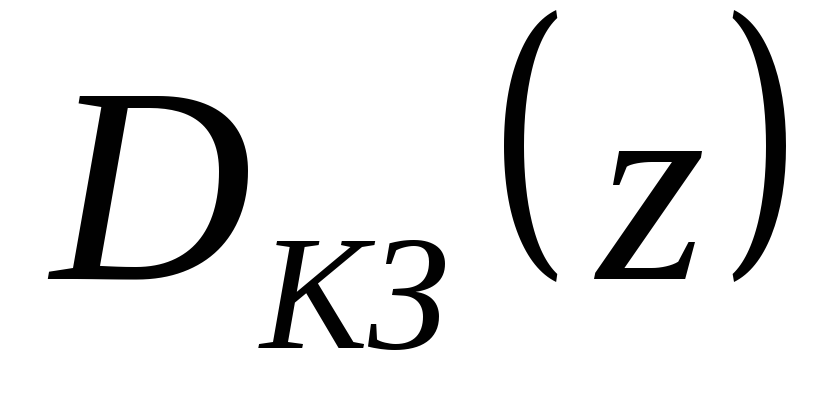 с помощью цифрового вычислительного
устройства разработать структуру
программы, привести рекуррентные
выражения для расчета текущих значений
выходного сигнала устройства.
с помощью цифрового вычислительного
устройства разработать структуру
программы, привести рекуррентные
выражения для расчета текущих значений
выходного сигнала устройства.Для случая реализации
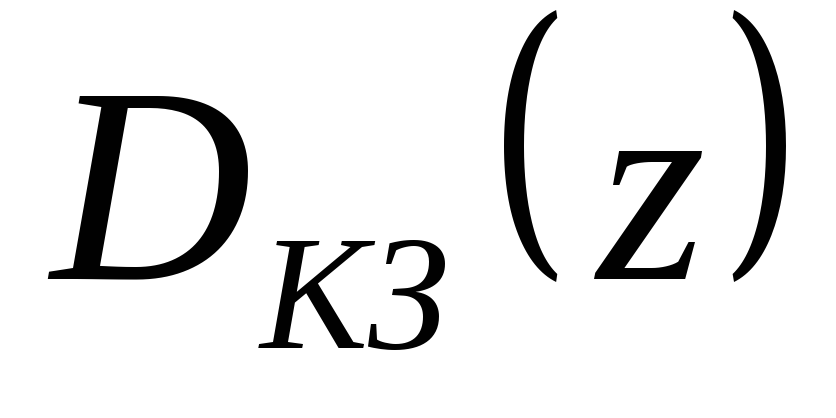 с помощью импульсного фильтра определить
передаточную функцию корректирующего
четырехполюсника, привести его схему,
рассчитать параметры.
с помощью импульсного фильтра определить
передаточную функцию корректирующего
четырехполюсника, привести его схему,
рассчитать параметры.Осуществить моделирование нескорректированной и скорректированной САР с использованием программы PSM. Результаты моделирования привести в отчете.
Примечание 1. При выполнении всех пунктов « Задания » считать, что на вход системы подан единичный ступенчатый сигнал.
Примечание 2. При выполнении пунктов 6,7,8,9 « Задания » необходимо обеспечить следующие показатели качества регулирования:
-время регулирования
процесса_________________________________________![]()
-перерегулирование
![]() ________________________________________________
________________________________________________![]()
-величина установившейся статической
ошибки___________________________![]()
Методические указания
Конечная цель выполненной работы состоит в синтезе САР, удовлетворяющей ряду требований к показателям качества регулирования системы. Указанная цель является достигнутой, если определены структура и параметры корректирующего устройства, обеспечивающего достаточно хорошее приближение характеристик системы к желаемым. Кроме указанных в « Задании » требований к статической точности, времени регулирования и перерегулирования, при синтезе корректирующих устройств дискретных САР можно задаваться и другими критериями, например желаемым характером реакции системы на определенное входное воздействие или условием конечной длительности переходного процесса.
В отличие от непрерывных САР в дискретных системах применяют два способа коррекции – непрерывный и дискретный. При первом способе коррекция осуществляется введением в систему непрерывных (аналоговых) корректирующих устройств, при втором – введением импульсных фильтров или цифровых регуляторов.
Реализуем указанные способы применительно к системе, соответствующей нулевому варианту «Задания». Для достижения приемлемой точности результатов при всех вычислениях необходимо учитывать не менее трех значащих цифр.
Передаточная функция разомкнутой нескорректированной системы при наличии в ней фиксатора в качестве формирующего элемента определяется следующим образом:
![]()
где
![]() -
передаточные функции непрерывной части
разомкнутой системы и фиксатора
соответственно.
-
передаточные функции непрерывной части
разомкнутой системы и фиксатора
соответственно.
Для рассматриваемой САР:
![]()
Передаточная и модифицированная передаточные функции замкнутой нескорректированной системы вычисляются по формулам:
![]() и
и![]()
где![]() -
передаточная и модифицированная
передаточная функции прямой цепи САР.
Для систем с единичной обратной связью
-
передаточная и модифицированная
передаточная функции прямой цепи САР.
Для систем с единичной обратной связью![]() и
и![]() совпадают.
совпадают.
Для рассматриваемой системы:
![]() ;
;
![]() ;
;
где:
![]()
![]()
![]()
Передаточная функция
![]() может быть получена из выражения для
может быть получена из выражения для![]() :
:
![]()
Зная выражения для
![]() и
и![]() ,
можно записать
,
можно записать![]() -изображения
реакции системы на единичное ступенчатое
воздействие:
-изображения
реакции системы на единичное ступенчатое
воздействие:
![]()
2. Корни характеристического уравнения замкнутой нескорректированной системы, рассматриваемой в качестве примера, равны:
![]()
Модуль корней равен
![]() ,
т.е. корни лежат внутри единичной
окружности с центром в начале координат
комплексной плоскости
,
т.е. корни лежат внутри единичной
окружности с центром в начале координат
комплексной плоскости![]() .
Следовательно, система устойчива.
.
Следовательно, система устойчива.
Аналогичный вывод может быть сделан,
если для оценки устойчивости использовать
билинейное преобразование. После
подстановки
![]() характеристическое уравнение замкнутой
системы примет вид:
характеристическое уравнение замкнутой
системы примет вид:
![]()
При использовании указанного преобразования условия устойчивости непрерывных и дискретных систем совпадают, в следствии чего совпадают и методы оценки устойчивости. Так, согласно критерию Рауса-Гурвица необходимым и достаточным условием устойчивости САУ второго порядка является положительность коэффициентов характеристического уравнения. Это условие для рассматриваемой системы выполняются.
Начальное и установившееся значения решетчатой функции
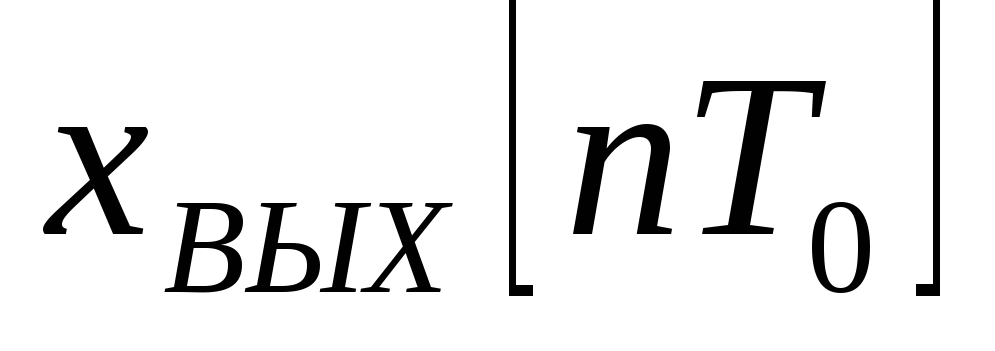 определяются по
определяются по -
изображению
-
изображению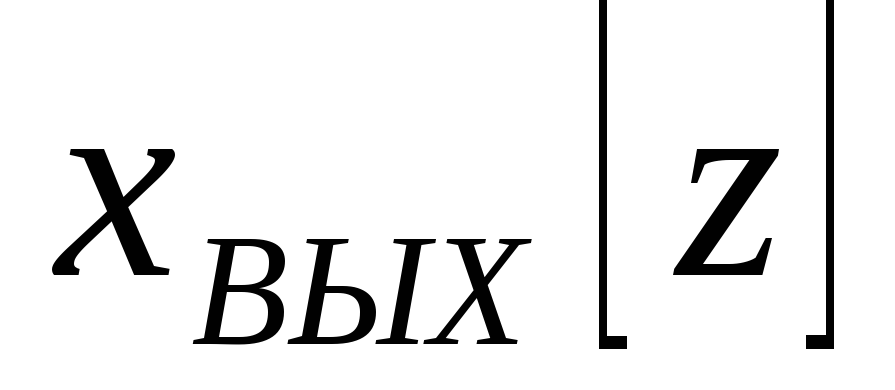 на основании соответствующих теорем
на основании соответствующих теорем -
преобразования:
-
преобразования:
![]() ;
(62)
;
(62)
![]() (63)
(63)
причем (63)
справедливо при условии, что выражение
![]() не имеет полюсов за пределами окружности
единичного радиуса и на самой окружности
с центром в начале координат комплексной
плоскости
не имеет полюсов за пределами окружности
единичного радиуса и на самой окружности
с центром в начале координат комплексной
плоскости![]() .
.
Если выходной сигнал системы представляет собой реакцию на единичное ступенчатое воздействие, то (62)-(63) могут быть преобразованы к виду:
![]() ;
;![]()
Для определения искомых значений
решетчатой функции можно воспользоваться
и модифицированным
![]() -
изображением
-
изображением![]() .
В этом случае соответствующие выражения
имеют вид:
.
В этом случае соответствующие выражения
имеют вид:
![]() ;
;
![]() ;
;
Для рассматриваемой системы:
![]()
Из последнего следует, что установившаяся ошибка системы равна 0,163.
Для большинства реальны дискретных САУ порядок числителя
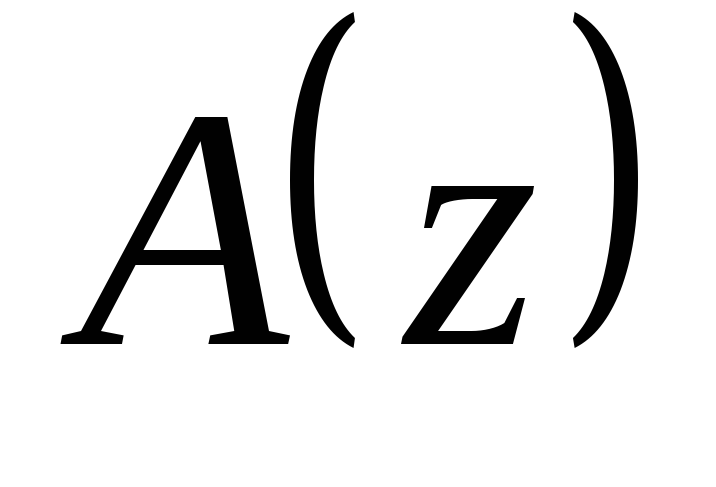 передаточной функции замкнутой системы
ниже порядка ее знаменателя
передаточной функции замкнутой системы
ниже порядка ее знаменателя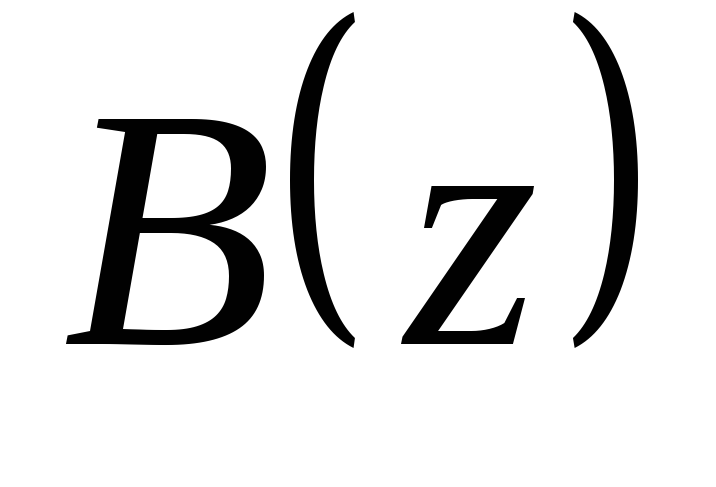 .
В этом случае при определении выражения
для решетчатой функции, описывающей
реакцию системы на единичное ступенчатое
воздействие, можно воспользоваться
формулой:
.
В этом случае при определении выражения
для решетчатой функции, описывающей
реакцию системы на единичное ступенчатое
воздействие, можно воспользоваться
формулой:
![]() , (64)
, (64)
где
![]() -порядок
характеристического уравнения замкнутой
системы;
-порядок
характеристического уравнения замкнутой
системы;![]() -
корень характеристического уравнения;
-
корень характеристического уравнения;![]() .
.
для рассматриваемой САУ дискретные значения выходного сигнала системы, наблюдаемые в моменты квантования, вычисляются по формуле:
![]() .
.
Значения решетчатой функции
![]() ,
вычисленные при
,
вычисленные при![]() и
и![]() ,
должны совпадать соответственно с
начальным и установившимся значениями
выходного сигнала системы, определенными
по формулам (62) и (63).
,
должны совпадать соответственно с
начальным и установившимся значениями
выходного сигнала системы, определенными
по формулам (62) и (63).
Для нахождения
![]() модифицированное
модифицированное![]() -
изображение выходного сигнала
представляется в виде суммы трех
слагаемых:
-
изображение выходного сигнала
представляется в виде суммы трех
слагаемых:
![]()
![]()
Каждому из них соответствует одно из
трех слагаемых в выражении
![]() .
Для определения первых двух может быть
использована формула (64).
При этом, вычисляя первое слагаемое
модифицированной решетчатой функции,
.
Для определения первых двух может быть
использована формула (64).
При этом, вычисляя первое слагаемое
модифицированной решетчатой функции,![]() следует считать равным
следует считать равным![]() ,
а при вычислении второго слагаемого
,
а при вычислении второго слагаемого![]() .
Третье слагаемое
.
Третье слагаемое![]() не
имеет нулевого корня, поэтому при
вычислении третьей составляющей
не
имеет нулевого корня, поэтому при
вычислении третьей составляющей![]() полагаем
полагаем![]() ,
но параметр
,
но параметр![]() в (64) заменяем на
в (64) заменяем на![]() .
При вычислении всех трех слагаемых в
выражении
.
При вычислении всех трех слагаемых в
выражении![]() считаем, что
считаем, что
![]() .
.
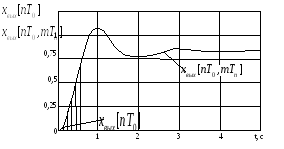
Рис. 55 Графики функций
![]() и
и![]()
нескорректированной дискретной САУ
Для произвольных моментов времени
![]() величина выходного сигнала рассматриваемой
системы равна:
величина выходного сигнала рассматриваемой
системы равна:
![]()
![]()
![]()
Здесь
![]() .
.
На рис. 55 приведены графики функций
![]() и
и![]() .
.
Построение логарифмических амплитудно- и фазочастотных характеристик (ЛАХ и ФЧХ) дискретных систем выполняется в функции абсолютной псевдо частоты
 ,
связанной с частотой
,
связанной с частотой следующей зависимостью:
следующей зависимостью:
![]()
Переход к частотным характеристикам
производится в два этапа. Первоначально
необходимо вычислить передаточную
функцию
![]() ,
для чего в передаточной функции
нескорректированной системы
,
для чего в передаточной функции
нескорректированной системы![]() переменная
переменная![]() полагается равной:
полагается равной:
![]()
Затем в полученном выражении
![]() делается
замена
делается
замена![]() .
.
Построение асимптотической ЛАХ
![]() по виду
по виду![]() производится по тем же правилам, что и
для непрерывных систем. При построении
ФЧХ
производится по тем же правилам, что и
для непрерывных систем. При построении
ФЧХ![]() следует обращать внимание на наличие
неминимально - фазового сомножителя
следует обращать внимание на наличие
неминимально - фазового сомножителя![]() в числители функции
в числители функции![]() .
Определяемая им составляющая
.
Определяемая им составляющая![]() равна:
равна:
![]()
Для рассматриваемой системы:
![]() ;
;
![]()
ЛАХ и ФЧХ нескорректированной разомкнутой системы приведены на рис. 56.
Один из возможных способов коррекции дискретных САУ основывается на использовании аналогового корректирующего звена, включенного последовательно в непрерывную часть системы, как показано на рис. 57. При этом передаточная функция разомкнутой скорректированной системы равна:
![]() (65)
(65)
90
20
0
0
-90
-20
-180
-40
-270
-60 1 400 20 2

























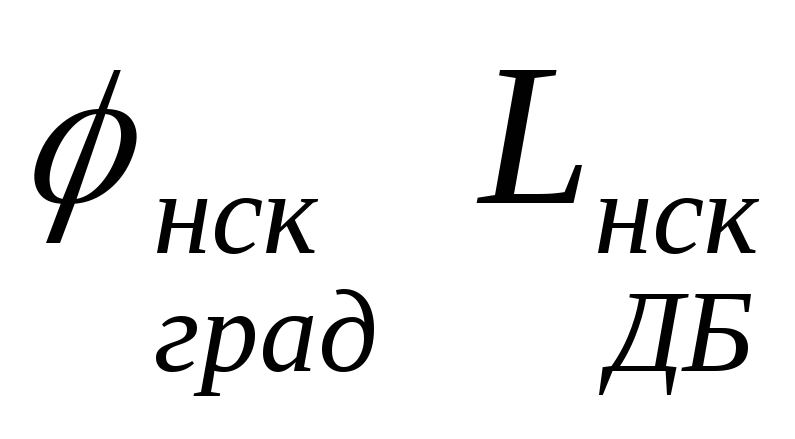
![]()
![]()

![]()
Рис. 56Логарифмические частотные характеристики
нескорректированной дискретной САУ
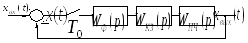
Рис. 57 Структурная схема дискретной САУ с последовательным
аналоговым корректирующим звеном
Для нахождения передаточной функции
![]() предварительно необходимо определить
желаемую передаточную функцию
предварительно необходимо определить
желаемую передаточную функцию![]() .
С этой целью сначала строится желаемая
ЛАХ разомкнутой скорректированной
системы
.
С этой целью сначала строится желаемая
ЛАХ разомкнутой скорректированной
системы![]() .
Построение
.
Построение![]() осуществляется по методикам, разработанным
для непрерывных САУ, с учетом всех
требований, предъявляемых к дискретной
системе. Для рассматриваемого примера
вид желаемых характеристик
осуществляется по методикам, разработанным
для непрерывных САУ, с учетом всех
требований, предъявляемых к дискретной
системе. Для рассматриваемого примера
вид желаемых характеристик![]() и
и![]() приведен на рис. 58. Частотная характеристика
дискретной САУ с фиксатором обязательно
имеет в числителе сомножитель
приведен на рис. 58. Частотная характеристика
дискретной САУ с фиксатором обязательно
имеет в числителе сомножитель![]() ,
поэтому выбранной желаемой ЛАХ
соответствуют следующие выражения для
,
поэтому выбранной желаемой ЛАХ
соответствуют следующие выражения для![]() и
и![]() :
:
![]() ,
,
![]()
