
- •Лекции по курсу
- •1. Общие сведения
- •1.1 Типы квантования непрерывных сигналов.
- •1.2. Решетчатые функции разностные уравнения.
- •1.3. Обобщенная структурная схема дискретной системы.
- •1.4. Простейший импульсный элемент. Формирующий элемент. Фиксатор.
- •2. Основы теории z-преобразования
- •2.1. Дискретное преобразование Лапласа. Z-преобразование.
- •2.2. Основные теоремы z-преобразования.
- •2.3. Передаточная функция разомкнутой дискретной системы.
- •2.4. Последовательное соединение звеньев в дискретных сау.
- •2.5. Передаточная функция замкнутой дискретной системы.
- •2.6. Обратное z-преобразование.
- •3. Анализ устойчивости и точности
- •3.1 Прямой метод оценки устойчивости.
- •3.2 Критерий устойчивости Шур-Кона.
- •3.3 Критерий устойчивости, использующий билинейное преобразование.
- •3.4. Абсолютно устойчивые системы.
- •3.5. Анализ точности дискретных систем.
- •4. Частотные характеристики дискретных систем
- •4.1. Теорема Котельникова-Шеннона.
- •4.2. Логарифмические частотные характеристики дискретных сау.
- •5. Определение реакции дискретной сау
- •5.1. Метод дробного квантования.
- •5.2. Метод модифицированного z-преобразования.
- •6. Системы автоматического управления
- •6.1. Структура системы.
- •6.2. Передаточные функции цву, реализующего типовые законы управления.
- •7. Коррекция цифровых систем управления
- •7.1. Коррекция дискретных сау с помощью непрерывных регуляторов.
- •7.2. Коррекция сау с помощью цифровых регуляторов.
- •7.3. Физическая реализуемость цифровых регуляторов.
- •7.4. Реализация цифровых регуляторов импульсными фильтрами.
- •7.5. Реализация цифровых регуляторов на базе цву.
- •8. Методические указания и вариаты расчетно-графического задания
- •90 20 0 0 -90 -20 -180 -40 -270 -60 20 2 1
6. Системы автоматического управления
С ЦИФРОВЫМ ВЫЧИСЛИТЕЛЬНЫМ УСТРОЙСТВОМ
В КОНТУРЕ РЕГУЛИРОВАНИЯ
6.1. Структура системы.
Передаточная функция цифрового вычислительного устройства.
Введение цифрового вычислительного устройства (ЦВУ) в контур регулирования может преследовать различные цели. Наиболее интересная среди них с точки зрения управления заключается в обеспечении требуемых динамических характеристик САУ. Эта цель достигается за счет использования соответствующей программы ЦВУ реализующей требуемый закон управления.
Структура управления САУ с цифровым вычислительным устройством в контуре управления приведена на рис. 34.
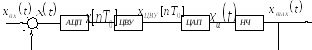
Рис. 34. Структура САУ с ЦВУ в контуре управления: АЦП – аналого-цифровой преобразователь;
ЦАП – цифро-аналоговый преобразователь; НЧ – непрерывная часть системы
ЦВУ в
контуре управления функционирует
следующим образом. С выхода АЦП на вход
ЦВУ с периодом
![]() поступает последовательность чисел
поступает последовательность чисел![]() (обычно в двоичном коде). С этим же
периодом ЦВУ формирует на выходе
последовательность
(обычно в двоичном коде). С этим же
периодом ЦВУ формирует на выходе
последовательность![]() ,
дискреты которой преобразуются ЦАП в
аналоговые сигналы определенного
уровня. В первом приближении можно
считать, что дискреты решетчатых функций
,
дискреты которой преобразуются ЦАП в
аналоговые сигналы определенного
уровня. В первом приближении можно
считать, что дискреты решетчатых функций![]() и
и![]() не сдвинуты друг относительно друга во
времени.. Это значит, что время расчета
ЦВУ очередного значения
не сдвинуты друг относительно друга во
времени.. Это значит, что время расчета
ЦВУ очередного значения![]() много меньше интервала квантования.
Для расчета
много меньше интервала квантования.
Для расчета![]() вn-м такте ЦВУ может
использовать:
вn-м такте ЦВУ может
использовать:
- все ранее
рассчитанные значения
![]() ,
гдеnизменяется от 0
до (n-1);
,
гдеnизменяется от 0
до (n-1);
- очередное
и прежние значения входного сигнала
![]() .
.
Но для
этого ЦВУ должно обладать неограниченной
памятью, в которой бы хранились эти
значения. Поэтому программа вычисления
![]() ,
которую реализует устройство,
предусматривает конечную глубину
памяти, напримерSпредшествующих значений выходного
сигнала ЦВУ иkзначений
входного сигнала. Тогда выражение для
,
которую реализует устройство,
предусматривает конечную глубину
памяти, напримерSпредшествующих значений выходного
сигнала ЦВУ иkзначений
входного сигнала. Тогда выражение для![]() может быть представлено в виде:
может быть представлено в виде:
![]()
Пусть s=k. Тогда выполнивZ-преобразование над обеими частями этого равенства, получим:
![]()
Введем в рассмотрение передаточную функцию ЦВУ:
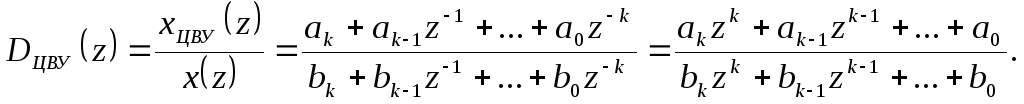
Необходимо учитывать то, что приведенная передаточная функция не отражает влияния таких факторов, как ограниченная разрядность, объем памяти и скорость расчета ЦВУ.
6.2. Передаточные функции цву, реализующего типовые законы управления.
Рассмотрим подробнее реализацию вычислительным устройством П-, ПИ- и ПИД- законов управления.
Очевидно,
что пропорциональное управление сводится
к простому умножению дискрет
![]() на некоторую константу
на некоторую константу![]() ,
т.е.
,
т.е.
![]() (46)
(46)
Численное
интегрирование может быть выполнено
различными способами. Это определяется
тем, какой из методов дискретизации
интеграла от функции
![]() реализует ЦВУ. В качестве приближенного
значения интеграла можно взять площадь,
ограниченную ступенчатой кривой,
проведенной через дискреты интегрируемой
функции (рис. 35). При этом алгоритм работы
на ЦВУ описывается разностным уравнением:
реализует ЦВУ. В качестве приближенного
значения интеграла можно взять площадь,
ограниченную ступенчатой кривой,
проведенной через дискреты интегрируемой
функции (рис. 35). При этом алгоритм работы
на ЦВУ описывается разностным уравнением:
![]()
Применив операцию Z-преобразования к этому уравнению, получим:
![]() ,
,
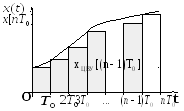
Рис. 35. К выполнению операции
численного интегрирования
откуда:
![]() (47)
(47)
Иную передаточную функцию цифрового интегратора получим, если интегрирование производится по несколько более точному методу трапеции (рис. 36), согласно которому:
![]()
Выполнив Z-преобразование, получим:
![]()
тогда
![]() (48)
(48)
Если более
точное интегрирование можно обеспечить,
применяя параболическую аппроксимацию
функции
![]() .
Тогда согласно формуле Симпсона
реализуется следующий алгоритм:
.
Тогда согласно формуле Симпсона
реализуется следующий алгоритм:
![]()
При этом передаточная функция интегратора:
![]() (49)
(49)
Необходимо
учитывать, что стремление к повышению
точности интегрирования за счет повышения
порядка
![]() может привести к усложнению аппаратной
реализации вычислительного устройства,
а также к увеличению интервала квантования,
что особенно критично для систем;
управление которыми осуществляется в
реальном масштабе времени.
может привести к усложнению аппаратной
реализации вычислительного устройства,
а также к увеличению интервала квантования,
что особенно критично для систем;
управление которыми осуществляется в
реальном масштабе времени.
В качестве
приближенного значения производной
функции
![]() можно использовать отношение первой
обратной разности решетчатой функции
можно использовать отношение первой
обратной разности решетчатой функции![]() к интервалу дискретности. В этом случае
уравнение ЦВУ имеет вид:
к интервалу дискретности. В этом случае
уравнение ЦВУ имеет вид:
![]()
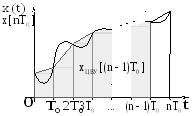
Рис. 36. К выполнению операции
численного интегрирования
методом трапеций
а передаточная функция цифрового дифференцирующего устройства:
![]() (50)
(50)
Используя (47)-(50), можно записать передаточные функции вычислительных устройств, реализующих более сложные законы управления. Так, передаточная функция ПИ-регулятора для случая, когда интегрирование производится по методу трапеции, равна:
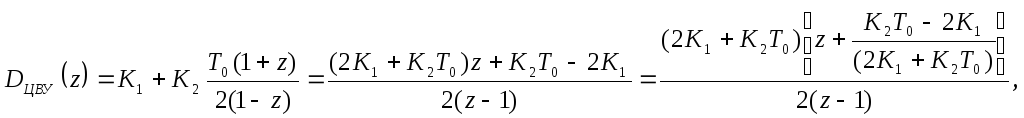 (51)
(51)
а передаточная функция ЦВУ, осуществляющего ПИД-закон регулирования, имеет следующий вид:
![]() (52)
(52)
