
- •Лекции по курсу
- •1. Общие сведения
- •1.1 Типы квантования непрерывных сигналов.
- •1.2. Решетчатые функции разностные уравнения.
- •1.3. Обобщенная структурная схема дискретной системы.
- •1.4. Простейший импульсный элемент. Формирующий элемент. Фиксатор.
- •2. Основы теории z-преобразования
- •2.1. Дискретное преобразование Лапласа. Z-преобразование.
- •2.2. Основные теоремы z-преобразования.
- •2.3. Передаточная функция разомкнутой дискретной системы.
- •2.4. Последовательное соединение звеньев в дискретных сау.
- •2.5. Передаточная функция замкнутой дискретной системы.
- •2.6. Обратное z-преобразование.
- •3. Анализ устойчивости и точности
- •3.1 Прямой метод оценки устойчивости.
- •3.2 Критерий устойчивости Шур-Кона.
- •3.3 Критерий устойчивости, использующий билинейное преобразование.
- •3.4. Абсолютно устойчивые системы.
- •3.5. Анализ точности дискретных систем.
- •4. Частотные характеристики дискретных систем
- •4.1. Теорема Котельникова-Шеннона.
- •4.2. Логарифмические частотные характеристики дискретных сау.
- •5. Определение реакции дискретной сау
- •5.1. Метод дробного квантования.
- •5.2. Метод модифицированного z-преобразования.
- •6. Системы автоматического управления
- •6.1. Структура системы.
- •6.2. Передаточные функции цву, реализующего типовые законы управления.
- •7. Коррекция цифровых систем управления
- •7.1. Коррекция дискретных сау с помощью непрерывных регуляторов.
- •7.2. Коррекция сау с помощью цифровых регуляторов.
- •7.3. Физическая реализуемость цифровых регуляторов.
- •7.4. Реализация цифровых регуляторов импульсными фильтрами.
- •7.5. Реализация цифровых регуляторов на базе цву.
- •8. Методические указания и вариаты расчетно-графического задания
- •90 20 0 0 -90 -20 -180 -40 -270 -60 20 2 1
5. Определение реакции дискретной сау
МЕЖДУ МОМЕНТАМИ КВАНТОВАНИЯ
Как уже
отмечалось, Z-преобразование
выходного сигнала дискретной системы
определяет значение функции![]() ,
только в моменты квантования
,
только в моменты квантования![]()
![]() .
Следовательно, методZ-преобразования
обладает достаточной точностью
применительно к тем системам, в которых
сигналы между двумя последовательными
моментами квантования изменяются не
существенно. Если же возникает
необходимость в определении реакции
системы между этими моментами, следует
использовать специальные методы,
например метод дробного квантования
или метод модифицированногоZ-преобразования.
.
Следовательно, методZ-преобразования
обладает достаточной точностью
применительно к тем системам, в которых
сигналы между двумя последовательными
моментами квантования изменяются не
существенно. Если же возникает
необходимость в определении реакции
системы между этими моментами, следует
использовать специальные методы,
например метод дробного квантования
или метод модифицированногоZ-преобразования.
5.1. Метод дробного квантования.
Как и
обычный метод Z-преобразования,
рассматриваемый метод не позволяет
найти непрерывный сигнал![]() ,
а лишь определить соответствующую ему
решетчатую функцию. Но дискреты этой
функции разделены интервалами времени,
равными
,
а лишь определить соответствующую ему
решетчатую функцию. Но дискреты этой
функции разделены интервалами времени,
равными![]() (гдеN– целое число),
т.е. расположены вNраз чаще по сравнению с дискретной
функцией
(гдеN– целое число),
т.е. расположены вNраз чаще по сравнению с дискретной
функцией![]() .
Обозначим такую решетчатую функцию
.
Обозначим такую решетчатую функцию![]() ,
а соответствующее ейZ-изображение
-
,
а соответствующее ейZ-изображение
-![]() .
Согласно методу дробного квантования
указанноеZ-изображение
равно
.
Согласно методу дробного квантования
указанноеZ-изображение
равно
![]() (41)
(41)
где
![]() может быть получена из обычной передаточной
функции системы
может быть получена из обычной передаточной
функции системы![]() заменой
в последнейzна
заменой
в последнейzна![]() ,
и
,
и![]() на
на![]() .
ВеличинаNопределяется
числом требуемых дополнительных значений
.
ВеличинаNопределяется
числом требуемых дополнительных значений![]() .
Если внутри интервала квантования
требуетсяRдополнительных
точек, то
.
Если внутри интервала квантования
требуетсяRдополнительных
точек, то![]() .
.
Пример 24. Воспользуемся исходными данными примера 17 и определим два дополнительных значения внутри интервала квантования для решетчатой переходной функции.
Поскольку
![]() ,
то
,
то![]() .
Передаточная функция дробного квантования,
полученная по
.
Передаточная функция дробного квантования,
полученная по![]() примера
17:
примера
17:
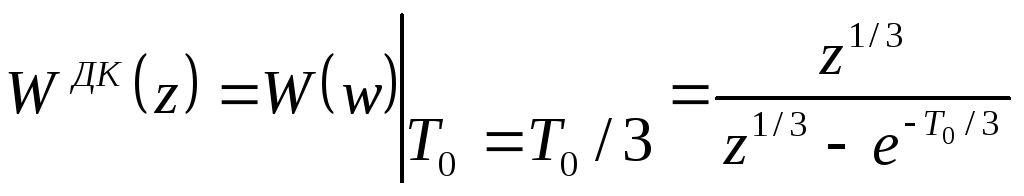
![]()
Z-изображение переходной функции в соответствии с (41):
![]()
Дробная
степень zв последнем
выражении затрудняет дальнейшие
преобразования, поэтому можно ввести
в рассмотрение новую переменную![]() ,
тогда:
,
тогда:
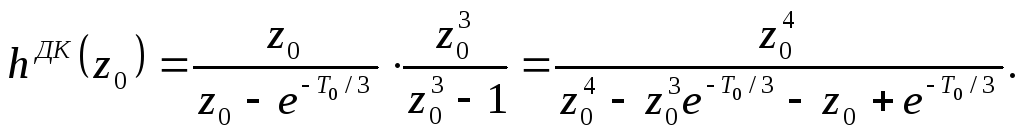
Разлагая
![]() в ряд Лорана, получим:
в ряд Лорана, получим:
![]()
Следовательно:
![]()
![]() и т.д.
и т.д.
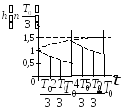
Рис.32. Переходная функция дискретной САУ (к примеру 24)
Очевидно,
что приведенный на рис. 22 возможный вид
графика функции
![]() ,
построенный по значениям дискрет функции
,
построенный по значениям дискрет функции![]() ,
неверен (рис. 32). В данном случае в этом
легко убедиться и без применения дробного
квантования, достаточно воспользоваться
формулой (10). Но при определении вида
непрерывных сигналов в более сложных
дискретных системах возможность
получения дополнительных дискрет внутри
интервала квантования является
несомненным достоинством рассмотренного
метода.
,
неверен (рис. 32). В данном случае в этом
легко убедиться и без применения дробного
квантования, достаточно воспользоваться
формулой (10). Но при определении вида
непрерывных сигналов в более сложных
дискретных системах возможность
получения дополнительных дискрет внутри
интервала квантования является
несомненным достоинством рассмотренного
метода.
5.2. Метод модифицированного z-преобразования.
Формально
этот метод основан на определении
Z-изображениямодифицированного
сигнала
![]() ,т.е. сигнала
,т.е. сигнала![]() ,
задержанного фиктивным звеном чистого
запаздывания на время
,
задержанного фиктивным звеном чистого
запаздывания на время![]() .
.
Рассмотрим
подробнее один, например первый, интервал
квантования (рис. 33). Поскольку
![]() ,
очевидно, что, изменяя
,
очевидно, что, изменяя![]() от 1 до 0, можно по величине дискреты
от 1 до 0, можно по величине дискреты
![]() определить все значения
определить все значения![]() от
от![]() до
до![]() .
Для удобства дальнейших преобразований
введем в рассмотрение величину
.
Для удобства дальнейших преобразований
введем в рассмотрение величину![]() ,
диапазон изменения которой от 0 до 1.
,
диапазон изменения которой от 0 до 1.
Z-изображение модифицированного сигнала:
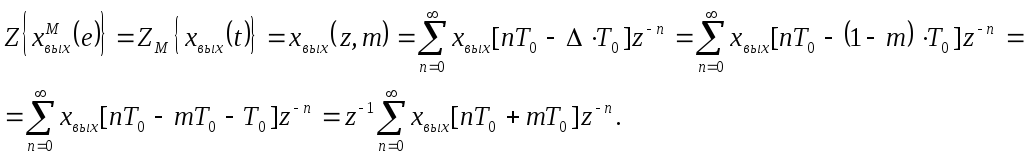
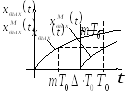
Рис.33. К определению метода модифицированного Z-преобразования
При
![]()
![]() и, следовательно, функция
и, следовательно, функция
![]() задержана на один такт по сравнению с
задержана на один такт по сравнению с![]() .
При
.
При![]()
![]() ,
т.е. модифицированное и “обычное”Z-изображения совпадают.
,
т.е. модифицированное и “обычное”Z-изображения совпадают.
Пример
25. Необходимо определить модифицированное
изображение линейно нарастающего
сигнала
![]() .
.
В соответствии с (42) получим:
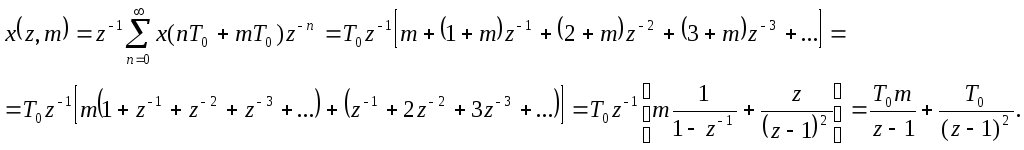
При
![]()
![]() .
.
Модифицированное Z-изображение
выходного сигнала разомкнутой системы
(см. рис. 13) с передаточной функцией ПНЧ![]() определим следующим образом:
определим следующим образом:
![]() (43)
(43)
где
![]() - модифицированная дискретная передаточная
функция, для вычисления которой необходимо
выполнить модифицированноеZ-преобразование
функции веса, соответствующей
- модифицированная дискретная передаточная
функция, для вычисления которой необходимо
выполнить модифицированноеZ-преобразование
функции веса, соответствующей![]() :
:
![]() (44)
(44)
При последовательном соединении звеньев дискретной САУ (см. рис. 14,а) модифицированное Z-изображение ее выходного сигнала равно:
![]()
а в случае,
когда звенья
![]() и
и![]() не разделены квантователем (см. рис.
14,б):
не разделены квантователем (см. рис.
14,б):
![]()
В замкнутой
дискретной системе с квантованием
сигнала ошибки (см. рис. 17) модифицированное
Z-изображение выходного
сигнала равно:![]() ,
но
,
но![]() следовательно:
следовательно:
![]()
и
![]()
а модифицированная дискретная передаточная функция замкнутой системы:
![]() (45)
(45)
Пример 26.
Необходимо определить решетчатые
переходные функции
![]() и
и![]() для дискретной системы, рассмотренной
в примере 22.
для дискретной системы, рассмотренной
в примере 22.
Имеем:
![]()
![]()
Для определения
![]() воспользуемся формулой (30). Полагаем:
воспользуемся формулой (30). Полагаем:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Тогда:
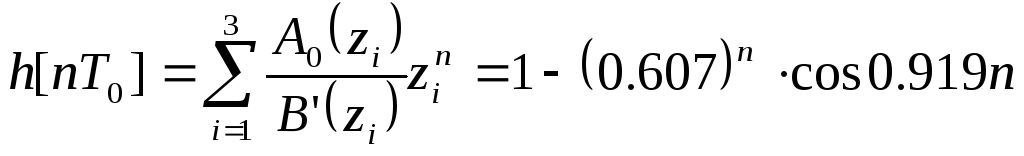
Величины
дискрет:
![]()
![]()
![]() и т.д.
и т.д.
Модифицированные дискретные передаточные функции разомкнутой и замкнутой систем равны соответственно:
![]()
![]()
и
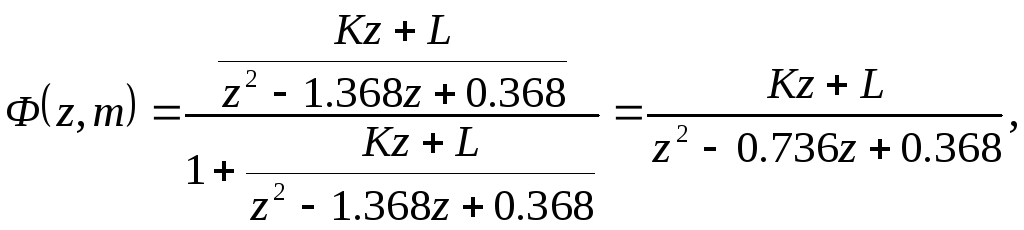
где
![]() ,
,![]()
Здесь важно
отметить тот факт, что для любой дискретной
системы характеристические полиномы
у
![]() и
и![]() совпадают, а следовательно, совпадают
и полюса указанных передаточных функций,
поэтому устойчивость САУ можно оценивать
как по
совпадают, а следовательно, совпадают
и полюса указанных передаточных функций,
поэтому устойчивость САУ можно оценивать
как по![]() ,
так и по
,
так и по![]() .
.
Более того,
выражение для
![]() может быть определено по
может быть определено по![]() :
:
![]()
Модифицированное Z-изображение переходной функции:
![]()
Раздельно
для каждого из двух слагаемых
![]() по формуле (30) необходимо определить
составляющие
по формуле (30) необходимо определить
составляющие![]() .
При этом полагаем
.
При этом полагаем![]() ,
так как они не зависят отn.
,
так как они не зависят отn.
После
преобразований получаем выражение для
![]() ,
по которому величину переходной функции
можно рассчитать для произвольных
моментов времени
,
по которому величину переходной функции
можно рассчитать для произвольных
моментов времени![]() .
.
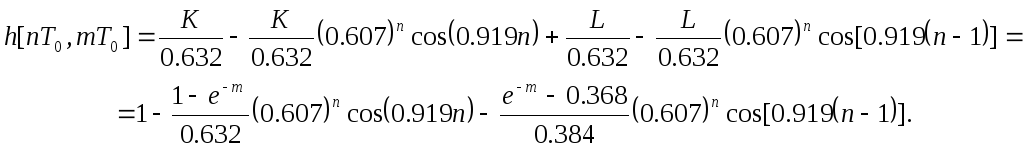
Например, при
![]() и
и![]() ;
при
;
при![]() и
и![]() .
.
