Задание:

1. Произвести расчет цепи по законам Кирхгофа и определить все токи.

2. Произвести расчет цепи и определить токи методом контурных токов.

3. Выполнить проверку расчета по балансу мощностей.

4. Произвести расчет цепи методом узловых потенциалов (Узел, потенциал которого принимается за 0, указан в карточке).

5. Рассчитать указанный в карточке ток методом наложения.

6. Рассчитать указанный в карточке ток методом эквивалентного генератора.

7. Смоделировать электрическую цепь по пункту 1, 4, 6.

Дано:

R₁=5 Ом Е₃=0.5 В

R₂=7 Ом E₇=0.5 В

R₄=2.8 Ом I_k=0.06 А

R₅=4.2 Ом

R₆=7 Ом

R₇=5 Ом

I₄=I₅=I₄₅,

I₃, I₄, I₅, I₆, I₇, I₁ -?

1. Расчёт цепи по законам Кирхгофа

1. Цепь содержит 6 ветвей с неизвестными токами ( m_t=6 ) и четыре узла ( n_y=4 ). Одна ветвь содержит источник тока I_k. Цепь питает 2 источника ЭДС E₃ и E₇. Выберем направления токов, как указано в карточке.

2. Определим достаточное количество уравнений для расчёта цепи по законам Кирхгофа.

По I закону Кирхгофа: N_I=n_y-1=3

По II закону Кирхгофа: N_II=m_в-(n_y-1)=3

3. Составим систему уравнений по I и II законам Кирхгофа (Полученную систему решаем в среде MathCad)

I закон Кирхгофа :

Узел 1: -I₇-I₂-I₄₅-I_k=0 -I₇-I₂-I₄₅=0,06

Узел 2: I₂-I₁-I₃=0 I₂-I₁-I₃=0

Узел 3: I₃+I_k+I₄₅-I₆=0 I₃+I₄₅-I₆=-0,06

II закон Кирхгофа 

I контур: -I₄₅(R₄+R₅)+I₂R₂=E₃ -7I₄₅+7I₂=0,5

II контур: I₇R₇-I₁R₁-I₂R₂=E₇ 5I₇-5I₁-7I₂=0,5

III контур: I₁R₁-I₆R₆=-E₃ 5I₁-7I₆=-0,5

4. Токи в ветвях:

I₁=-0,059

I₂=-0,008811

I₃=0.05

I₄₅=-0,08

I₆=0.03

I₇=0.029

2. Метод контурных токов

1. Цепь содержит 6 ветвей с неизвестными токами ( m_t=6 ) и четыре узла ( n_y=4 ). Одна ветвь содержит источник тока I_k. Цепь питает 2 источника ЭДС E₃ и E₇. Выберем направления токов, как указано в карточке.

2. Определим достаточной количество уравнений для расчёта цепи по методу контурных токов: N=m_в-(n_y-1)=3

3. Выделим в схеме три независимых контура, по которым замкнём токи I_{11 ,} I_{22 ,} I₃₃. Направление действия контурных токов выберем по часовой стрелке. Положительное направление обхода контура совместим с направлением контурного тока.

4. Система контурных уравнений имеет вид:

I₁₁(R₅+R₄+R₂) + I_kk(R₄+R₅) - I₂₂R₂=E₃

I₂₂(R₂+R₁+R₇) – I₁₁R₂ - I₃₃R₁=E₇

I₃₃(R₁+R₆)-I₂₂R₁=-E₃

5. Подставляя числовые значения, получаем (Решаем систему в среде MathCad):

14I₁₁+ 7I_kk- 7I₂₂=0,05

17I₂₂ - 7I₂₂ - 5I₃₃=0,05

12I₃₃-5I₂₂=-0,5

6. Контурные токи равны:

I₁₁=0,02

I₂₂=0,029

I₃₃=-0,03

7. Выполним расчёт действительных токов:

I₁=I₃₃-I₂₂=-0,059

I₂=I₁₁-I₂₂=-0,009

I₃=-I₃₃+I₁₁=0.05

I₄₅=-I₁₁-I_kk=-0,08

I₆=-I₃₃=0.03

I₇=I₂₂=0.029

3. Проверка расчёта по балансу мощностей

1. Правильность расчёта установим путём проверки баланса мощностей. Мощность, поступающая в цепь от источников энергии, должна равняться сумме мощностей потребителей электрической энергии: =

2. Предварительно найдём напряжение: U_k=I₄₅(R₄+R₅)

3. Полная мощность, развиваемая источниками энергии:

P_ист=-I_kU_k+E₇I₇+E₃I₃

4. P_потреб=I₁²R₁+I₂²R₂+I₄₅²(R₄+R₅)+I₆²R₆+I₇²R₇ =>

I₁²R₁+I₂²R₂+I₄₅²(R₄+R₅)+I₆²R₆+I₇²R₇= I₄₅(R₄+R₅)I_k+E₇I₇+E₃I₃

(-0,059)²*5+(-0,008811)²*7+(0,08)²*7+(0,03)²*7+(0,029)²*5=-(0,08)*7+0,5*0.029+0,5*0,05

0.0731≈0.0732 Вт

5. Погрешность расчета составляет δ%= 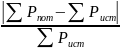·100%=0.136%