5. Анализ устойчивости двойственных оценок

Большой интерес представляет задача по определению интервалов изменения сырья, в которых оптимальный план двойственной задачи не меняется. Такое исследование называется анализом устойчивости двойственных оценок. Для этого используется следующая процедура.

Составляем матрицу А из элементов столбцов, соответствующих переменных х₃, х₄, х₅ таблицы 7, определяющей оптимальный план производства:

A=

Умножаем матрицу на вектор B= , где 400, 900, 600 - запасы сырья, соответственно, 1, 2, 3-го видов; rp_j (j = 1, 2, 3) – предполагаемое изменение соответствующего вида сырья.

A•B= =

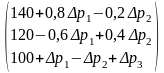
Записываем условие неотрицательности - компонент полученного вектора. (1.32)

Определим, при каких значениях rp₁, rp₂, rp₃ эта система неравенств верна. Очевидно, если rp₁ = rp₂ = 0, то rp₃ ≥ 100. Это означает, что если количество сырья 3-го вида будет уменьшено в пределах 100 кг или увеличено произвольным образом, то, несмотря на это, двойственные оценки сырья не изменятся.

Если rp₂ =rp₃ = 0, то решая систему (1.32), получим -100<rp₁ <200.

Если rp₁=rp₃ = 0, -300<rp₂ <100.

Это означает, что если количество одного из видов сырья 1-го или 2-го вида принадлежат соответственно промежуткам 300<rp₁ <600 или 600<rp₂ <1000, а количество остальных ресурсов остается первоначальным, то двойственные оценки сырья не меняются.

Если p₁, p₂ , p₃ изменяются одновременно, то для исследования влияния изменений на оптимальный план необходимо определить, принадлежат ли эти изменения rp₁, rp₂, rp₃ многоугольнику решений системы линейных неравенств (1.32). Точки этого многоугольника определяют количество сырья каждого вида, при котором двойственные оценки остаются прежними.

Предположим, что в рассматриваемой задаче изменения сырья составляют: rp₁ = 200 кг, rp₂ = 100 кг и rp₃ = 150 кг.

Определим, как при этом изменится оптимальный план, стоимость готовой продукции f и остатки сырья.

1-й способ. Подставим значения rp₁, rp₂, rp₃ в систему неравенств (1.32). Так как все неравенства остаются верными, это означает, что двойственные оценки сырья не изменятся. В этом случае изменение стоимости готовой продукции составит:

rf₁=y₁*rp₁+y₂*rp₂+y₃*rp₃ = 24*200+ 4*100+ 0*(-150) = 5200 (д.ед.),

т.е. стоимость готовой продукции по новому оптимальному плану равна

f₁=13200 + 5200 = 18400 (д.ед.).

Соответствующий план производства найдем следующим образом. Система ограничений, описывающая новые условия производства, примет вид: 2x₁+x₂ 600

3x₁+4x₂ 1000

X₁+3x₂ 450

X₁ 0, x₂ 0

Так как y₁>0 и y₂>0, то сырье 1-го и 2-го вида используется полностью. Поэтому 1-ое и 2-ое условия выполняются как равенство. Решая совместно систему 2x₁ + x₂ = 600

3x₁ + 4x₂= 1000,

получим новый оптимальный план производства x₁ = 280 ед.; x₂ = 40 ед. При этом остатки сырья составят: x₃ = x₄ = 0, x₅ = 50 кг.

2-й способ.

Умножим матрицу А на вектор В= = . В соответствии с таблицей 7 получим вектор базисных решений: =AB=

Т. к. базисные решения допустимы (неотрицательны), то решение двойственной задачи не изменилось. Оптимальное значение f найдем, умножая строку теневых цен С = (24; 4; 0) на вектор В (напомним, что теневые цены – это решение двойственной задачи, которое находится под матрицей А в нижней строке таблицы 7).

f = CB = 24·600 + 4·1000 + 0·450 = 18400 (д.ед.).

Если при изменении объемов сырья меняются двойственные оценки, т.е. при подстановке rp₁, rp₂, rp₃ в систему (1.32) неравенства становятся неверными, то формулируется новая производственная задача, которая может быть решена описанным выше симплексным методом.