1.1 Метод потенциалов.

Рассмотрим случай закрытой ТЗ.

Пусть x_ij - неизвестное количество единиц перевозимого груза по данному маршруту между пунктом i поставки и пунктом j потребления. Математически задача формулируется как каноническая задача линейного программирования: найти неотрицательное решение системы m + n линейных уравнений – ограничений вида:

п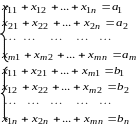 ри минимуме затрат на перевозки:

Z = c₁₁x₁₁ + c₁₂x₁₂ + ...+ c_mnx_{mn ,}

или в компактном виде:

(1.1)

a min (1.2)

В системе (1.1) первые m уравнений выражают условия баланса по строкам таблицы 1.1, остальные n уравнений - условия баланса по столбцам. Заметим, что не все уравнения системы (1.1) линейно независимы, сумма первых m уравнений совпадает с суммой остальных n уравнений. Легко показать, что количество независимых уравнений системы будет (m + n – 1), и одно (любое) уравнение можно отбросить. Поэтому базисных переменных будет столько же: (m + n – 1). Базисным переменным соответствуют заполненные клетки таблицы, а свободным переменным – пустые клетки.

Транспортная задача может быть решена обычным симплексным методом. Однако более эффективны методы, учитывающие следующие особенности данной задачи:

• ограничения задаются в виде уравнений;

• коэффициенты при неизвестных равны 1;

• каждое неизвестное входит лишь в два уравнения, причём один раз в условия баланса по строкам (первые m уравнений) и один раз в условия баланса по столбцам (остальные n уравнений).

Все способы решения, относящиеся к закрытой модели нетрудно обобщить также на случай открытой модели. Для этого достаточно дополнительно ввести в условия задачи фиктивного потребителя (остатки у поставщиков при ) или фиктивного поставщика (недопоставки потребителям при ), превратив открытую модель в закрытую. А чтобы функция затрат при этом не изменилась, установить тарифы перевозок к фиктивным потребителям или от фиктивных поставщиков равными нулю. Очевидно, минимум расходов новой закрытой модели будет совпадать с минимумом расходов исходной открытой модели, и, решив первую задачу, мы тем самым получим также и решение второй.

Проиллюстрируем основные этапы решения закрытой транспортной задачи на конкретном примере.

На три базы поступил однородный груз в количествах: а₁ = 120т на базу А₁, а₂ = 160т на базу А₂, а₃ = 120т на базу А₃. Полученный груз следует перевезти в четыре пункта, потребности которых составляют: b₁ = 40т в пункте В₁, b₂ = 80т в пункте В₂, b₃ = 80т в пункте В₃, b₄ = 200т в пункте В_4. Известны тарифы с_ij перевозок от i-го (i = 1, 2, 3) поставщика к j-му (j = 1, 2, 3, 4 ) потребителю. Условия задачи представим таблицей 1.2 (с_ij записаны в верхнем правом углу каждой клетки таблицы).

Необходимо закрепить поставщиков за потребителями так, чтобы общая сумма затрат на перевозку была минимальной.

Решение транспортной задачи начинается с отыскания первого опорного плана. Существует несколько схем построения первоначального плана: метод северо-западного угла, метод наименьшей стоимости, метод двойного предпочтения и другие. Однако в любом случае план должен иметь ровно (m + n – 1) заполненных клеток, а остальные (m – 1)( n – 1) клетки – пустые. Подчеркнём, пустая клетка и клетка, заполненная нулём, - не одно и то же.

Т аблица 1.2

Потребители Поставщики					Запасы
А1	4	4	6	6	120 = а1
А2	10	2	14	4	160 = а2
А3	14	6	8	12	120 = а3
П отребности	40 = b1	80 = b2	80 = b3	200 = b4	400 400

П остроим опорный плана по методу наименьшей стоимости. То есть в первую очередь будем удовлетворять тех потребителей, доставка товара к которым обходится дешевле, иными словами будем заполнять клетки с наименьшим тарифом. Выбираем в таблице 1.2 клетку А₂В₂ (краткое обозначение: (2, 2)), соответствующую наименьшему тарифу с₂₂ = 2. На базе A₂ имеется груз a₂ = 160 т. Потребность пункта В₂ составляет b₂ = 80т и может быть удовлетворена базой A₂. Полагая x₂₂ = 80, вписываем это значение в клетку (2, 2) и исключаем из рассмотрения второй столбец. На базе А₂ остаётся (160 – 80) = 80т. Остальная часть табл. 1.2 примет вид табл. 1.2.1.

Теперь наименьший тариф 4 - в двух клетках: (1, 1) и (2, 4). Выбираем клетку (2, 4), так как при этом будет перевезено 80т – больше, чем при выборе клетки (1, 1). Запасы А₂: 80т меньше потребностей В₄: 200т. Поэтому в клетку (2, 4) записываем число 80, исчерпав запасы А₂, а потребности В₄ уменьшаем на 80т.

Строку А₂ исключаем из рассмотрения и переходим к таблице 1.2.2. Теперь наименьшая стоимость: с₁₁ = 4. Закрываем потребности В₁, уменьшая запасы А₁ до 80т, в клетку (1, 1) ставим 40т и исключаем столбец В₁.

В новой таблице 1.2.3 наименьшая стоимость, равная 6, находится в клетках (1, 3) и (1, 4). Можно выбрать любую из них, поскольку объем перевозок для этих клеток одинаков. Пусть это будет клетка (1, 3). Запасы А₁ составляют 80т и совпадают с потребностями В₃. В клетку (1, 3) записываем число 80 и исключаем из рассмотрения либо строку А₁ либо столбец В₃. Если исключить и строку, и столбец, то число заполненных клеток будет меньше, чем m + n - 1 = 6, что недопустимо. Исключим столбец В₃. Получим таблицу 1.2.4, в которой остался только один ряд – столбец В₄, заполняемый однозначно: в клетку (1, 4) записываем 0 (вырожденный случай), в клетку (3, 4) - число 120. В результате (см. таблицу 1.2.5) заполненными оказываются следующие клетки матрицы перевозок X = :

x₁₁ = 40, x₁₃ = 80, x₁₄ = 0, x₂₂ = 80, x₂₄ = 80, x₃₄ = 120,.

Транспортные расходы по этой программе равны: Z = 40 4 + 80 6 + 0 6 + 80 2 + 80 4 + 120 12 = 2560 (д. ед.).

Таблица 1.2.5

Потребители Поставщики					Запасы
А1	4 40	4	6 80	6 0	120 = а1
А2	10	2 80	14	4 80	160 = а2
А3	14	6	8	12 120	120 = а3
Потребности	40 = b1	80 = b2	80 = b3	200 = b4	400 400

Напомним, что клетки таблицы, отвечающие базисным неизвестным матрицы перевозок, называют базисными или занятыми, а клетки, отвечающие свободным неизвестным, называются свободными или пустыми:

x₁₁, x₁₃, x₁₄, x₂₂, x₂₄, x₃₄ – базисные;

x₁₂, x₂₁, x₂₃, x₃₁, x₃₂, x₃₃ – свободные.

Отыскание первого опорного плана - это лишь подготовительный этап к решению задачи (нахождению оптимального плана). Число заполненных клеток, как было отмечено выше, должно быть равно (m + n – 1). В рассматриваемом примере это 6. После того, как первый базисный (опорный) план найден, следует проверить, является ли он оптимальным. Для этого можно воспользоваться методом потенциалов, основанным на следующей теореме.

Если план x^* = (x_ij^*) ( i = 1, …,m; j = 1, …,n ) транспортной задачи является оптимальным, то ему соответствуют m + n чисел u_i^* и v_j^*, удовлетворяющих условиям

u_i^* + v_j^* = с_ij, для x_ij ³ 0 (базисные клетки), (1.3)

u_i^* + v_j^* с_ij, для x_ij = 0 (свободные клетки), (1.4)

где u_i^* и v_j^* называются потенциалами соответственно строк (поставщиков) и столбцов (потребителей); с_ij - тарифы.

Для доказательства достаточно заметить, что потенциалы – это двойственные переменные (u, v) произвольного знака, соответствующие условиям баланса по строкам (u) и столбцам (v). Наоборот, каждой неотрицательной переменной x_ij исходной ТЗ соответствует дуальная переменная y_ij , а также ограничение - неравенство типа (1.4) двойственной задачи. При этом для базисных неизвестных неравенства превращаются в равенства (1.3) по принципу дополнительности (дополняющей нежёсткости).

Напомним, что дополнительные двойственные переменные y_ij (оценки клеток) равны разностям между правой и левой частями неравенств (1.4) (или равенств (1.3)). Нетрудно показать, что оценки клеток не изменятся, если все тарифы какого-либо ряда изменить на одну и ту же величину, причём эту операцию можно проделывать произвольное количество раз.

Таким образом, чтобы проверить план на оптимальность, следует найти потенциалы (таблица 1.3):

Таблица 1. 3

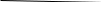Потребители Поставщики	v1 = 4	v2 = 4	v3 = 6	v4 = 6
u1 = 0 А1	4 40	4	6 80	6 0
u2 = -2 А2	10	2 80	14	4 80
u3 = 6 А3	14	6	8	12 120

Для нахождения потенциалов используем условие (1.3) для занятых клеток:

(1.5)

Система (1.5) состоит из шести независимых уравнений и имеет семь неизвестных. Так как независимых условий баланса: m + n - 1 = 6, то одно из неизвестных – лишнее, и его можно зафиксировать, например, приравняв к нулю. Пусть это будет u₁ = 0. Тогда остальные неизвестные последовательно найдутся из системы (1.5) единственным образом. Из первых трёх уравнений: v₁ = 4, v₃ = 6, v₄ = 6. Подставляя эти значения в последние два уравнения, найдем: u₂ = -2, u₃ = 6. Наконец из четвёртого уравнения: v₂ = 4.

После того, как потенциалы найдены (смотри таблицу 1.3), следует проверить условие оптимальности (1.4) для свободных клеток, то есть найти косвенные тарифы c^/_ij = u_i + v_j и сравнить их с истинными цифрами с_ij. Разность y_ij = c_ij – c^/_ij есть оценка пустой клетки, по второй теореме двойственности она равна коэффициенту при переменной x_ij в выражении функции затрат через свободные переменные.

Видим, что условие оптимальности (1.4) в свободных клетках ( 3, 2), ( 3, 3) нарушено, для них косвенные тарифы больше истинных, а оценки y₃₂ и y₃₃ – отрицательны. План перевозок может быть улучшен перераспределением поставок в пустую клетку с отрицательной оценкой. Если таких клеток несколько, то обычно выбирают клетку с максимальной по абсолютной величине отрицательной оценкой.

Для сохранения баланса в строках и столбцах поставки перераспределяют по определённому циклу.

Ц иклом в транспортной таблице называется обобщённый прямоугольник, одна вершина которого совпадает со свободной клеткой (для которой образуется цикл), а остальные вершины - с заполненными клетками, причём все стороны прямоугольника проходят строго вдоль строк и столбцов таблицы, и все его углы - прямые. Если вершины цикла, начиная с пустой клетки, пометить чередующимися знаками + - + - ¼, то получится цикл пересчета. Циклы могут иметь различную конфигурацию. Примеры возможных циклов приведены на рис. 1.1. Можно показать, что для любой пустой клетки цикл существует и он единственный!

Пересчет по циклу (сдвиг из отрицательных вершин в положительные) производят следующим образом:

• находят D - минимальную из поставок в отрицательных вершинах цикла;

• к поставкам в положительных вершинах прибавляют D, из поставок в отрицательных вершинах вычитают D;

• одну отрицательную клетку - вершину с уменьшенной до нуля поставкой - переводят в свободные.

В результате получится новый план перевозок, в котором одна свободная переменная заменяется на базисную, но при этом освобождается одна из базисных переменных. Равновесие между запасами и заявками не меняется, по-прежнему сумма перевозок в каждой i-той строке равна запасам а_i, а сумма перевозок в каждом j-ом столбце - заявке b_j.

Продолжим рассмотрение примера. Оценки y₃₂ = y₃₃ = - 4 одинаковы и отрицательны. Выберем, например, клетку (3, 2) и построим для неё цикл пересчёта:

(3, 2) – (3, 4) + (2, 4) – (2, 2).

Таблица 1.4

Потребители Поставщики	v1 = 4	v2 = 0	v3 = 6	v4 = 6
u1 = 0 А1	4 40	4	6 80	6 0
u2 = -2 А2	10	2	14	4 160
u3 = 6 А3	14	6 80	8	12 40

Среди отрицательных вершин цикла (2, 2) и (3, 4) находим клетку с наименьшей поставкой:

D = min { х_22; х₃₄} = min{80; 120} = 80.

Эта клетка (2, 2) становится свободной.

Производим сдвиг на найденное значение D = 80: х₃₄ и х₂₂ уменьшим на 80, а х₃₂ и х₂₄ увеличим на 80. Указанный сдвиг приведет к новому базисному решению (таблица 1.4)

Проверим, является ли новый план оптимальным. Значения потенциалов (см. таблицу 1.4) найдем из решения системы уравнений:

u₁+v₁=4

u₁+v₃=6

u₁+v₄=6

u₂+v₄=4

u₃+v₂=6

u₃+v₄=12

Пусть u₁=0, тогда v₁=4; v₃=6; v₄=6.

Зная v_4, найдем u₂=-2 и u₃=6, а зная u_3, найдем v₂=0.

Оценки пустых клеток: y₁₂ = 4 – u₁ – v₂ = 4; y₂₁ = 10 – u₂ – v₁ = 8;

y₂₂ = 2 – u₂ – v₂ = 4; y₂₃ = 14 – u₂ – v₃ = 10; y₃₁ = 14 – u₃ – v₁ = 4; y₃₃ = 8 – u₃ – v₃ = - 4.

План не оптимален, т.к. y₃₃ < 0. Построим цикл для клетки (3, 3):

(3, 3) – (3, 4) + (1, 4) – (1, 3).

“Отрицательным” клеткам цикла -(3, 4) и -(1, 3) соответствуют поставки х₃₄ = 40, х₁₃ = 80. D = min {40, 80} = 40. К поставкам х₃₃ и х₁₄ прибавляем D = 40, а из поставок х₃₄ и х₁₃ – вычитаем D, в результате клетка (3, 4) становится пустой, а клетка (3, 3) – заполненной (базисной). Новый план представлен в таблице 1.5:

Таблица 1. 5

Потребители Поставщики	v1 = 4	v2 = 4	v3 = 6	v4 = 6
u1 = 0 А1	4 40	4	6 40	6 40
u2 = -2 А2	10	2	14	4 160
u3 = 2 А3	14	6 80	8 40	12

Найдем потенциалы непосредственно по таблице 1.5, не выписывая явно систему уравнений. Сначала положим u₁ = 0; затем напротив заполненных клеток первой строки запишем: v₁ = 4 - u₁ = 4, v₃ = 6 - u₁ = 6, v₄ = 6 - u₁ = 6. Теперь напротив заполненных клеток третьего (v₃ - уже найдено!) и четвёртого (v₄ - также найдено!) столбцов: u₃ = 8 - v₃ = 2, u₂ = 4 - v₄ = - 2; наконец напротив заполненных клеток третьей строки: v₂ = 6 - u₃ = 4.

Оценки пустых клеток:

y₁₂ = 4 - (0 + 4) = 0; y₂₁ = 10- (-2 + 4) = 8; y₂₂ = 2 – (-2 + 4) = 0;

y₂₃ = 14 – (-2 + 6) = 10; y₃₁ = 14 – (2 + 4) = 8; y₃₄ = 12 – (2 + 6) = 4.

Все оценки неотрицательны, поэтому план X₁ таблицы 1.5 – оптимален!

. (1, 6)

Минимальные затраты:

Z = 40 4 + 40 6 + 40 6 + 160 4 + 80 6 + 40 8 = 2080 (д. ед.).

Заметим, что две оценки пустых клеток y₁₂ и y₂₂ – нулевые, значит по следствию №2 из второй теоремы двойственности найденный оптимальный план X₁ – не единственный. Ещё два базисных оптимальных плана X₂ и X₃, легко получаются из плана таблицы 1.5 сдвигом по циклам для вырожденных клеток (1, 2) и (2, 2):

(1, 2) – (1, 3) + (3, 3) – (3, 2); 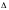= min { х_13; х₃₂} = 40;

; (1, 7)

(2, 2) – (2, 4) + (1, 4) – (1, 3) + (3, 3) – (3, 2); = min {х_24; х_13; х₃₂} = 40;

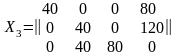. (1, 8)

Очевидно, оценки пустых клеток не изменяются. Каждый из новых планов имеет по две вырожденных клетки. Сдвиг по циклам для этих клеток в данной задаче не приводит к новым планам (проверьте!).

Любой оптимальный план перевозок X есть выпуклая линейная комбинация базисных планов: X = q₁X₁ + q₂X₂ + q₃X₃, где q₁ + q₂ + q₃ = 1; q_i ³ 0; i =1, 2, 3. Например, для q₁ = 0,5; q₂ = 0,25; q₃ = 0,25; оптимальный (но не базисный!) план примет вид:

.
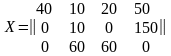