Введение		3
Общая постановка задачи линейного программирования (ЛП).		3
Геометрический метод решения задачи линейного программирования.		10
3. Симплексный метод решения задачи линейного программирования.		14
М-метод искусственного базиса.		18
Двойственные задачи линейного программирования и их использование.		20
Анализ устойчивости двойственных оценок.		24
Решение задачи линейного программирования с помощью Excel.		26
Тестовые вопросы.		32
Задачи контрольных заданий.		45
Рекомендуемая литература (основная и дополнительная).		47

Введение

Решение многовариантных задач в экономике является предметом курса исследования операций. Основной проблемой многовариантных задач является нахождение оптимального (наилучшего) решения. Наиболее распространены в экономике модели, которые представляют собой систему ограничений вкупе с критерием оптимальности.

В предлагаемой работе будут рассмотрены только такие модели, в которых система ограничений и критерий оптимальности являются линейными функциями искомых параметров.

1. Общая постановка задачи линейного программирования (лп)

Математическое программирование – это совокупность методов отыскания наибольшего (наименьшего) значения функции f при ограничениях, заданных m неравенствами:

f = f(x₁, …, x_n) Ì max (min); g_i(x₁, …, x_n) ≥ 0, i = 1, …, m. (1.1)

Функцию f называют функцией цели, или критерием оптимальности. Задача (1.1) сводится к задаче ЛП, если f и все g_i(i = 1, …, m) - линейные функции неотрицательных аргументов x_j, j = 1, …, n.

ЛП является наиболее разработанным разделом математического программирования, как вполне оформившаяся дисциплина прикладной математики. В терминах ЛП формулируется большое количество народнохозяйственных, технических, военных и других задач управления и планирования. Приведем примеры задач линейного программирования.

Задача о планировании производства.

Предприятие производит изделия трех видов v₁, v₂, v₃. По каждому виду изделий известен объем продаж, в соответствии с которым необходимо выпустить не менее b₁ единиц изделия v₁, не менее b₂ единиц изделия v₂ и не менее b₃ единиц изделия v₃. При этом план выпуска может быть перевыполнен, но в определенных границах; условия спроса ограничивают количества произведенных единиц изделия каждого вида: не более, соответственно, β_1, β_2, β₃ единиц.

На изготовление изделий используется четыре вида сырья: S₁, S₂, S₃, S₄, причем их запасы ограничены числами y₁, y₂, y₃, y₄ единиц каждого вида сырья. На изготовление каждого вида изделий идет определенное количество сырья каждого вида – a_ij (точнее, a_ij – количество единиц сырья вида S_i, потребляемое на изготовление одной единицы изделия v_j), см. табл. 1.

Таблица 1

Сырьё	Изделия
	v1	v2	v3
S1	a11	a21	a31
S2	a12	a22	a32
S3	a13	a23	a33
S4	a14	a24	a34

Реализация одного изделия v₁ приносит предприятию прибыль C₁, соответственно, v₂ - прибыль C₂, v₃ - прибыль C₃. Требуется так спланировать производство (сколько каких изделий производить), чтобы план был выполнен или перевыполнен (но при отсутствии «затоваривания»), а суммарная прибыль обращалась в максимум.

Запишем данную задачу в форме задачи линейного программирования. Элементами решения будут x₁, x₂, x₃ - количества единиц изделий v₁, v₂, v₃, которые необходимо произвести. Обязательность выполнения планового задания запишется в виде трех ограничений – неравенств:

x₁ ≥ b₁, x₂ ≥ b₂, x₃ ≥ b₃. (1.2)

Отсутствие излишней продукции (затоваривания) даст еще три ограничения – неравенства:

x₁ ≤ β ₁, x₂ ≤ β ₂, x₃ ≤ β₃. (1.3)

Каждого из четырех видов сырья должно хватить, отсюда следуют четыре ограничения – неравенства:

a₁₁x₁ + a₂₁x₂ + a₃₁x₃ ≤ y₁

a₁₂x₁ + a₂₂x₂ + a₃₂x₃ ≤ y₂

a₁₃x₁ + a₂₃x₂ + a₃₃x₃ ≤ y₃

a₁₄x₁ + a₂₄x₂ + a₃₄x₃ ≤ y₄ (1.4)

Прибыль, приносимая планом (x₁, x₂, x₃), будет равна:

L = C₁x₁ + C₂x₂ + C₃x₃. (1.5)

Таким образом, сформулирована задача линейного программирования: найти (подобрать) такие неотрицательные значения переменных x₁, x₂, x₃, чтобы они удовлетворяли неравенствам-ограничениям (1.2), (1.3), (1.4) и, вместе с тем, обращали в максимум линейную функцию этих переменных:

L = C₁x₁ + C₂x₂ + C₃x₃ Ì max. (1.6)

Задача о загрузке оборудования.

Малое предприятие располагает двумя видами универсальных станков N₁ и N₂. Каждый из станков может производить три вида изделий: Т₁, Т₂, Т₃, но с разной производительностью. Данные a_ij производительности станков даны в таблице 2 (первый индекс – тип станка, второй – вид изделия).

Таблица 2

Тип станка	Вид изделия
	Т1	Т2	Т3
1	a11	а12	а13
2	a21	а22	а23

Каждое изделие вида Т₁ приносит предприятию доход С₁, вида Т₂ - доход С₂, вида Т₃ - доход С₃. Предприятие, исходя их намеченного объема продаж, должно производить в месяц не менее b₁ изделий вида Т₁, b₂ изделий вида Т₂ и b₃ изделий вида Т₃. Количество изделий каждого вида не должно превышать, соответственно, β_1, β_2, β₃ штук.

Кроме того, все станки должны быть загружены. Требуется так распределить загрузку станков производством изделий Т₁, Т₂, и Т₃, чтобы суммарный месячный доход был максимален.

В этой задаче элементами решения являются количество станков, занятых производством изделий каждого вида. Всего будет шесть элементов решения, обозначим их через x с двумя индексами (первый – тип станка, второй – вид изделия):

x₁₁ x₁₂ x₁₃

x₂₁ x₂₂ x₂₃ (1.7)

Запишем условия-ограничения, наложенные на элементы решения x_ij. Прежде всего, необходимо обеспечить выполнение заданного объема продаж, что даст нам три неравенства-ограничения:

a₁₁x₁₁ + a₂₁x₂₁ ≥ b₁

a₁₂x₁₂ + a₂₂x₂₂ ≥ b₂

a₁₃x₁₃ + a₂₃x₂₃ ≥ b₃ (1.8)

После этого ограничим перевыполнение объема продаж, это даст нам еще три неравенства-ограничения:

a₁₁x₁₁ + a₂₁x₂₁ ≤ β₁

a₁₂x₁₂ + a₂₂x₂₂ ≤ β₂

a₁₃x₁₃ + a₂₃x₂₃ ≤ β₃ (1.9)

Теперь запишем ограничения, связанные с наличием оборудования и его полной загрузкой:

x₁₁ + x₁₂ + x₁₃ = N₁

x₂₁ + x₂₂ + x₂₃ = N₂ (1.10)

После чего запишем суммарный доход от производства всех видов изделий. Суммарное количество штук изделий Т₁, произведенное двумя станками, будет равно a₁₁x₁₁ + a₂₁x₂₁ и принесет доход C₁ (a₁₁x₁₁ + a₂₁x₂₁). Рассуждая аналогично, найдем суммарный доход предприятия за месяц при заданном объеме продаж (1.7):

L = C₁ (a₁₁x₁₁ + a₂₁x₂₁) + C₂ (a₁₂x₁₂ + a₂₂x₂₂) + C₃ (a₁₃x₁₃ + a₂₃x₂₃)

или, используя знаки суммирования, в более короткой записи:

(1.11)

Эту линейную функцию (1.11) шести аргументов необходимо обратить в максимум: L Ì max

Перед нами – опять задача линейного программирования: найти такие неотрицательные значения переменных x₁₁, x₁₂ … , x₂₃, которые, во-первых, удовлетворяли бы ограничениям-неравенствам (1.8), (1.9), во-вторых, - ограничениям-равенствам (1.10) и, наконец, обращали бы в максимум линейную функцию этих переменных (1.11).

Задача о снабжении сырьем.

Имеются три промышленных предприятия: П₁, П₂, П₃, требующих снабжения определенным видом сырья. Потребности в сырье каждого предприятия равны, соответственно, а₁, а₂, а₃ единиц. Имеются пять сырьевых баз, расположенных от предприятий на каких-то расстояниях и связанных с ними путями сообщения с разными тарифами. Единица сырья, полученная предприятием П_j с базы В_j, обходится предприятию в С_ij рублей (первый индекс – номер предприятия, второй – номер базы, см. таблицу 3).

Таблица 3.

Предприятие	База
	В1	В2	В3	В4	В5
П1	С11	С12	С13	С14	С15
П2	С21	С22	С23	С24	С25
П3	С31	С32	С33	С34	С35

Возможности снабжения сырьем с каждой базы ограничены их производственными мощностями, соответственно: b₁, b₂, b₃, b₄, b₅ единиц сырья. Требуется составить такой план снабжения предприятий сырьем, чтобы потребности предприятий были обеспечены при минимальных расходах на сырье.

Для этого поставим задачу линейного программирования, обозначив через x_ij количество сырья, получаемое i-м предприятием с j-базы. Всего план будет состоять из 15 элементов решения:

x₁₁ x₁₂ x₁₃ x₁₄ x₁₅

x₂₁ x₂₂ x₂₃ x₂₄ x₂₅

x₃₁ x₃₂ x₃₃ x₃₄ x₃₅ (1.12)

Введем ограничения по потребностям, т.е. каждое предприятие получит ровно столько сырья, сколько ему требуется:

x₁₁ + x₁₂ + x₁₃ + x₁₄ + x₁₅ = а₁

x₂₁ + x₂₂ + x₂₃ + x₂₄ + x₂₅ = а₂

x₃₁ + x₃₂ + x₃₃ + x₃₄ + x₃₅ = а₃ (1.13)

Далее запишем ограничения-неравенства, вытекающие из производственных мощностей баз:

x₁₁ + x₂₁ + x₃₁ ≤ b₁

x₁₂ + x₂₂ + x₃₂ ≤ b₂

x₁₃ + x₂₃ + x₃₃ ≤ b₃

x₁₄ + x₂₄ + x₃₄ ≤ b₄

x₁₅ + x₂₅ + x₃₅ ≤ b₅ (1.14)

Наконец, запишем, с учетом данных таблицы 3, суммарные расходы на сырье, которые необходимо минимизировать:

(1.15)

Таким образом, перед нами задача линейного программирования: необходимо найти такие неотрицательные значения переменных x_ij, которые удовлетворяли бы ограничениям-равенствам (1.13), ограничениям-неравенствам (1.14) и обращали бы в минимум их линейную функцию (1.15).

Задача о кормовом рационе.

В задаче о кормовом рационе x_j означает искомое количество кормов; а_ij – содержание питательного вещества i в корме j; b_i - минимальное содержание питательного вещества i в кормовом рационе; С_i – цена за единицу корма j ( 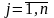). Система ограничений и функция цены в этом случае будут иметь вид:

x_j ≥ 0

Экономический смысл неравенств заключается в том, что кормовой рацион должен содержать все необходимые питательные вещества и при этом стоимость кормовой смеси должна быть минимальной (это задачи о смесях).

Любую из рассмотренных ранее задач линейного программирования можно свести к так называемой «общей задаче линейного программирования» (ОЗЛП), которая с использованием знака суммирования ∑ формулируется так: найти экстремум (максимум или минимум) линейной целевой функции f(x)

Max(min)f(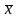 )= 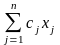(1.16)

при ограничениях (условиях):

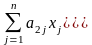(1.17)

. . . . . . . . . . . . . . . . .

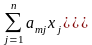
x_j ≥ 0, j= (1.18)

где а_ij, b_j, c_j (i= ; j= ) – заданные постоянные величины.

Ограничения (1.17) называют функциональными ограничениями ОЗЛП, а ограничения (1.18) – прямыми. Вектор = ( x₁, x₂, …, x_n), удовлетворяющий системе ограничений (1.17), (1.18) называется допустимым решением или планом ОЗЛП. План, при котором достигается max (min) целевой функции (1.16), называется оптимальным планом (оптимальным решением) ЗЛП.

Если все функциональные ограничения (1.17) имеют знак «≤», то задача линейного программирования называется стандартной (приведенной к стандартной форме). ОЗЛП приводится к стандартной форме умножением неравенств типа «≤» на (-1).

Канонической формой (видом) задачи линейного программирования (КЗЛП) называют задачу: найти =

при ограничениях:

x_i ≥ 0, b_i ≥ 0,

В линейной алгебре доказывается, что систему из r независимых уравнений с n переменными x₁, x₂, … ,x_n всегда можно разрешить относительно каких-то r переменных (называемых «базисными») и выразить их через остальные k = n – r переменные (называемые «свободными»).

Свободным переменным можно придать какие угодно значения, не нарушая условий (1.17). Так, например, для того, чтобы перейти от условий-равенств (1.17) к условиям-неравенствам, достаточно разрешить уравнения (1.17) относительно каких-то r базисных переменных, выразить их через свободные, а так как все переменные должны быть неотрицательными, то записывать условия их неотрицательности в виде ограничений-неравенств.

А потом «забыть» о базисных переменных и манипулировать только свободными, число которых будет k = n-r. При этом надо будет освободить от базисных переменных также и целевую функцию, подставив в нее выражения базисных переменных через свободные. Таким образом, при переходе от ОЗЛП к задаче с ограничениями-неравенствами число переменных не увеличивается, а уменьшается на число r независимых условий-равенств в ОЗЛП.

Переход от стандартной к канонической форме осуществляется введением дополнительных неотрицательных неизвестных – невязок неравенств. Например, от ограничений легко перейти к ограничениям в виде равенств , обозначив через x₃ и x₄ разности между правыми и левыми частями неравенств: x₃=1-(2x₁+x₂)

X₄=1-(x₁+5x₂)