14

Лекция 2 Динамика вращательного движения.

1.Неинерциальные системы отсчета.Силы инерции.

2.Движение тела с переменной массой.

3.Момент силы. Момент импульса.

4.Моменты инерции. Теорема Штейнера.

5.Основной закон динамики вращательного движения

6.Закон сохранения момента импульса.

7.Гироскопы.

8.Деформации.Закон Гука.

9.Тяготение. Элементы теории поля .Закон всемирного тяготения.1-я,2-я,3-я космические скорости

Неинерциальные системы отсчета.Силы инерции

Закон Ньютона для неинерциальных систем отсчета

где — силы инерции. Силы при этом должны быть такими, чтобы вместе с силами 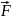, обусловленными воздействием тел друг на друга, они сообщали телу ускорение а', каким оно обладает в неинерциальных системах отсчета

а —ускорение тела в инерциальной системе отсчета.

Силы инерции это силы, обусловленные ускоренным движением системы отсчета, относи­тельно измеряемой системы отсчета.

Силы инерции вызываются не взаимодействием тел, а ускоренным движением системы отсчета. Поэтому они не подчиняются третьему закону Ньютона, так как если на какое-либо тело действует сила инерции, то не существует противодействующей силы, приложенной к данному телу.

Проявление сил инерции

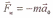1. Силы инерции при ускоренном поступательном движении системы отсчета.(Пример: они проявляются в перегрузках при запуске и спуске космических кораблей).

2. Силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета.

Сила F_цб— центробежная сила инерции,

,

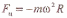ω = const — угловая скорость

Пример: их действию подвергаются пассажиры в движущемся транспорте на поворотах.

3. Силы инерции, действующие на тело, движущееся во вращающейся системе отсчета.

F_к — кориолисова сила инерции.

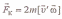
Вектор F_к перпендикулярен векторам скорости v' тела и угловой скорости вращения ω системы отсчета в соответствии с правилом правого винта

(Пример: в северном полушарии правые берега рек подмываются сильнее).

Основной закон динамики для неинерциальных систем отсчета:

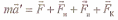
Движение тела переменной массы

Имеется много случаев, когда масса тела изменяется в про­цессе движения за счет непрерывного отделения или присоеди­нения вещества (ракета, реактивный самолет, платформа, на­гружаемая на ходу, и др.).

Найдем уравнение движения такого тела для материальной точки, называя ее для краткости телом. Пусть в некоторый момент t масса движущегося тела А равна m, а присоединяемое (или отделяемое) вещество имеет скорость u относительно данного тела.

Введем вспомогательную инерциальную K-систему отсчета, скорость которой такова же, как и скорость тела А в данный момент t. Это значит, что в момент t тело А покоится в K-системе.

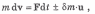Пусть далее за промежуток времени от t до t + dt тело А при­обретает в K-системе импульс mdv. Этот импульс тело А полу­чит, во-первых, вследствие присоединения (отделения) массы , которая приносит (уносит) импульс δm·u , и, во-вторых, вследствие действия силы F со стороны окружающих тел или силового поля. Таким образом,

где знак плюс соответствует присоединению массы, а знак минус — отделению. Оба эти случая можно объединить, представив ±δm в виде приращения dm- массы тела. Тогда предыдущее уравнение примет вид

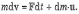
Разделив это выражение на dt, получим

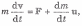
где u — скорость присоединяемого (или отделяемого) вещества относительно рассматриваемого тела.

Это уравнение является основным уравнением динамики точки переменной массы. Его называют уравнением Мещер­ского. Будучи полученным в одной инерциальной системе от­счета, это уравнение в силу принципа относительности справед­ливо и в любой другой инерциальной системе. Заметим, что если система отсчета неинерциальна, то под силой F следует понимать результирующую силу как сил взаимодействия дан­ного тела с окружающими телами, так и сил инерции.

Последнее слагаемое уравнения названо реактивной силой:

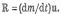
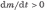Эта сила возникает в результате действия на даное тело присоединяемой (или отделяемой) массы. Если масса присоединяется т, ,вектор R совпа-дает по направлению с вектором u; если же масса отделяется, то вектор R противоположен вектору u.

Уравнение Мещерского по своей форме совпадает с основ­ным уравнением динамики материальной точки постоянной массы: слева — произведение массы тела на ускорение, спра­ва — действующие на него силы, включая реактивную силу. Однако в случае переменной массы нельзя внести массу m под знак дифференцирования и представить левую часть уравнения как производную по времени от импульса, ибо mdv/dt ≠ d(mv)/dt.

Обратим внимание на два частных случая:

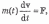1. Если u = 0, т. е. масса присоединяется или отделяется без скорости относительно тела, то R = 0 и уравнение Мещерского прини­мает вид

где m(t) — масса тела в данный момент времени. Это уравнение определяет, например, движение платформы, из которой сво­бодно высыпается песок.

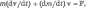2. Если u = - v, т. е. присоединяемая масса неподвижна в вы­бранной системе отсчета или отделяемая масса становится не­подвижной в этой системе, то уравнение Мещерского принимает дру­гой вид: или

Иначе говоря, в этом частном случае — и только этом — действие силы F определяет изменение импульса тела с пере­менной массой. Данный случай реализуется, например, при движении платформы, нагружаемой сыпучим веществом из неподвижного бункера .

Рассмотрим пример на применение уравнения Мещерского.

Пример. Ракета движется в инерциальной K-cистеме отсчета в отсут­ствие внешнего силового поля, причем так, что газовая струя испускается с постоянной относительно ракеты скоростью и. Найдем зависимость скорости v ракеты от ее массы m, если в момент старта ее масса была равна m₀.

В данном случае F = 0 и из уравнения Мещерского следует

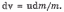
Проинтегрировав это выражение с учетом начальных усло­вий, получим

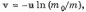
где знак минус показывает, что вектор v (скорость ракеты) противоположен по направлению вектору u. Отсюда видно, что скорость ракеты в данном случае (u = const) не зависит от времени сгорания топлива: v определяется только отношением начальной массы m₀ ракеты к оставшейся массе m.

Заметим, что если бы вся масса горючего была одновременно выброшена со скоростью u относительно ракеты, то скорость последней оказалась бы иной. Действительно, если ракета вначале покоилась в выбранной инерциальной системе отсчета, а после одновременного выброса всего горючего приобрела скорость v, то из закона сохранения импульса для системы ракета-горючее следует

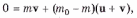
где (u + v) — скорость горючего относительно данной системы отсчета. Отсюда

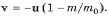
Скорость v ракеты в этом случае оказывается меньше, чем в предыдущем (при одинаковых значениях отношения m_о/m).

Момент инерции.

Момент инерции системы (тела) относительно оси вращения есть физическая величина, равная сумме произведений масс п материальных точек системы на

квадраты их расстояний до рассматриваемой оси:

В случае непрерывного распределения масс эта сумма сводится к интегралу

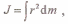
где интегрирование производится по всему объему тела. Величина г в данном случае есть функция положения точки с координатами х, у, z.

Теорема Штейнера

Момент инерции тела /относительно любой оси вращения равен моменту его инерции J_c относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы т тела на квадрат расстояния а между осями:

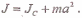
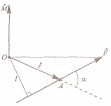
М омент силы относительно неподвижной точки о

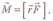
Физическая величина, определяемая векторным произведением радиуса-вектора г , проведенного из точки О в точку А приложения силы, на силу F (см. рисунок);

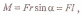Здесь М — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его враще­нии от r к F , Модуль момента силы

где α —угол между г и F; rsina = l —кратчайшее расстояние между линией действия силы и точкой О — плечо силы.

Момент силы относительно неподвижной оси z

Скалярная величина М, равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z (см, рисунок).

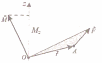Значение момента М. не зависит от выбора положения точки О на оси z. Если ось z совпадает с направлением вектора М, то момент силы представляется в виде вектора, совпадающего с осью:

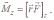
Кинетическая энергия вращения

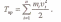Абсолютно твердое тело вращается вокруг неподвижной оси z. Разбивая тело на элементарные объемы массами m₁, m₂,..., m_п, находящиеся от оси на расстояниях г₁, г₂,..., г_n, запишем

Поскольку ω = v_l/r₁=v₂/r₂=:...= v_n/r_n,

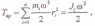
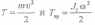где J_z — момент инерции тела относительно оси z. Из сравнения формул

следует, что момент инерции — мера инертности тела при вращательном движении.

Уравнение динамики вращательного движения твердого тела

Работа вращения тела идет на увеличение его кинетической энергии:

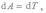
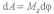
( М_z — момент сил относительно оси z),

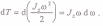
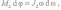
Тогда

или

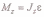Учитывая, что ω = 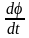получаем

— уравнение динамики вращательного движения твердого тела относительно неподвижной оси.

Если ось вращения совпадает с главной осью инерции, проходящей через

центр масс, то имеет место векторное равенство

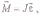
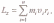
где J -главный момент инерции тела (момент инерции относительно главной оси).

Момент импульса относительно неподвижной точки о

Физическая величина, определяемая векторным произведением

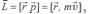
где r— радиус-вектор, проведенный из точки О в точку А;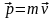 -импульс материальной точки; L-псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от г к р.

Момент импульса относительно неподвижной оси

Это скалярная величина L, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Значение момента импульса L. не зависит от положения точки О на оси z.

Закон сохранений момента импульса

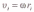Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц . Учитывая, что

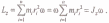
получим

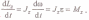
Продифференцируем уравнение по времени:

Можно показать, что имеет место век­торное равенство

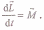
Это выражение — еще одна форма уравнения (закона) динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси. В замкнутой системе момент внешних сил М = 0 и 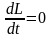, откуда

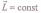
— закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени. Это — фундаментальный закон природы. Он является следствием изотропности пространства: инвариантность физических законов относительно выбора направления осей координат системы отсчета.