1.3. Операции над событиями

Определение 3. Если всякий раз, когда происходит событие А в данном опыте происходит и событие В, то говорят, что А влечет за собой событие В и пишут .

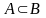П роиллюстрируем это понятие на схематичном рисунке.

Пример 5. При бросании игральной

кости рассмотрим два события:

1. А  выпадение четырёх очков; А В

2. В  выпадение четного числа очков.

Тогда , т.е. событие А влечет E

за собой событие В.

Если же и 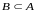, то .

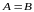О пределение 4. Суммой двух событий

А и В называется событие А B

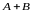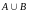или , состоящее

в появлении по крайней мере A + B

одного из событий А или В. E

Определение 5. Произведением двух событий А и В называется со-бытие или , состоящее в одновременном появлении событий А и В.

П ример 6. Опыт состоит в подбрасы-

вании двух монет:

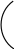А  выпадение герба на первой монете; А В

В выпадение герба на второй монете.

Тогда  выпадение хотя бы E

одного герба,  выпадение двух гербов одновременно.

Определение 6. Разностью двух событий А и В называется событие 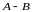или , состоящее в появлении события А без события В.

П ример 7. Брошена игральная кость.

Рассмотрим два события: А В

А  выпадение четного числа очков;

В  выпадение двух очков.

Тогда событие  выпадение E

четырёх или шести очков.

Определение 7. Событие Е называется достоверным событием, т.е. это такое событие, которое в результате опыта непременно произойдёт.

Определение 8. Пустое множество называется невозможным событием, т.е. это событие, которое в данном опыте не может произойти.

О пределение 9. Событие

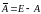
называется событием, противоположным

событию А. Событие 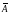означает, А

что событие А не произошло.

E

Определение 10. События А и В называются несовместными событиями, если 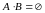. Это означает, что наступление А исключает появление В.

П ри этом .

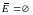Пример 8. Брошена монета.

Рассмотрим два события: А В

А  появление герба;

В  появление цифры. E

Очевидно, что А и В  несовместные события.

Определение 11. События образуют полную группу событий, если:

1. Они попарно несовместны, т.е. ;

2. .

Пример 9. Брошена игральная кость. Тогда события 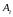 появление “i” очков 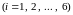образуют полную группу событий.

Пример 10. .
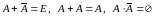