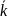- •Федеральное государственное образовательное учреждение высшего профессионального образования
- •Лекция 1. Введения в теорию статистических решений.
- •Лекция 2. Принципы принятия статистических решений.
- •1. Байесовский принцип
- •1) Метод минимального числа ошибочного решений:
- •2) Метод наибольшего правдоподобия.
- •Лекция 3. Минимаксный принцип
- •1)Сущность минимаксного принципа.
- •2)Формирование решающего правила
- •Лекция 4. Статические гипотезы.
- •Основные этапы проверки статистических гипотез
- •Лекция 5. Проверка статистических гипотез о законах распределения.
- •Лекция 6 Проверка статистических гипотез о числовых характеристиках случайных величин
- •2. Статистические гипотезы о дисперсиях
- •Лекция 7. Оценивание свойств изделий по результатам испытаний.
- •Лекция 8. Методы получения интервальных оценок
- •Лекция 9. Случайные процессы.
- •1. Характеристики и свойства случайных процессов.
- •Лекция 10. Исходные понятия теории статистического анализа
- •Лекция 11. Дисперсионный анализ.
- •Лекция 12. Корреляционный анализ
- •Лекция 13. Регрессионный анализ
- •Лекция 14 Полный факторный эксперимент
- •Лекция 15. Дробный факторный эксперимент
- •Лекция 16. Проведение эксперимента
- •Лекция 17. Обработка результатов эксперимента (заключительные этапы регрессионного анализа).
Лекция 13. Регрессионный анализ
1). Назначение и сущность регрессионного анализа. Классификация по видам.
2). Планирование эксперимента. Как метод реализации процедуры РА. Критерии оптимальности планов.
Назначение и сущность регрессионного анализа. Классификация по видам.
Регрессионным анализом называется один из видов статистического анализа, представляющий собою совокупность методов обработки результатов испытаний, зависящих от различных одновременно действующих случайных факторов различной природы, с целью построения уравнения регрессии в интересах исследования стохастической взаимосвязи между откликом и факторами.
Таким
образом, исходная предпосылка заключается
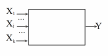
в том, что между случайным откликом Y
и случайным вектором факторов X
существует стохастическая зависимость
вида
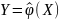 ,
где
,
где
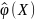 в общем случае может быть как случайной,
так и неслучайной функцией случайных
аргументов, вид которой неизвестен.
Если бы была известна зависимость закона
распределения Y от
вектора X, то она
позволила бы провести всесторонний
анализ стохастической взаимосвязи Y
и X. Такой путь решения
задачи в принципе возможен, но как
свидетельствует опыт исследований, не
всегда целесообразен. В практике
испытаний гораздо чаще используется
другой вариант решения, идея которого
заключается в том, чтобы установить
зависимость какой-либо числовой
характеристики Y от
возможных значений компонент вектора
X в виде неслучайной
функции неслучайных аргументов. В
регрессионном анализе в качестве такой
числовой характеристики используется
условное математическое ожидание
отклика Y, определяемое
при условии, что компоненты вектора X
приняли определенные значения:
в общем случае может быть как случайной,
так и неслучайной функцией случайных
аргументов, вид которой неизвестен.
Если бы была известна зависимость закона
распределения Y от
вектора X, то она
позволила бы провести всесторонний
анализ стохастической взаимосвязи Y
и X. Такой путь решения
задачи в принципе возможен, но как
свидетельствует опыт исследований, не
всегда целесообразен. В практике
испытаний гораздо чаще используется
другой вариант решения, идея которого
заключается в том, чтобы установить
зависимость какой-либо числовой
характеристики Y от
возможных значений компонент вектора
X в виде неслучайной
функции неслучайных аргументов. В
регрессионном анализе в качестве такой
числовой характеристики используется
условное математическое ожидание
отклика Y, определяемое
при условии, что компоненты вектора X
приняли определенные значения:
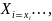
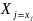 ….,
….,
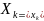 ….
….
Следовательно, в РА используется зависимость вида:
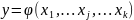 (13.1)
(13.1)
где:
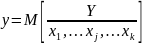 ,
,
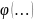 - неслучайная функция неслучайных
аргументов.
- неслучайная функция неслучайных
аргументов.
Эта зависимость предназначена для того, чтобы приближенно представлять истинную стохастическую взаимосвязь между откликом и факторами, т.е. она является регрессией отклика на факторы.
Таким образом, в представлении соотношения в виде (13.1) заключается сущность РА, а в построении зависимости (13.1) по результатам испытаний – его цель.
Различают однофакторный и многофакторный, одномерный и многомерный РА, а по виду зависимости – линейный и нелинейный.
В линейном РА зависимость (1) представляют в виде полинома:
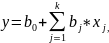
где
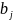 - оценка коэффициентов регрессии
- оценка коэффициентов регрессии
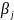 (
(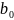 – оценка для
– оценка для
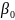 ).
).
В нелинейном РА зависимость (13.1) обычно включает члены, представляющие так называемые эффекты взаимодействия и степенные эффекты, т.е. члены вида
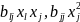 и т.д.
и т.д.
Активный и пассивный эксперимент.
Исходные понятия ТПЭ: фактор, отклик, план эксперимента.
Отклик Y – однокомпонентный вектор. Фактор X – многокомпонентный вектор столбец вида:
X=
|
|
В каждом опыте участвуют все факторы, так что в i-м опыте имеем:
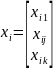 ;
;
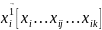
Всего
опытов N, т.е. i
= 1,
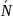
Матрицей спектра плана эксперимента называется матрицы вида:
X
=
 =
=
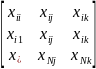
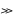 N точек с координатами
(
N точек с координатами
(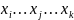 )
)
Совокупность всех точек в пространстве k факторов, отличающихся уровнями хотя бы одного фактора, называется спектром плана эксперимента.
Опыт в i-х условиях может повторяться n раз, что можно представить матрицей дублирования опытов :
=
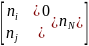
Матрица спектра совместно с матрицей дает план эксперимента, совокупность данных, определяющих число, условия и порядок реализации опытов.
ПЭ:
точный,
если
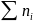 задана;
задана;
насыщенный,
если N=k
(без учёта
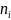 )
)
регулярный,
если
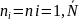
Разработка плана эксперимента (ПЭ):
Определение пространства факторов
Выбор стратегии испытания

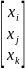 ,
j=1,
,
j=1,