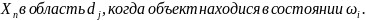Федеральное государственное образовательное учреждение высшего профессионального образования
«БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ «ВОЕНМЕХ» ИМ. Д.Ф. УСТИНОВА»
(БГТУ «ВОЕНМЕХ» им. Д.Ф. УСТИНОВА)
________________________________________________________________
В.И.Запорожец, В.В.Шикурин
“Испытания изделий”
Тексты лекций
Санкт-Петербург
2015г
Оглавление
Лекция 1. Введения в теорию статистических решений. 3
Лекция 2. Принципы принятия статистических решений. 6
Лекция 3. Минимаксный принцип 10
Лекция 4. Статические гипотезы. 14
Лекция 5. Проверка статистических гипотез о законах распределения. 22
Лекция 6 Проверка статистических гипотез о числовых характеристиках случайных величин 30
Лекция 7. Оценивание свойств изделий по результатам испытаний. 39
Лекция 8. Методы получения интервальных оценок 44
Лекция 9. Случайные процессы. 50
Лекция 10. Исходные понятия теории статистического анализа 55
Лекция 11. Дисперсионный анализ. 62
Лекция 12. Корреляционный анализ 68
Лекция 13. Регрессионный анализ 74
Лекция 14 Полный факторный эксперимент 77
Лекция 15. Дробный факторный эксперимент 86
Лекция 16. Проведение эксперимента 92
Лекция 17. Обработка результатов эксперимента (заключительные этапы регрессионного анализа). 98
Лекция 1. Введения в теорию статистических решений.
1). Предмет и задачи дисциплины. Исходные понятия теории испытаний.
2). Постановка задачи выработки статистических решений.
Общие положения
Под испытанием технических изделий подразумевается процесс определения их работоспособности (пригодности по целевому назначению) и/или определения их характеристик опытным путем.
В общем случае процесс испытаний включает четыре основных этапа:
- планирование испытаний,
- проведение испытаний,
- обработка результатов испытаний и принятие решений по результатам испытаний.
Изучаемая дисциплина посвящена основам формирования решений. Она имеет объем 68 учебных часов, которые распределены следующим образом: 34 часа лекционных и 34 часа практикум. Из 34 часов практикума 28 отводится на лабораторные работы (4 работы по 7 часов); 4 часа на прием лабораторных работ и 2 часа на зачет с оценкой.
Теоретической базой дисциплины является теория вероятностей.
Справка по исходным понятиям теории вероятности:
случайное событие – факт, который в результате опыта может произойти или не произойти;
вероятность – количественная мера случайности (вероятности проявления события);
случайная величина и её реализации;
характеристики случайной величины:
закон распределения (исчерпывающая),
числовые характеристики (моменты).
Вероятность события есть численная мера объективной возможности проявления этого события.
Событие - всякий факт, который в результате опыта может произойти или не произойти.
Полная группа событий, если в результате опыта непременно должно проявиться хотя бы одно из них.
Вероятность, как мера необходимая для количественного сравнения событий по степени возможности их проявления.
Вопросы по теории вероятностей, необходимые для освоения курса «Испытание изделий»:
1. Случайное событие. Вероятность события. Полная группа событий. Несовместные события. Равновозможные события.
2. Случайная величина. Дискретные и непрерывные СВ. Характеристики СВ:
1) закон распределения (определение, виды (формы) закона: табличный, графический, аналитический);
плотность распределения, функция распределения, взаимосвязь между ними;
2) числовые характеристики СВ (начальные и центральные моменты СВ);
3) характеристики положения (мода, медиана);
3. Основные теоремы вероятностей (сумма и произведение событий, теорема сложения вероятностей, теорема умножения вероятностей, формула полной вероятности, теорема гипотез - формула Байеса).
Постановка задачи выработки статистических решений
В рассмотрение вводятся:
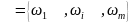– множество возможных состояний объекта;
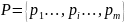- множество вероятностей состояния
объекта;
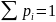
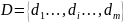– множество решений;
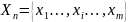– выборка по результатам испытаний;
Полагаются известными:
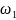f(x/
)=
f(x/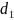
)-
закон исследуемого параметра;
С(
.
Формулировка
задачи: известны множества 
,
,
,
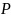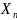а также закон f(x/
),
функция потерь С(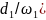
,
правило принятия решения и сформированный
на его основе критерий; требуется принять
решение на множестве D.
Примечание: правило принятия решений есть зависимость, устанавливающая соответствие между принимаемым решением и возможным состоянием объекта ; эта зависимость называется оценочным функционалом.
В рассмотрение вводятся:
, P, D
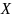−признак,
f(x/ )
Хn
Cij
R - оценочный функционал
Формулировка задачи: принять решение на множестве D, с учетом всей вышеперечисленной исходной информации.
В общем случае оценочный функционал R определяется зависимостью:
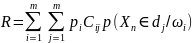
Где
Р(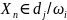
)
– условная вероятность попадания
выборки
