Шпаргалка По Физике (Штеренберг А. М.) / 28.Затухающие гармонические колебания

28.Затухающие гармонические колебания.

Затухающие гармонические колебания - амплитуда которых, вследствие потери энергии в реальной системе, с течением времени уменьшается.

dx²/dt² + 2δ dx/2t + ω₀²x = 0

δ = r/2m - коэффициент затухания, характеризующий быстроту убывания амплитуды,

Затухающие колебания не являются истинно периодическим процессом, т.к. в них никогда не повторяются значения физических величин.

Условным периодом затухающих колебаний наз. промежуток времени между двумя состояниями колеблющейся системы, в которых физические величины, характеризующие колебания, принимают аналогичные значения, изменяясь в одном и том же направлении: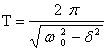 , где w0 – собственная частота свободных колебаний.

При условии d < w0 затухающие колебания описываются уравнением ,где .

Если d > w0, то трение в системе очень велико и колебаний не происходит, запас механической энергии тела к моменту его возвращения в положение равновесия полностью расходуется на преодоление трения.

Логарифмический декремент затухания подставим A(t) = A₀^-βt.

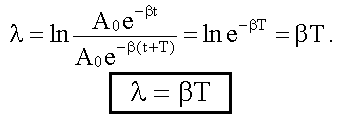
Время релаксации - это время τ, за которое амплитуда уменьшилась в e=2,7... раз, т.е.  , тогда   . Т.к.    - число колебаний за время , то:

Добротность