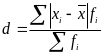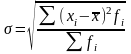Пример решения задачи 2.

Для трех крупных предприятий одного из районов города известны следующие данные:

Таблица 2.3-Данные для расчета средней величины

Предприятия	Численность рабочих, чел. (Ч)	Производительность труда 1 работника, тыс. руб. на 1 человека (В)
1	318	165
2	441	220
3	520	381

Определите среднюю производительность труда по району. Укажите вид и форму средней величины.

Решение.

1)Производительность труда – вторичный признак, представляющий собой соотношение стоимости произведенной продукции и численности работников.

Логическая формула:

, где стоимость произведенной продукции.

2) По условию задачи неизвестна стоимость произведенной продукции, то есть числитель логической формулы, значит расчет средней производительности труда проводим по схеме средней арифметической взвешенной.

; С –неизвестна.

Выражаем С через известные признаки: С =В*Ч. Подставим это выражение в исходное равенство:

Получим :

- для одного предприятия ;

-для совокупности предприятий:

тыс.руб. на 1 чел.

Средняя производительность труда 2 работника по району города составила в среднем 266,8 тыс.руб. на 1 чел. При расчете использована средняя арифметическая взвешенная.

3. При решении задачи 3 необходимо:

1. Перейти от интервального ряда к дискретному, рассчитав середины интервалов как полусуммы границ.

2. Рассчитать накопленную частоту (F_i) по каждому интервалу, равную сумме частот всех предшествующих интервалов, включая данный.

3. Графически изобразить интервальный вариационный ряд в виде ряда прямоугольников, построенных на оси Х. Их ширина равна длине интервала, а высота соответствующей частоте. Такой график называется гистограммой распределения. Если середины верхних сторон прямоугольников соединить прямыми, то можно получить полигон распределения, площадь которого соответствует площади гистограммы.

4. Рассчитать среднее значение интервального ряда по формуле:

, где х_i-середина интервала, f_i-частота интервала.

5. Вычислить моду и медиану, характеризующие центр изучаемого распределения по следующим формулам:

Мода:

где:

- нижняя граница модального интервала (интервала с наибольшей частотой),

- длина модального интервала

- частота интервала, соответственно предшествующего модальному, модального и следующего за модальным.

Медиана:

где:

- нижняя граница медианного интервала. У медианного интервала кумулятивная частота равна или превышает половину суммы частот.

- длина медианного интервала

- накопленная частота, предшествующая медианному интервалу.

-сумма всех частот.

-частота медианного интервала.

6. Рассчитать показатели вариации, характеризующие разброс значений изучаемого признака вокруг средней величины по следующим формулам:

Таблица 2.4 - Формулы для расчета показателей вариации

Показатель	Формула
Среднее линейное отклонение
Дисперсия
Среднее квадратическое отклонение
Коэффициент вариации

где:

х_i-середина интервала,

f_i-частота интервала

Если значение коэффициента вариации не превышает 50%, то вариация значений находится в пределах нормы. Если оно составляет более 50%, то совокупность неоднородна, средняя не надежна, необходимо с помощью типологической группировки выделять частные совокупности и изучать вариацию внутри данных групп.