
- •1. Линейная алгебра
- •1.10. Решить уравнение: .
- •1.6. Вычислить определитель
- •1.16. Решить системы линейных уравнений по формулам Крамера:
- •1.18. Решить слу методом Гаусса:
- •2. Векторная алгебра
- •4. Введение в анализ
- •Занятие 7. Алгебраические пределы
- •Занятие 8. Замечательные пределы. Эквивалентные бесконечно малые
- •Занятие 9. Непрерывность функции
1. Линейная алгебра
Умножение матриц. Обратная матрица |
|
|
|
В |
|
|
|
Решение СЛАУ. Формулы Крамера |
|
|
|
Занятие 1. Определители. Операции над матрицами
1.1.
Вычислить определитель
![]()
Устно. Вычислить определители:
|
1.3. Решить уравнение:
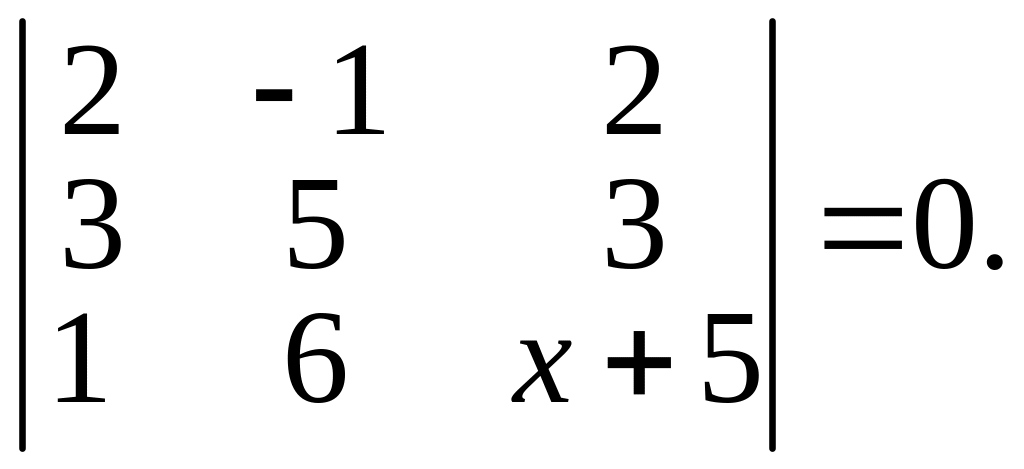
Устно. 1. Выполнить действия
2.
Найти
|
1.5. Дано:

Выполнить
действия (если возможно):
![]()
Домашнее задание. (5шт)
1.9.
Решить
неравенство:
![]() .
.
1.10. Решить уравнение: .
1.11а.
Вычислить определитель:
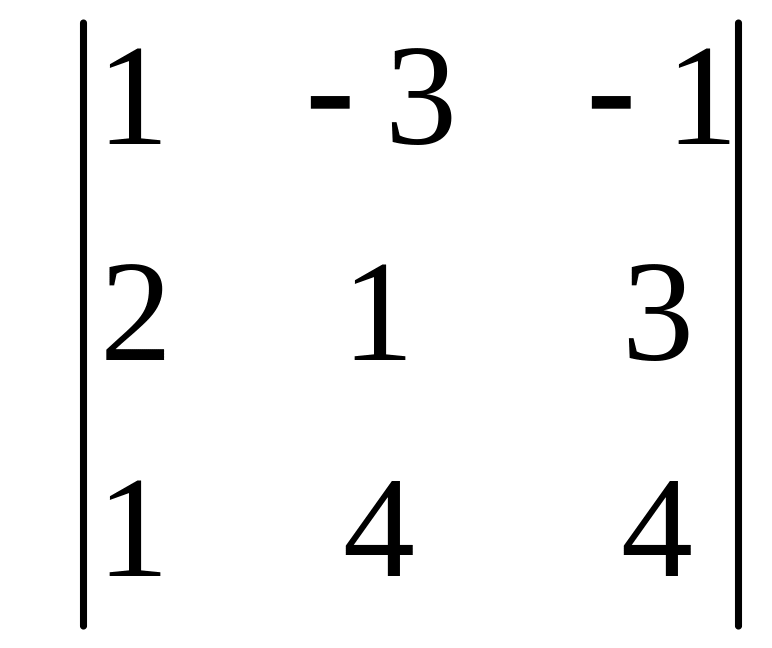
1.12.
Дано:
 ;
;
 .
Найти АВ–ВА.
.
Найти АВ–ВА.
1.13.
Дано:
 Найти
Найти
![]() .
.
Занятие 2
Устно.
Вычислить определитель разложением
по 1-й строке:
|
1.6. Вычислить определитель
1.7. Определить, существует ли матрица, обратная к данной. Если да – найти обратную матрицу.
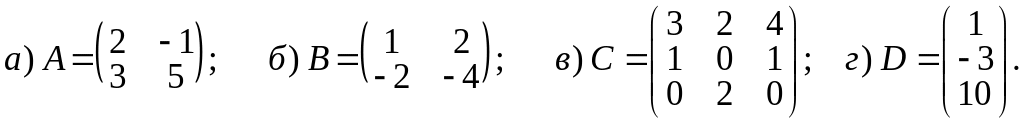
1.8.
Найти матрицу
![]() :
:
а)
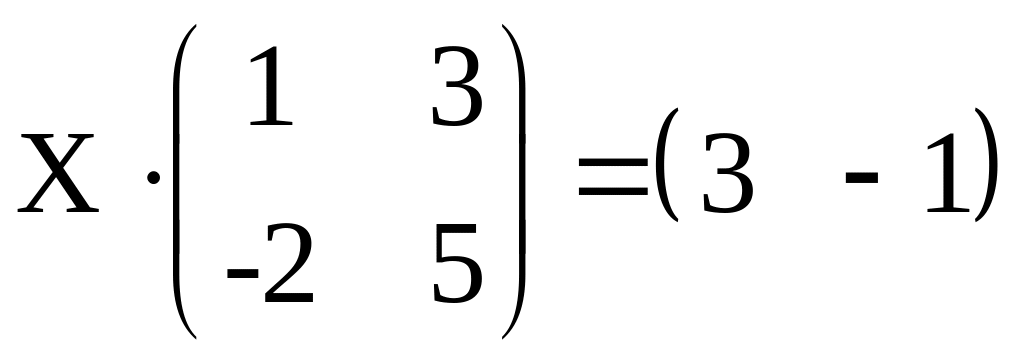 ;
б)
;
б)
 .
.
Домашнее задание. (2шт)
1.11б.
Вычислить определитель
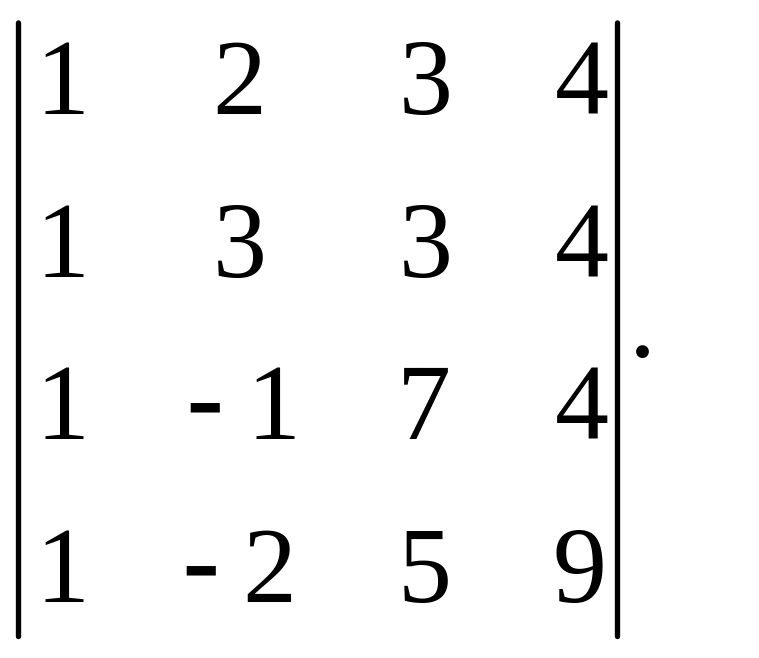
1.11в. Найти матрицы, обратные к данным и сделать проверку.
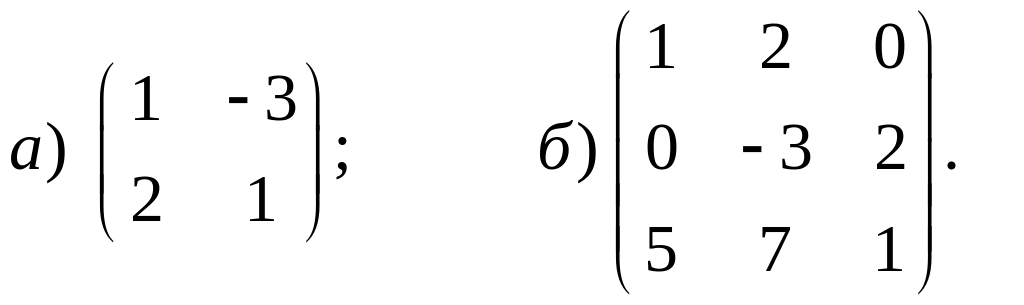
Ответы.
1.1.
6. 1.3.
-4. 1.5.
а)
действие невыполнимо; б)
![]() в)
действие невыполнимо;
г)
в)
действие невыполнимо;
г)
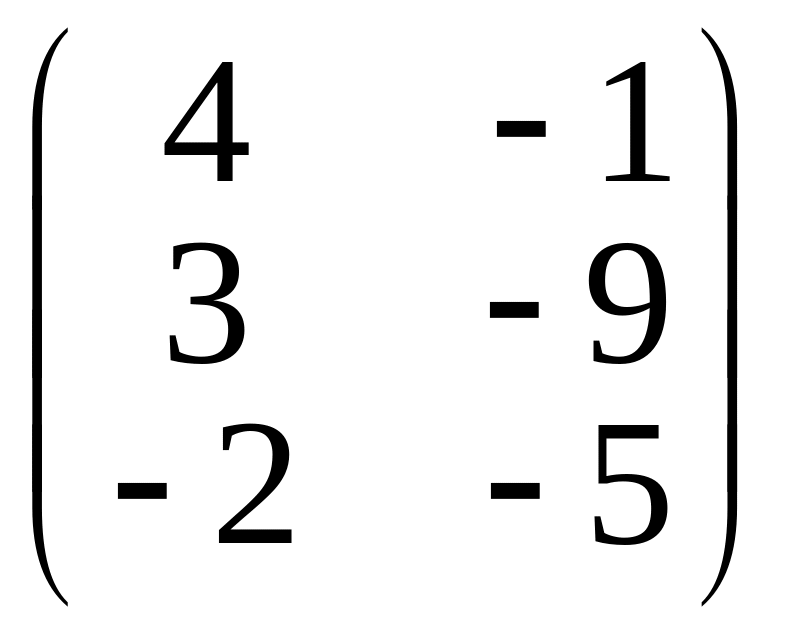 ;
д)
;
д)
![]() ;
е)
(-4);
ж)
;
е)
(-4);
ж)
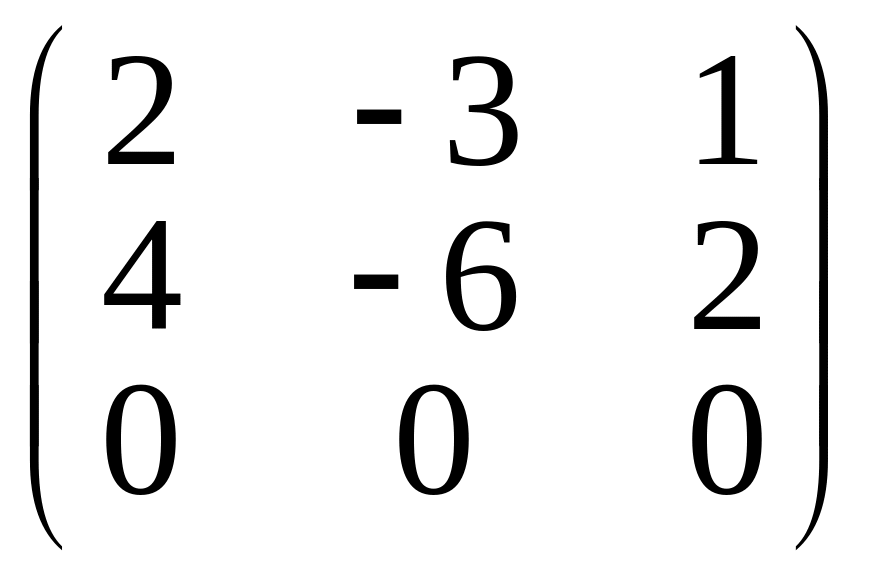 .
1.6.
-9.
.
1.6.
-9.
1.7.
а)
![]() ;
б)
не существует; в)
;
б)
не существует; в)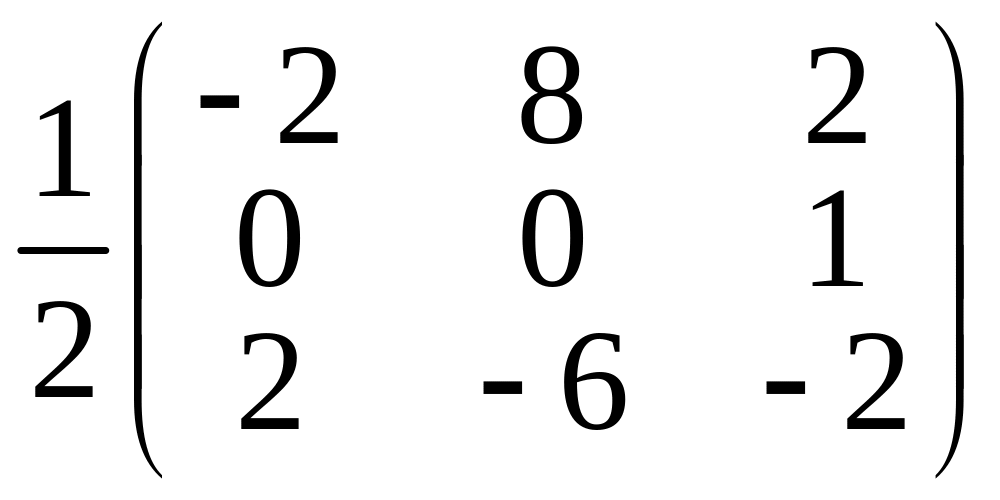 ;
г)
не существует.
;
г)
не существует.
1.8.
а)
![]() ;
б)
;
б)
![]() 1.9.
1.9.
![]() .
1.10.
.
1.10.
![]() .
.
1.11а)
0; 1.11б)
20.
1.12. .
1.13.
.
1.13.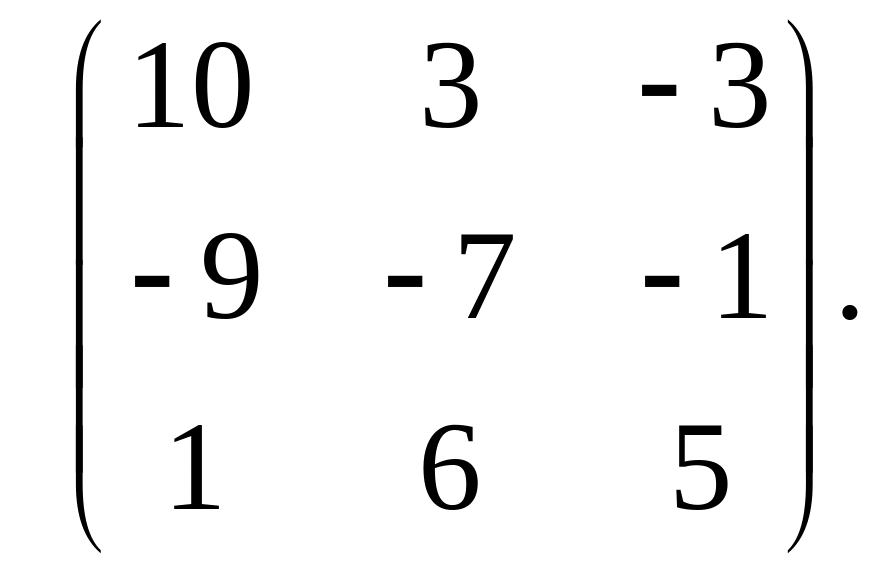
Занятие 3. Решение СЛАУ
1.14. Решить системы линейных уравнений по формулам Крамера:
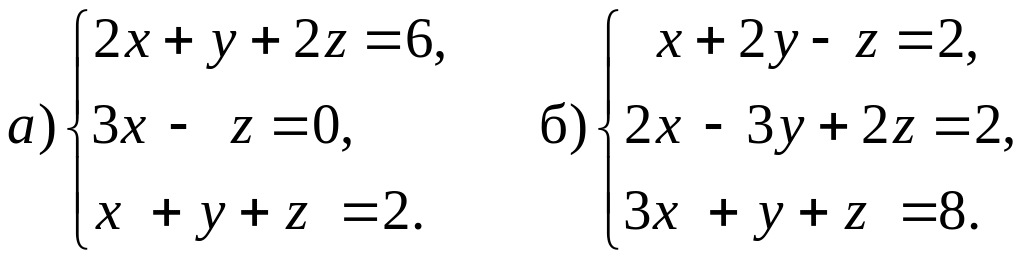
1.15. Решить СЛУ методом Гаусса:
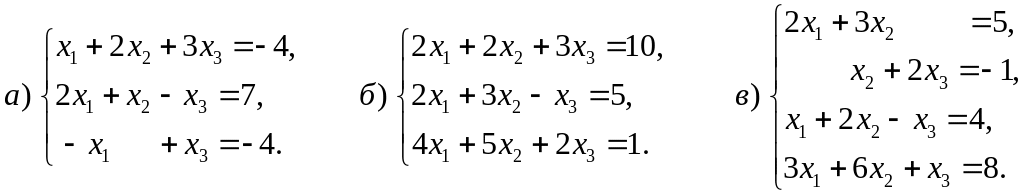

Домашнее задание. (7шт)
1.16. Решить системы линейных уравнений по формулам Крамера:

1.17.
Применяя формулы Крамера, найти
![]() из системы:
из системы:
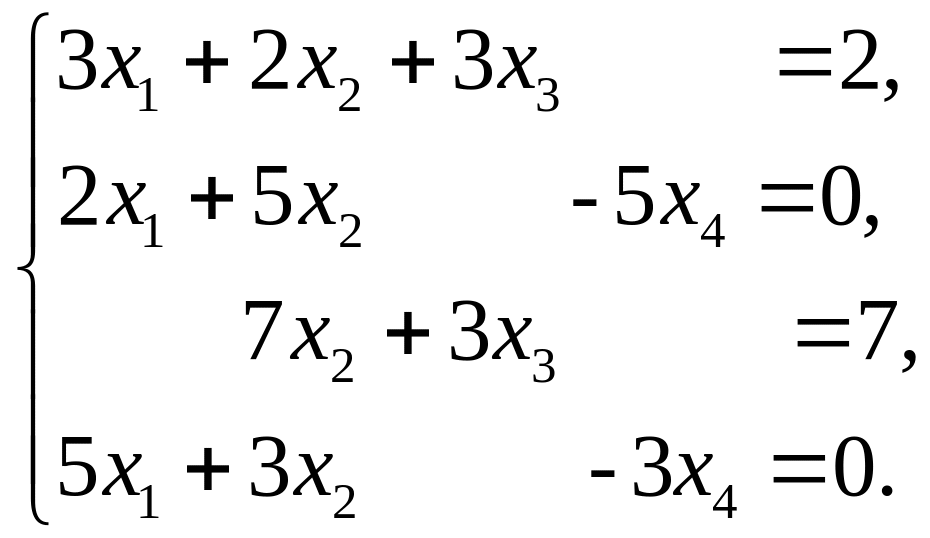
1.18. Решить слу методом Гаусса:
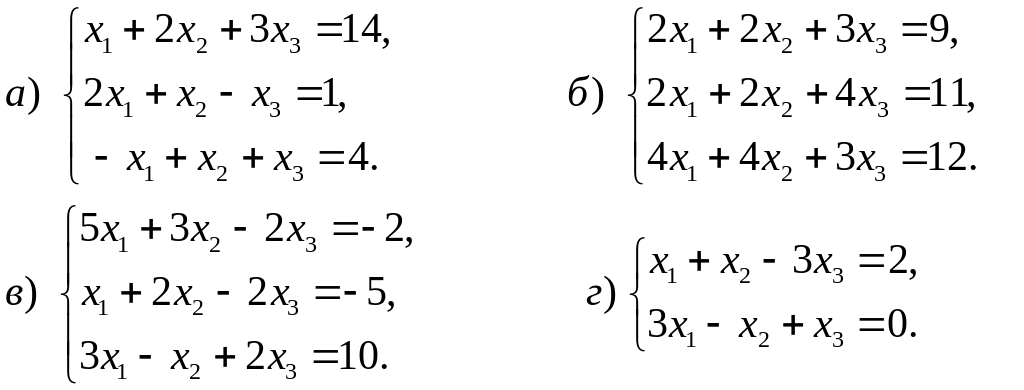
Ответы.
1.14.
а)![]() ;
б)
;
б)![]() .
1.15.
а)
.
1.15.
а)
![]() ;
б)
система
несовместна; в)
;
б)
система
несовместна; в)![]() ;
;
г)
![]() ;
д)
;
д)![]() .
.
1.16.
а)![]() ;
б)
;
б)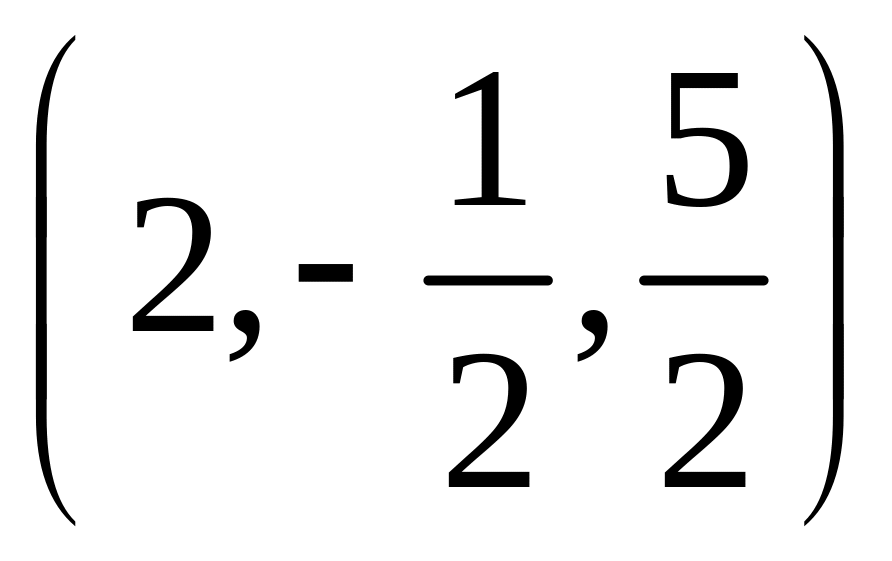 .
1.17. 1.
1.18.
а)
.
1.17. 1.
1.18.
а)![]() ;
б)
;
б)
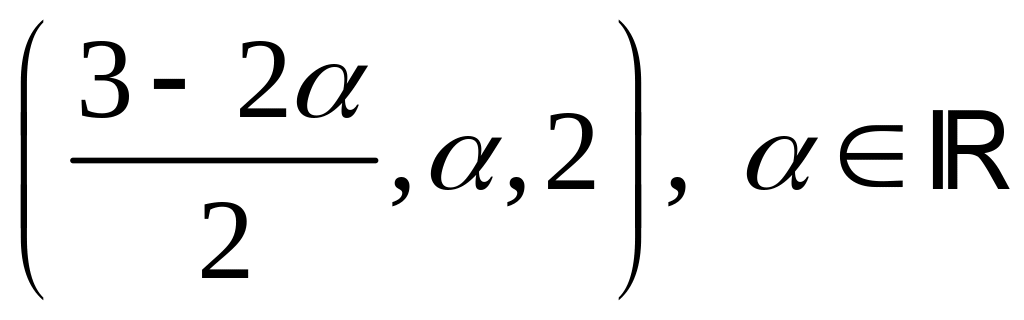 ;
;
в)
система
несовместна; г)
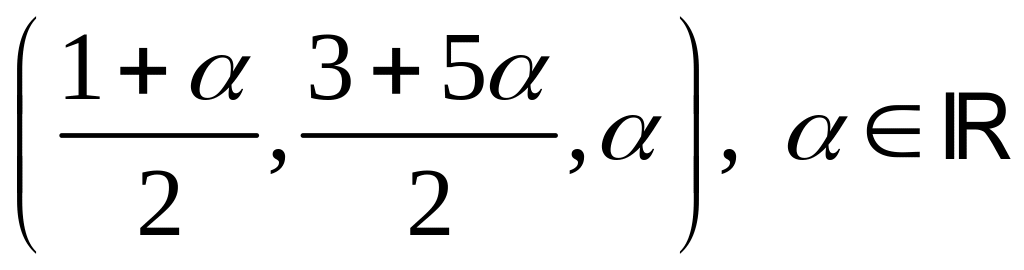 .
.
Задания для СРС. Решение СЛУ матричным методом. (3шт) 1. Решить системы линейных уравнений матричным методом:
Ответы. 1.
а) |
2. Векторная алгебра
|
|
|
|
|
||
середина
отрезка расстояние
между точками
|
|
Линейные
операции коллинеарность |
||||
Скалярное произведение (ЧИСЛО) |
Векторное произведение (ВЕКТОР) |
Смешанное произведение (ЧИСЛО) |
|
|
|
Занятие 4. Линейные операции над векторами
2.1.
В треугольнике ABC
:
![]() построить
построить
![]()
2.2.
В параллелепипеде
![]()
![]() .
.
Построить
![]()
Устно. Коллинеарны ли векторы:
|
2.3.
При каких значениях
![]() векторы
векторы
![]() и
и
![]() коллинеарны?
коллинеарны?
Устно.
Найти координаты вектора
|
|
в
1
Х
1
A
|
г
|
2.4.
Даны две вершины параллелограмма:
![]() и точка пересечения его диагоналей
и точка пересечения его диагоналей
![]() .
Определить две другие вершины.
.
Определить две другие вершины.
Устно.
Дано:
|
2.5.
Дано:
![]() .
Найти разложение вектора
.
Найти разложение вектора
![]() по базису
по базису
![]() .
.
2.6.
Найти орт и направляющие косинусы
вектора
![]() .
.
Домашнее задание. (4 шт)
2.7.
Известно:![]() .
Найти координаты точки
.
Найти координаты точки
![]() .
.
2.8.
Точка О – центр масс треугольника АВС.
Найти
![]() .
.
2.9.
Дано:
![]() ,
,
![]() .
Разложить вектор
.
Разложить вектор
![]() по базису
по базису
![]() .
.
2.10.
Известно, что вектор
![]() составляет острые углы с осями координат.
С осью ОХ
составляет острые углы с осями координат.
С осью ОХ
![]() ,
с
осью
OZ
,
с
осью
OZ
![]() .
Найти его координаты, если
.
Найти его координаты, если
![]() .
.
Ответы.
2.3.
![]() 2.4.
2.4.
![]() .
2.5.
.
2.5.![]()
2.6.
 .
2.7.
.
2.7.![]() .
2.8.
.
2.8.
![]() .
.
2.9.![]() 2.10.
2.10.
 .
.
Занятие 5. Скалярное и векторное произведение
Устно.
1) Найти скалярное произведение
векторов
2)
Найти длины векторов:
3)
При каком значении
|
2.11.
Дано:
![]() .
Вычислить
.
Вычислить
![]() .
.
2.12.
Векторы
и
![]() образуют угол
образуют угол
![]() ,
зная, что
,
зная, что
![]() .
Вычислить угол между диагоналями
параллелограмма, построенного на
векторах
и
.
.
Вычислить угол между диагоналями
параллелограмма, построенного на
векторах
и
.
2.13.
На материальную точку действуют силы
![]() .
Найти работу равнодействующей этих
сил
.
Найти работу равнодействующей этих
сил
![]() при перемещении точки из положения
при перемещении точки из положения
![]() в положение
в положение
![]() .
.
2.31.
Найти площадь параллелограмма,
построенного на векторах
![]() и
и
![]() ,
где
,
где
![]() ,
,
![]() и
и
![]() .
.
Устно.
Дано:
|
2.32.
Даны точки
![]() .
Вычислить площадь треугольника АВС
и
длину высоты
.
Вычислить площадь треугольника АВС
и
длину высоты
![]() .
.
Домашнее задание. (7шт)
2.14.
Дано:
![]() .
Найти модуль вектора
.
Найти модуль вектора
![]() .
.
2.15.
Даны вершины треугольника
![]() .
Определить его внутренний угол при
вершине В.
.
Определить его внутренний угол при
вершине В.
2.40.
Дано:
![]() .
Вычислить
.
Вычислить
![]() .
.
2.42.
Даны последовательно координаты вершин
параллелограмма:![]() .
Найти площадь параллелограмма
.
Найти площадь параллелограмма
![]() и длину высоты
и длину высоты
![]() .
.
2.43.
Силы
![]() приложены к точке
приложены к точке
![]() .
Найти величину и направляющие косинусы
момента равнодействующей этих сил
относительно точки
.
Найти величину и направляющие косинусы
момента равнодействующей этих сил
относительно точки
![]() .
.
2.44.
При каком значении
![]() компланарны векторы
компланарны векторы
![]() ?
?
2.45.
Даны вершины тетраэдра:
![]() .
Найти: а) угол
.
Найти: а) угол
![]() ;
б) площадь основания
;
б) площадь основания
![]() в)
объем тетраэдра
в)
объем тетраэдра
![]() ;
;
г)
длину высоты тетраэдра
![]() .
.
Ответы.
2.11.
–11. 2.12.
![]() 2.13. 1. 2.14.
2.13. 1. 2.14.
![]() .
2.15.
.
2.15.
![]() .
2.31. 25. 2.32. 14 ,
.
2.31. 25. 2.32. 14 ,
![]() .
2.40.
.
2.40.
![]() .
2.42.
.
2.42.
![]() .
2.43.
.
2.43.
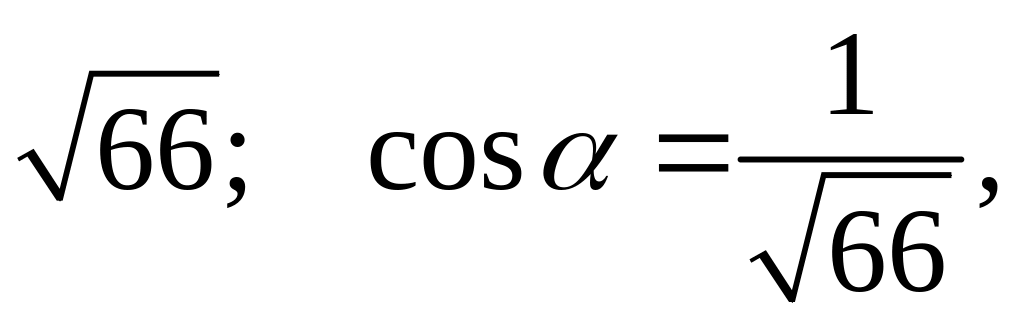
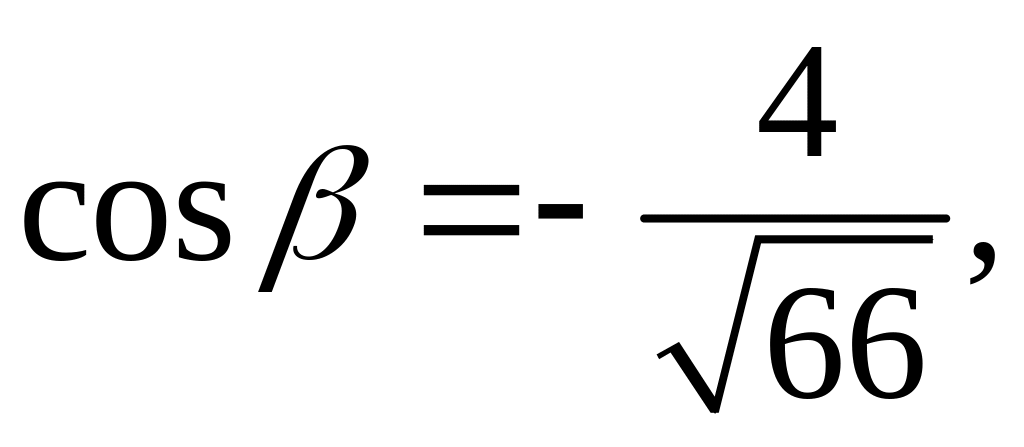
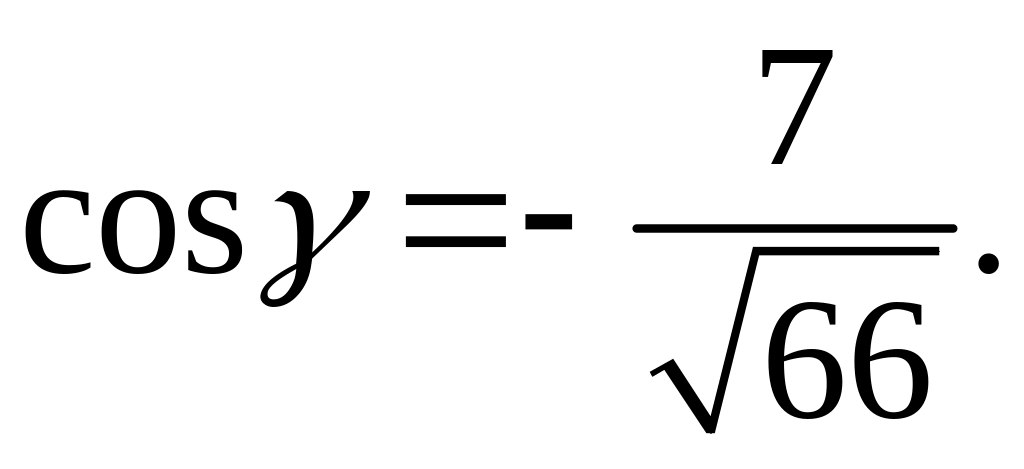 2.44.
2.44.
![]() .
2.45.
.
2.45.
![]()
ЗАДАНИЕ ДЛЯ СРС. Смешанное произведение. 1.
Лежат ли точки
2.
Векторы
,
и
3.
Даны вершины тетраэдра
Ответы. 1. да. 2. 24. 3. 11. |
Занятие 6. Контрольная работа «Линейная и векторная алгебра»
Вариант контрольной работы «Элементы линейной матрицы». Задание
1.
Матричным
методом найти y
из системы:
Задание
2. Решить систему линейных уравнений
В случае если система совместна, выполнить проверку. Задание
3. По формулам Крамера найти х
из системы
Задание
4. Решить матричное уравнение
Е - единичная матрица соответствующего порядка. Ответы. |
||||||
Вариант контрольной работы «Элементы векторной алгебры». Задание
1.Дано:
Задание
2. Найти орт и направляющие косинусы
вектора
(см. чертеж).
Задание
3. Дано:
Задание
4.
Найти
разложение вектора
|
||||||

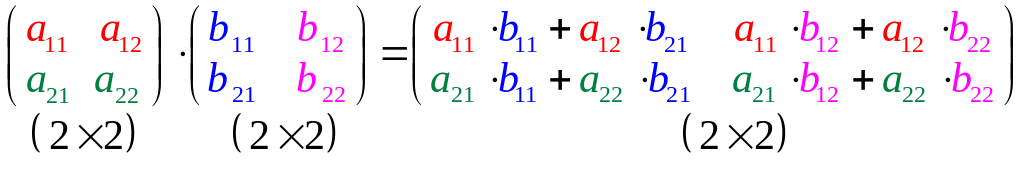
 ычисление
определителей
ычисление
определителей



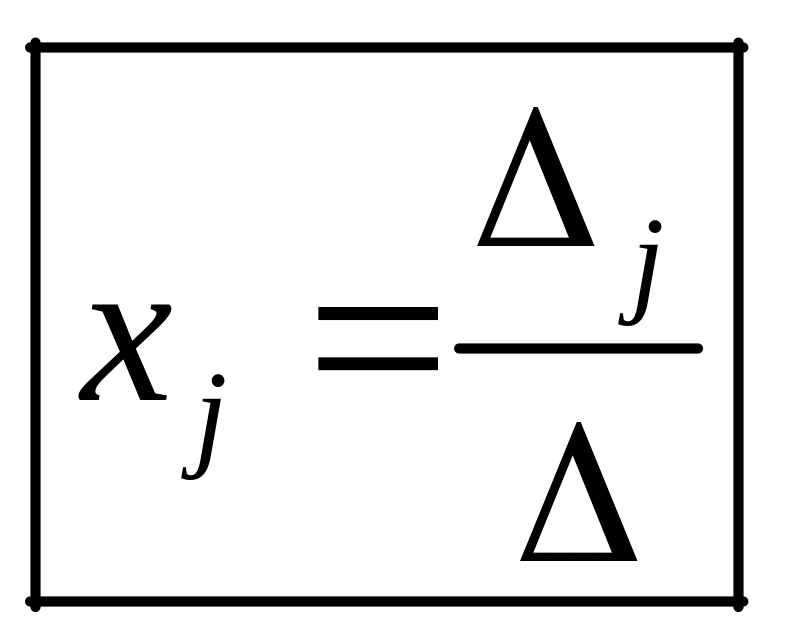
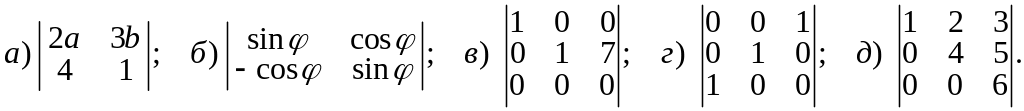

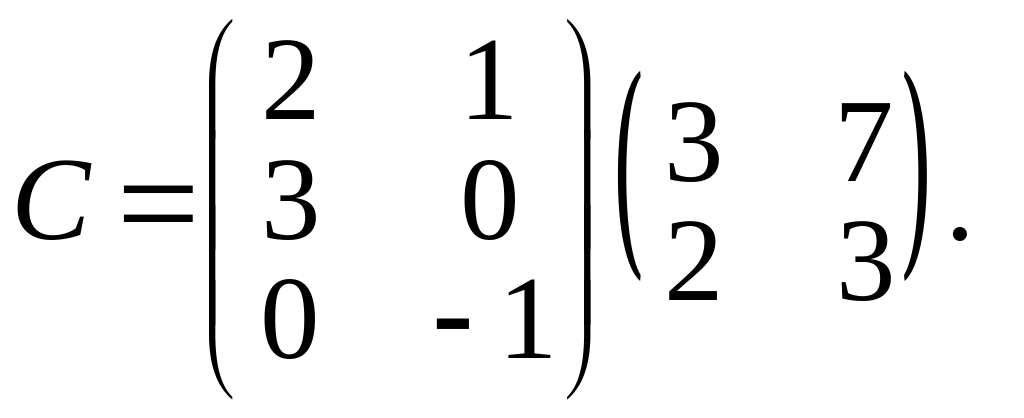
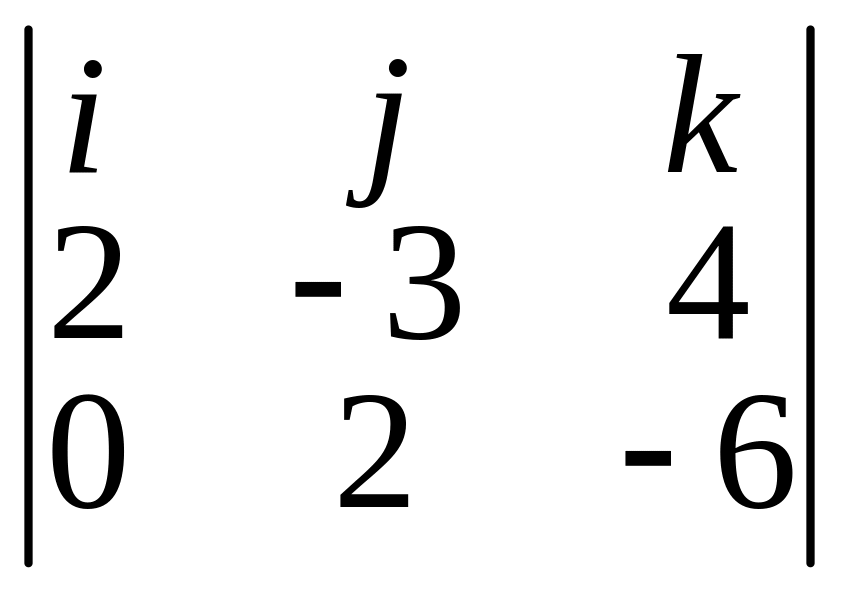 .
.



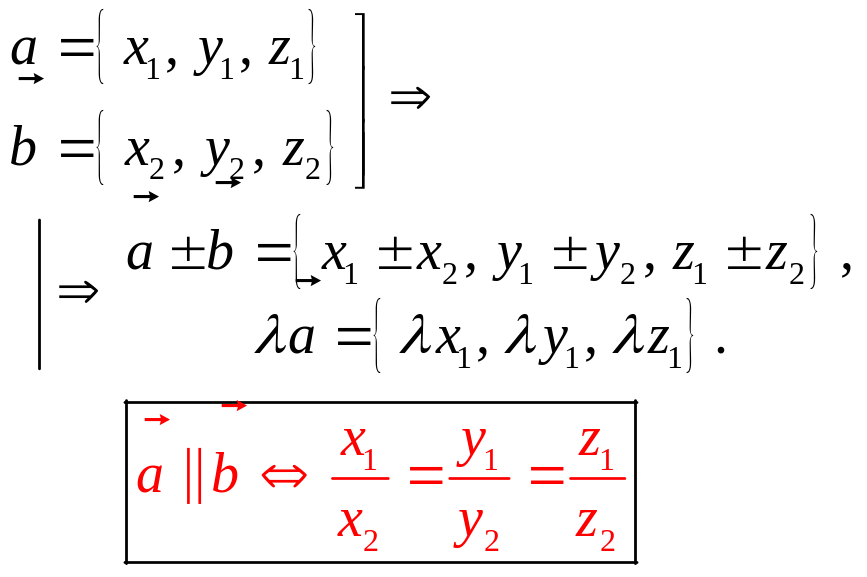


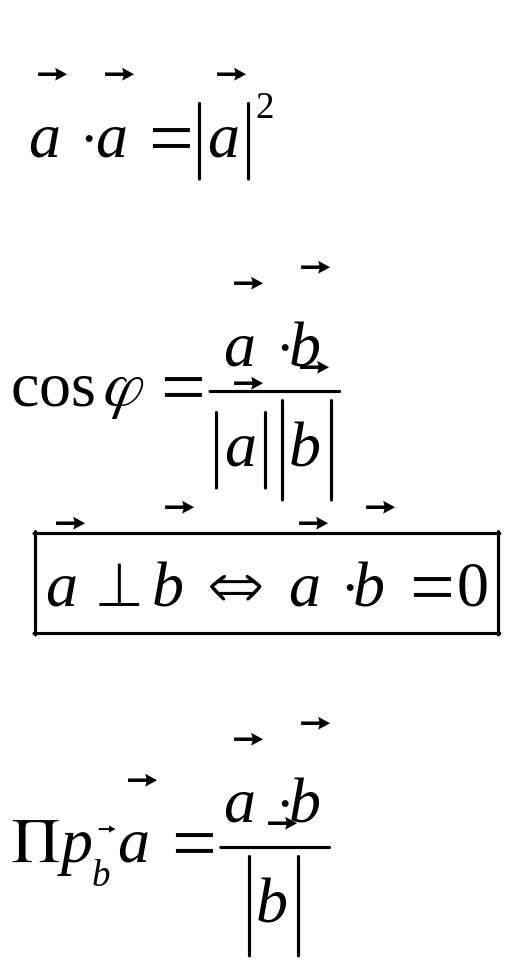
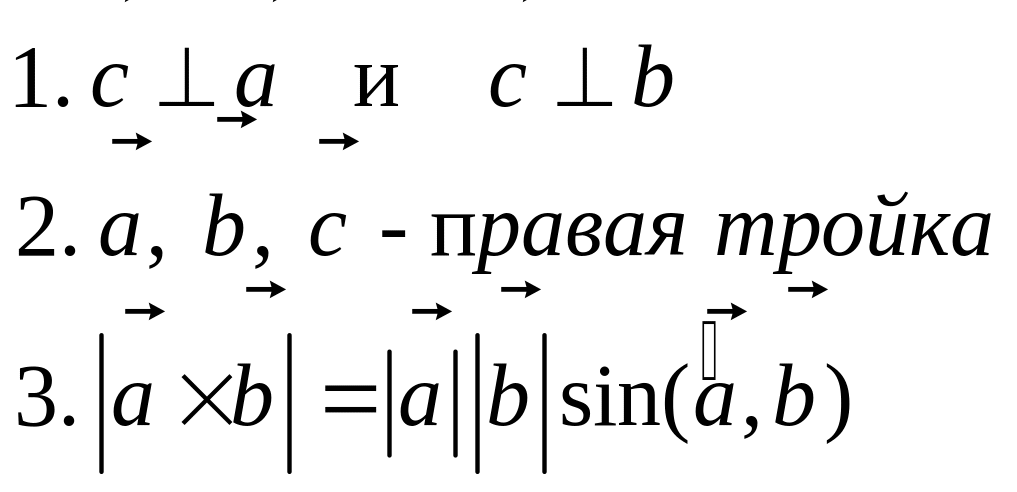 .
.

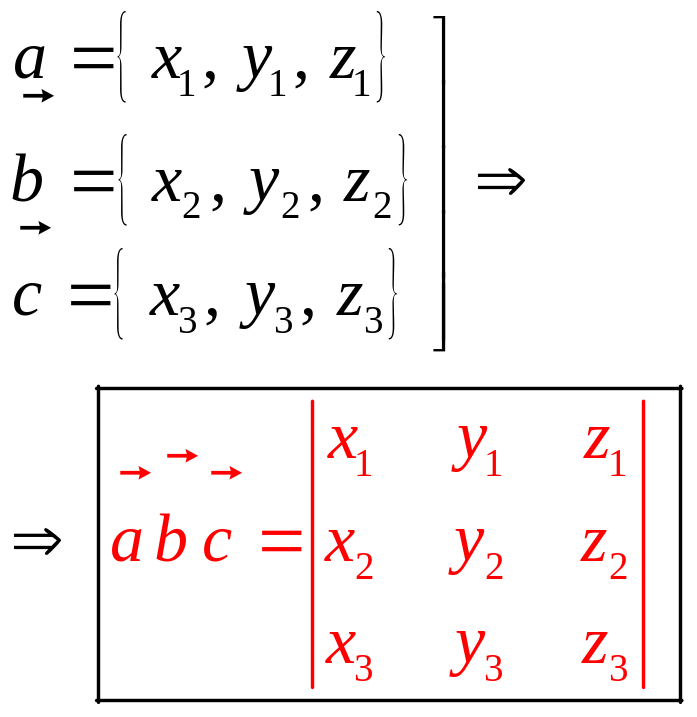

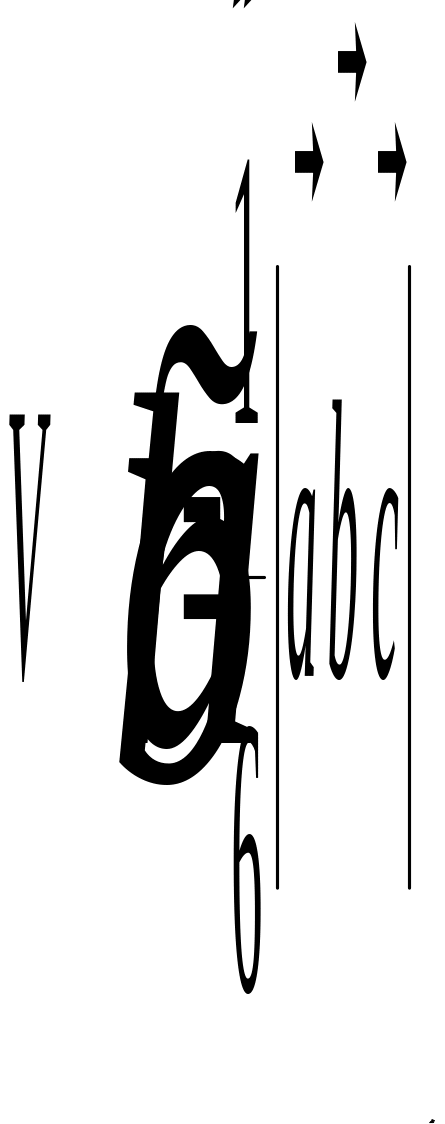



 )
)
 )
)
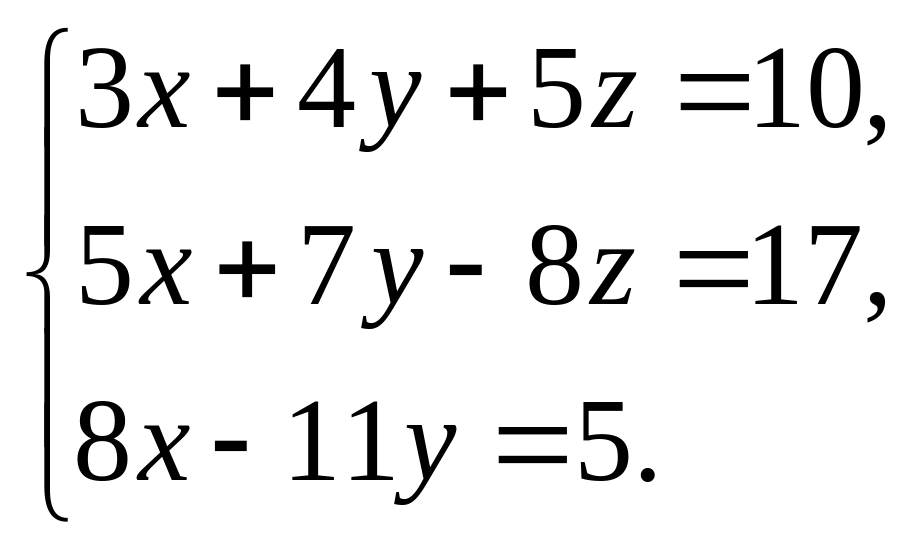
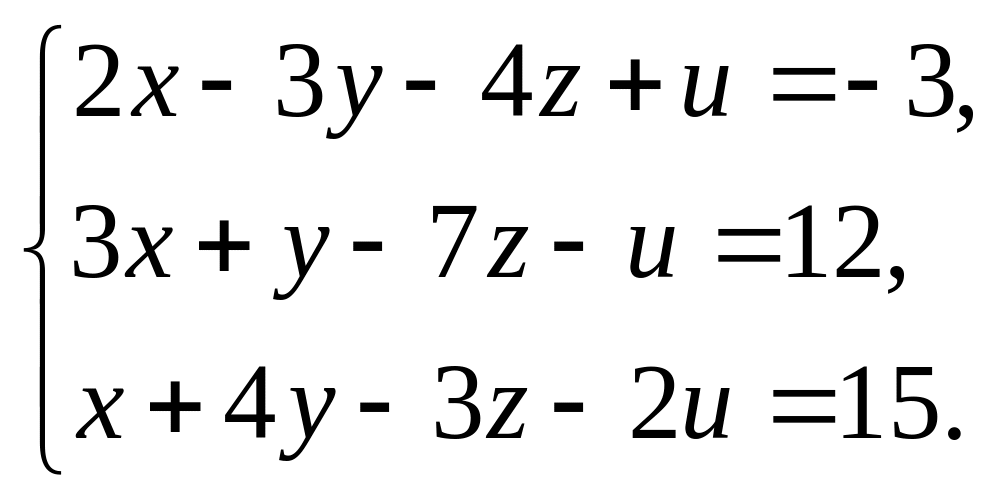
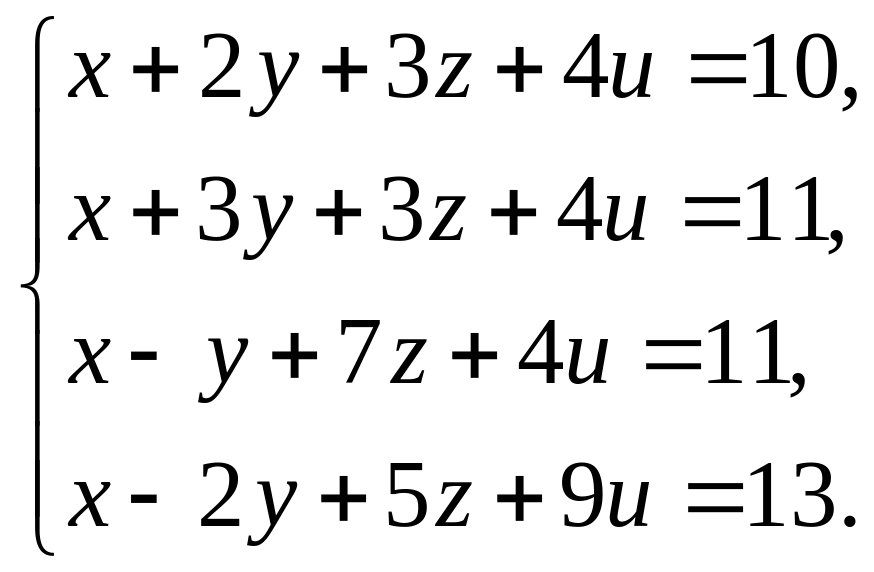





 .
.