
- •1. Общие теоретические сведения
- •2. Блок-схемы алгоритмов
- •Основные блоки блок - схемы
- •3 . Линейные структуры
- •4. Структуры ветвления
- •5. Алгоритмы циклической структуры
- •Протокол возведения числа a в степень n
- •Протокол вычисления суммы четных натуральных чисел
- •6. Алгоритмы со структурами вложенных циклов
- •Массивы линейные
- •Прямоугольные таблицы
- •Символьные переменные
3 . Линейные структуры
Линейная структура – является основной. Она означает, что действия выполняются друг за другом (рис. 2).
П
Рис.2.
Линейная структура
Присваивание переменной какого-либо значения или присваивание одной переменной значения другой переменной является наиболее часто выполняемым действием в программе, написанной на любом языке программирования. В языке программирования присваивание является операцией и обозначается как «:=». Это означает, что при выполнении этой операции происходит не только присваивание значения определенной переменной, но и возвращается некоторое значение. Оператор присваивания имеет вид А : = В. Сначала вычисляется выражение, представленное в правой части, причем все переменные, используемые в правой части, к моменту вычисления должны быть определены. Полученное значение присваивается имени, записанному в левой части. Например, оператор присваивания S := S + Аi выполняется следующим образом: к имеющемуся значению переменной S для заданного номера i элемента последовательности {Ai} вычисляется сумма S + Аi, полученный результат снова записывается в ячейку с именем S. Таким образом, происходит накапливание суммы. Аналогично оператор присваивания Р := Р * Аi осуществляет накапливание произведения. Однако в блок-схемах разрешается использовать знак «=».
Рассмотрим примеры линейных процессов.
Пример 1. По известным катетам прямоугольного треугольника определить радиусы вписанной и описанной окружностей, их площади, а также площадь данного треугольника. Реализовать алгоритм в виде блок-схемы.
Решение.
Расчетные
формулы данной задачи имеют следующий
вид. Пусть a,
b - катеты
прямоугольного треугольника, тогда
гипотенуза
![]() ,
радиус описанной окружности
,
радиус описанной окружности
![]() ,
радиус вписанной окружности
,
радиус вписанной окружности
![]() ,
площади вписанной
и описанной окружностей соответственно
,
площади вписанной
и описанной окружностей соответственно
![]() и
и
![]() ,
площадь данного треугольника
,
площадь данного треугольника
![]() .
Последовательность действий (алгоритм)
представим в виде блок-схемы.
.
Последовательность действий (алгоритм)
представим в виде блок-схемы.


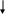




Н



Рис. 3. Блок-схема линейного процесса (задача 1)
Рис.
3. - Блок-схема линейного процесса (задача
1)
Пример 2.
На судно производится погрузка контейнеров. Каждый контейнер имеет длину 3м., ширину 5м. и высоту 7м. Вес каждого контейнера 20 тонн. Сколько контейнеров можно погрузить в трюм размером 50*30*10 и каков общий вес груза?
Решение.
Сначала построим математическую модель поставленной задачи и разработаем последовательность действий (алгоритм). Итак, вычислим объем, занимаемый каждым контейнером: V = a·b·c. Далее, определим, какое максимальное количество контейнеров можно разместить по длине трюма (К1), по ширине (К2) и в высоту (К3). (Замечание: поскольку мы описываем линейный процесс, вопрос оптимизации размещения по длине и ширине не рассматривается!). Теперь подсчитаем общее количество погружаемых контейнеров и, наконец, общий вес груза.
Представим «словесный» алгоритм в виде блок-схемы. Чтобы можно было использовать этот алгоритм при любых размерностях контейнеров и трюма, введем обозначения: a – длина контейнера, b – ширина, c – высота, А – длина трюма, В – его ширина, С - высота, Р - вес одного контейнера.
Обратите внимание на то, что в блоках присваивания К1=целое(К1), К2=целое(К2), К3=целое(К3) в левой и правой части используется одно и то же имя переменной. Это означает, что сначала вычисляется оператор, стоящий в правой части, а полученное значение вносится в ячейку с именем левой части, т.е. изменяется содержимое ячейки.






K1
= целое(К1)
Р
V
= a*b*c
K2
= целое(К2)
K1
= A : a
K3
= целое(К3)
K2
= B : b
K
= К1*К2*К3
K3
= C : c
Робщ
= Р*К


Рис.
4. - Блок-схема линейного процесса
(задача
2)
