II. Исследование деформированного и напряженного состояния в точке абсолютно упругого тела

Одной из важных моделей сплошной среды является абсолютно-упругое тело Гука, т.е. среда, которая полностью восстанавливает свою форму после снятия внешних нагрузок. Под действием вне­шних сил такое тело деформируется и в нем возникает внутреннее напряжение. Для реальных тел при больших внешних нагрузках возникают такие внутренние напряжения и, соответственно, дефор­мации, при которых начинается разрушение материала. Предель-ные напряжения или допустимые напряжения для различных ма­териалов задаются в справочниках. Поэтому при исследовании ме­ханических характеристик упругих тел под воздействием внешних нагрузок важно уметь определять величины максимальных напря­жений и деформаций.

2.1. Постановка задачи

Для абсолютно упругого тела заданы (см. таблицу 2.1):.

1 .Упругие постоянные материала — модуль упругости Е (Н/м²) и коэффициент Пуассона V.

2.Поле перемещений для любой точки U(x,y,z), V(x,y,z), W(x,y,z) (миллиметры).

3. Точка М, положение которой задано единичным вектором

где I, т, п — направляющие косинусы вектора ОМ или, поскольку

\ОМ\ = 1, координаты точки М.

Необходимо определить деформационное и напряженное состо­яние материала в точке М и графически изобразить деформации и вектор полного напряжения по наклонной площадке. Данные взять из таблицы 2.2.

2.2. Исследование деформированного состояния в точке абсолютного упругого тела

Под действием внешней нагрузки абсолютно упругое тело де­формируется, при этом частицы сплошной среды тела перемеща­ются относительно неподвижной среды координат. Поле переме­щений частиц определяется векторной функцией

где U, V, W— функции проекции вектора перемещений S на оси Ox, Оу и Оz.

Согласно теореме Гельмгольца частицы сплошной среды в об­щем случае совершают поступательное, вращательное и деформа­ционное движения.

Деформационное движение определяется тензором деформаций:

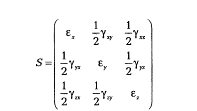
где £_x,E_y,e_z —относительные удлинения (линейные деформации)

вдоль осей Ох, Оуи Oz соответственно; у^ = у у/, У„ =У„; Ууг = Yzy — углы сдвига (угловые деформации) в координатных плоскостях хОу, zOx, yOz, соответственно.

Компоненты тензора деформаций S выражаются через проек­ции векторной функции перемещений S с помощью формул Коши:

Относительное удлинение е_х вдоль какого-либо направления, за-

даваемого единичным вектором у = li -t-m/ + nA в окрестности точ-

ки M(x₀,y₀,z₀) можно определить с помощью компонентов тензора деформаций 5 следующим образом:

Чтобы получить полную картину деформации в точке M(l,m,n), необходимо:

1. Вычислить компоненты тензора деформаций. Для этого в ре­зультаты вычислений по формулам (2.3) необходимо подставить вместо текущих координат числовые значения х=1, у=т, z—n.

2. Записать тензор деформаций в точке М в виде числовой мат­рицы.

3. Рассчитать относительное удлинение е_й/ч по формуле (2.4)

4. Графически изобразить схематично деформацию единичного куба в виде рисунков 3-х проекций куба на плоскости хОу, zOx, yOz с указанием полученных в результате расчетов знаков деформаций, как указано в качестве примера на рис. 2.1.

Рис. 2.1

Задача №4(3.1)

M(1,-1,2)

1.-уменьшение по оси ох

-удлинение по оси оу

-уменьшение по оси оz

2.-тупой угол

-острый угол

-тупой угол M

-удлинение вектора n.