
- •Краткая теория
- •Лабораторная работа № 103 Определение моментов инерции тел на приборе Обербека
- •Теоретическая часть
- •Порядок выполнения работы
- •Контрольные вопросы
- •Порядок выполнения работы
- •Контрольные вопросы
- •Описание метода и экспериментальной установки для определения ускорения свободного падения
- •Порядок выполнения работы
- •Контрольные вопросы
- •Описание экспериментальной установки
- •Порядок выполнения лабораторной работы
- •Контрольные вопросы
- •Обработка результатов измерений по методу Стьюдента
- •Рекомендуемая литература
- •Содержание
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра «Физика»
ДИНАМИКА
ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Лабораторный практикум по физике
№ 103, 104, 105, 106
Ростов-на-Дону
2017
УДК 530.1
Составители: И.Н. Егоров,
С.И. Егорова,
Т.П. Жданова,
В.С. Ковалева,
В.С. Кунаков,
Г.Ф. Лемешко,
О.А. Лещева,
О.М. Холодова
Динамика вращательного движения: лабораторный практикум по физике ; Донской гос. техн. ун-т. – Ростов-на-Дону : ДГТУ, 2017. – 28 с.
Практикум содержит методические указания к четырем лабораторным работам по теме «Динамика вращательного движения». В каждой работе даны краткое описание рабочей установки и методика выполнения работы.
Предназначен для студентов инженерных специальностей всех форм обучения, изучающих физику (раздел «Механика и молекулярная физика»).
Печатается по решению методической комиссии факультета «Автоматизация, мехатроника и управление»
Научный редактор
профессор В.С. Кунаков
© ДГТУ, 2017
Краткая теория
Моментом инерции материальной точки называется скалярная величина, равная произведению массы точки на квадрат расстояния от точки до оси вращения:
 .
.
Моментом инерции твердого тела называется сумма моментов инерции материальных точек, из которых состоит тело:
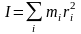 .
.
Момент инерции – это мера инертности при вращательном движении (в этом состоит физический смысл момента инерции).
Теорема Штейнера
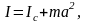
где
 – момент инерции тела относительно
оси, проходящей через центр масс;
– момент инерции тела относительно
оси, проходящей через центр масс;
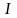 – момент инерции этого тела относительно
параллельной оси, отстоящей от первой
на расстоянии
– момент инерции этого тела относительно
параллельной оси, отстоящей от первой
на расстоянии
 ;
;
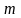 – масса тела.
– масса тела.
Моментом
силы относительно неподвижной точки
называется
векторная физическая величина,
определяемая векторным произведением
радиус-вектора
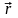 ,
проведенного из данной точки в точку
приложения силы, на силу
,
проведенного из данной точки в точку
приложения силы, на силу
 :
:
 .
.
Модуль момента силы относительно неподвижной оси:
 ,
,
где
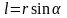 –
плечо силы (кратчайшее расстояние между
линией действия силы и осью вращения);
–
плечо силы (кратчайшее расстояние между
линией действия силы и осью вращения);
 – угол между направлениями силы и
радиуса-вектора. Направление момента
силы совпадает с осью, относительно
которой происходит вращение, и может
быть определено по правилу буравчика.
– угол между направлениями силы и
радиуса-вектора. Направление момента
силы совпадает с осью, относительно
которой происходит вращение, и может
быть определено по правилу буравчика.
Работа при вращении тела
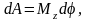
где
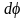 –
угол поворота тела;
–
угол поворота тела;
 – момент силы относительно оси
– момент силы относительно оси
 .
.
Момент импульса (момент количества движения) твердого тела относительно оси вращения :

где
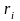 – расстояние от оси
до отдельной частицы тела;
– расстояние от оси
до отдельной частицы тела;
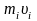 – импульс этой частицы;
– импульс этой частицы;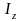 –
момент инерции тела относительно оси
;
–
момент инерции тела относительно оси
;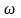 – его угловая скорость.
– его угловая скорость.
Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси :
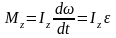 или
или
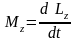 ,
,
где
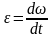 – угловое ускорение;
– момент инерции тела относительно
оси
;
– угловое ускорение;
– момент инерции тела относительно
оси
;
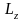 –
момент импульса тела относительно оси
.
–
момент импульса тела относительно оси
.
Кинетическая энергия тела, вращающегося вокруг неподвижной оси ,

где – момент инерции тела относительно оси ; – его угловая скорость.
Кинетическая энергия тела, катящегося по плоскости без скольжения,
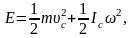
где
– масса тела;
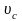 – скорость центра масс тела;
– момент инерции тела относительно
оси, проходящей через его центр масс;
– угловая скорость тела.
– скорость центра масс тела;
– момент инерции тела относительно
оси, проходящей через его центр масс;
– угловая скорость тела.
Лабораторная работа № 103 Определение моментов инерции тел на приборе Обербека
Цель работы: определение момента инерции тела на приборе Обербека.
Оборудование: экспериментальная установка, секундомер.
Теоретическая часть
Маятник
Обербека (рис. 1) состоит из шкива радиуса
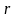 и четырёх крестообразно расположенных
тонких стержней, укреплённых на одной
горизонтальной оси. По стержням можно
перемещать и закреплять в нужном
положении четыре дополнительных груза
одинаковой массы
и четырёх крестообразно расположенных
тонких стержней, укреплённых на одной
горизонтальной оси. По стержням можно
перемещать и закреплять в нужном
положении четыре дополнительных груза
одинаковой массы
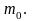 Маятник приводится во вращательное
движение при помощи груза массы
,
прикреплённого к шнуру, намотанному на
шкив.
Маятник приводится во вращательное
движение при помощи груза массы
,
прикреплённого к шнуру, намотанному на
шкив.

Рис. 1
При
разматывании нити груз
опускается, пройдя расстояние
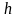 ,
измеряемое по шкале. Определив время
падения, можно найти ускорение, с которым
падает груз:
,
измеряемое по шкале. Определив время
падения, можно найти ускорение, с которым
падает груз:
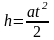
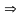
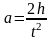 .
(1)
.
(1)
Запишем второй закон Ньютона для груза в проекции на направление движения:

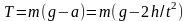 ,
(2)
,
(2)
где
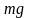 –
сила тяжести;
–
сила тяжести;
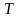 –
сила натяжения нити.
–
сила натяжения нити.
На
шкив действует сила
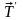 ,
под действием которой он совершает
вращение с угловым ускорением
,
под действием которой он совершает
вращение с угловым ускорением
 .
(3)
.
(3)
Поскольку
по третьему закону Ньютона
 ,
можно записать, что момент силы, вращающий
шкив, равен
,
можно записать, что момент силы, вращающий
шкив, равен
 .
(4)
.
(4)
Запишем основное уравнение динамики вращательного движения

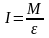 ,
(5)
,
(5)
где - момент инерции вращающейся системы тел маятника Обербека.
Подставляя
в уравнение (5)
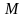 из
(4) и
из
(4) и
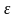 из (3) , получаем
из (3) , получаем
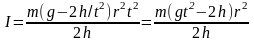 .
.
Учитывая,
что радиус шкива равен половине его
диаметра, т.е.
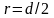 ,
получаем окончательную формулу для
вычисления момента инерции системы
,
получаем окончательную формулу для
вычисления момента инерции системы
 .
(6)
.
(6)
Для
нахождения момента инерции
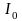 грузиков
грузиков
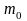 необходимо найти момент инерции
нагруженной системы
необходимо найти момент инерции
нагруженной системы
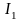 и момент инерции ненагруженной системы
и момент инерции ненагруженной системы
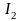 :
:
= - . (7)
