Практичне заняття

Розв’язання задач на розрахунок обертального руху твердого тіла

Мета: Поглибити поняття про види обертального руху. Розвивати у студентів логіку мислення під час розв’язання задач різного типу.

Студенти повинні вміти: визначати основні характеристики обертального руху твердого тіла, використовувати здобуті знання для розв’язування практичних задач.

Основі теоретичні положення Динамічні характеристики обертального руху абсолютно твердого тіла (атт)

Момент сили , або обертальним моментом відносно точки обертання O, називається векторний добуток радіуса-вектора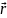 , проведеного з точки О в точку прикладання сили, а цю силу :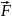

.

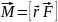Визначення моменту сили дано так, щоб кутове прискорення і кутова швидкість, які виникають в наслідок дії моменту сили, збігалися за напрямком з цим моментом. Тобто вектор спрямований перпендикулярно до площини розташування векторів 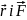згідно з правилом правого гвинта (рис. 1а)

Модуль моменту сили дорівнює:

Де 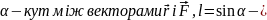перпендикуляр, проведений з точки O на лінію дії сили , який називається плечем сили.

Одиницею вимірювання моменту сили є ньютон-метр (Н∙м).

Якщо на тіло діє кілька сил, можна знайти суму моментів цих сил відносно точки обертання 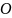. Ця сума називається головним моментом зовнішніх сил відносно обертання О:

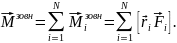
Моментом сили відносно осі обертання zназивають проекцію вектора відносно точки обертання О на цю вісь за умови , що вісь z проходить через цю точку О (рис. 1б)

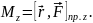
z

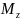
α

O

a

б

Якщо вектор зберігається за напрямком я віссю z, то його проекція дорівнює модулю вектора :

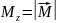
Нехай на тіло діють дві сили, рівні між собою за модулем, а спрямованні протилежно вздовж паралельних прямих. Такі сили називаються парою сил (рис. 2.)

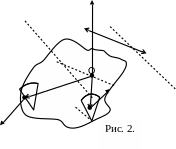
Момент пари сил відносно точки О

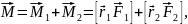
а його модуль

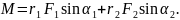
Оскільки

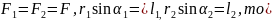
де 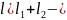плече пари, тобто найкоротша відстань між прямими, вздовж яких діють сили. Здобутий вираз не залежить від розташування точки О.

У загальному випадку, щоб тіло, на яке діють різні зовнішні сили, не оберталось, тобто перебувало в рівновазі, сумарний момент цих сил має дорівнювати нулю:

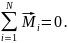
2. Момент інерції

Уявно розіб’ємо АТТ на малі елементи об’ємом 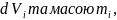які можна вважати матеріальними точками (тобто подамо АТТ, як систему матеріальних точок з масою .

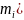Моментом інерції матеріальних точок Iвідносно деякої осі zназивається добуток маси матеріальної точки 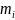на квадрат її відстані від цієї осі (рис. 3).

.

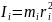Момент інерції всього тіла відносно деякої осі zдорівнює сумі моментів інерції всіх його точок відносно цієї осі:

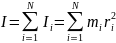
Ця величина скалярна, одиниця вимірювання в

системіСІ .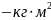

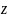
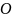
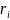
Рис. 3.

Момент інерції має кожне тіло незалежно від свого руху. Подібно до того, яку тіло має незалежну від свого стану руху чи спокою, воно має і момент інерції будь-якої осі незалежно від того, обертається воно навколо своєї осі чи ні.

Як впливає з означення , момент інерції залежить не тільки від маси тіла, але й від того, як ця маса розподілена по об’єму тіла. Враховуючи, що

та переходячи від додавання до інтегрування, перепишемо вираз

де, ρ 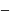густина речовини у вибраному об’ємі 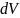; 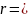відстань цього об'єму від осі, відносно якої обчислюється момент інерції. Знаходження цього інтеграла в загальному випадку є досить складним.

Задача значно спрощується, якщо розглядати однорідні тіла правильної геометричної форми.

Наведемо вираз для моментів інерції деяких тіл:

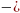
момент інерції диска (циліндра) з радіусом Rвідносно осі симетрії:

момент інерції обруча (тонко стійного порожнинного циліндра) з радіусом R відносно осі симетрії:

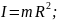
момент інерції соціальної кулі

м

омент інерції куліз радіусом Rвідносно осі, що проходить через центр кулі:

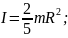
момент інерції однорідного стрижня довжиною lвідносно осі, що проходить через його середину перпендикулярно до l;

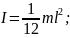
те саме відносно осі, що проходить через кінець стрижня:

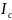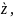Як бачимо, момент інерції тіла залежить не тільки від маси, форми і розмірів тіла, а й від розташування тіла відносно осі.Можна обчислити момент інерції тіла відносно будь-якої осі. Для цього зручно використовувати теорему Штейнера: момент інерції тіла I відносно довільної осі z дорівнює сумі моменту інерції тіла відносно осі що проходить через його центр мас паралельно даній осі z, і добутку маси тіла mна квадрат відстані dміж осями (рис. 4):

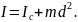
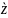
C

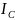
Рис. 4