86

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «КУЗБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ Т.Ф. ГОРБАЧЕВА»

Т.В. Богданова

	НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ, ИНЖЕНЕРНАЯ И КОМПЬЮТЕРНАЯ ГРАФИКА Учебное пособие
		Рекомендовано учебно-методической комиссией направления подготовки 140100.62 «Теплоэнергетика и теплотехника» в качестве электронного учебного пособия

Кемерово 2013

Рецензенты:

М. Т. Кобылянский, профессор ФИО, должность	кафедры		Начертательная геометрия и графика наименование кафедры
А. Р. Богомолов, председатель ФИО, член УМК или председатель		УМК по направлению		140100.62 – «Теплоэнергетика и теплотехника»
Татьяна Витальевна Богданова. Начертательная геометрия, инженерная и компьютерная графика: учебное пособие [Электронный ресурс] : для студентов направления подготовки 140100.62 «Теплоэнергетика и теплотехника» профиля подготовки «Промышленная теплоэнергетика» / Т. В. Богданова – Электрон. дан. – Кемерово : КузГТУ, 2013. – 1 электрон. опт. диск (CD-RW) ; зв. ; цв. ; 12 см. – Систем. требования : Pentium IV ; ОЗУ 8 Мб ; Windows 95 ; (CD-ROM-дисковод) ; мышь. - Загл. с экрана.

В работе в краткой форме представлен теоретический материал по указанной дисциплине. Темы приводятся в порядке возрастания сложности. Основные вопросы изложены по пунктам, сопровождаются определениями ключевых понятий и алгоритмами решения. Все темы содержат графические примеры с различными вариантами расположения геометрических образов. Методическая разработка может быть полезна для самостоятельной работы студентов и закрепления прочитанного на лекции материала.

 КузГТУ

 Богданова Т. В.

Лекция 1

ВВедение

Начертательная геометрия – наука, изучающая закономерности изображения на плоскости пространственных объектов и решения пространственных задач проекционно-графическими методами. Начертательную геометрию из других ветвей геометрии выделяет то обстоятельство, что она для решения общегеометрических задач использует графический путь, при котором геометрические свойства фигур изучаются непосредственно по чертежу.

Проекционное изображение, по которому можно восстановить объект, является чертежом. Чертеж отличается от других изображений тем, что он построен по правилам начертательной геометрии, а также согласно действующим стандартам ЕСКД, и в соответствии с этими правилами позволяет определить геометрические свойства изображаемого объекта. Таким образом, чертеж является носителем геометрических свойств изображаемого объекта.

Проекционный метод построения изображений является основным методом начертательной геометрии. Этим своим, единственно ей присущим, методом начертательная геометрия отличается от всех остальных ветвей геометрии.

Цель и метод начертательной геометрии определяют ее задачи (содержание):

изучение способов построения изображений как существующих, так и вновь создаваемых предметов;

изучение способов определения при помощи чертежа формы и размеров предмета (чтение чертежа);

изучение графических способов решения геометрических задач на плоскости;

приложение способов начертательной геометрии к исследованию практических и теоретических задач науки и техники.

Изучение начертательной геометрии развивает геометрическую логику и пространственное представление, способность мыслить пространственными образами. Эта способность необходима любому инженеру, поскольку инженерная деятельность связана с разработкой и проектированием пространственных объектов и их плоскостным изображением. Таким образом, начертательная геометрия является одним из существенных элементов профессиональной квалификации инженера.

Принятые обозначения:

A, B, C – точки;

a, b, c – линии;

Γ, Π, Ρ, Σ, Τ, Φ, Ψ – поверхности (плоскости);

, β, γ, ,  – углы;

 или  – знаки принадлежности, включения: С  d (точка С принадлежит линии d), Ψ  b (плоскость Ψ проходит через прямую b);

∩ – знак пересечения;

 – знак результата операции: a ∩ b = К (линия a пересекает линию b в точке К);

 – знак совпадения: а  b (линия а совпадает с линией b);

|| – знак параллельности;

– знак скрещивания;

 – знак перпендикулярности;

– прямой угол ( 90^о);

 – знак логического следствия (например, запись а || b  а₁ || b₁ обозначает, что если прямая а параллельна прямой b, то проекции этих прямых а₁ и b₁ соответственно параллельны).

Из истории начертательной геометрии

 С древних времён человек пытался сохранить образ увиденного. Так появилась наскальная живопись. Затем человек стал украшать рисунками стены своего жилища, посуду, орудия труда и другие предметы быта. Цивилизация развивалась, и перед человеком стали возникать все более серьёзные технические задачи: составление схем и карт местности, изображение военных сооружений и жилых домов, мостов, орудий и предметов труда. Различные сферы человеческой деятельности, развитие производства требовали выработки неких общих правил и стандартов представления пространственной информации на плоскости.

Ещё греческие и римские учёные, начав с изучения перспективы, пытались выработать некоторые правила представления имеющейся информации. В эпоху Возрождения начинается расцвет архитектуры, скульптуры, живописи, что приводит к разработке теоретических основ перспективы. Основателем теоретической перспективы был итальянский учёный Л. Альберти (1404-1472). Гениальный итальянский учёный и художник Леонардо да Винчи (1452-1519) дополнил линейную перспективу учением "Об уменьшении цветов и отчётливости очертаний".

Начертательная геометрия как наука была создана в конце XVIII века великим французским геометром и инженером Гаспаром Монжем (1746 – 1818).

Первые идеи об ортогональном проецировании пространственных фигур на плоскость высказывались еще задолго до Монжа в XVI веке немецким математиком и художником Альбрехтом Дюрером (1471 –1528), который разработал метод ортогонального изображения конических сечений и некоторых пространственных кривых.

В 1637 г. французский геометр и философ Рене Декарт (1596 – 1650) создал метод координат и заложил основы аналитической геометрии, а его соотечественник, инженер и математик Жирар Дезаг (1593 – 1662), использовал этот метод координат для построения перспективных проекций и обосновал теорию аксонометрических проекций.

В XVII веке в России успешно развивались технические чертежи, выполненные в виде планов и профилей в масштабе. Здесь в первую очередь следует назвать чертежи выдающегося русского механика и изобретателя И. П. Кулибина (1735 – 1818). В его проекте деревянного арочного моста впервые были использованы ортогональные проекции (1773).

Большой вклад в развитие ортогональных проекций внес французский инженер А. Фрезье (1682 –1773), который впервые рассмотрел проецирование объекта на две плоскости – горизонтальную и фронтальную.

Величайшей заслугой Г. Монжа явилось обобщение всех научных трудов его предшественников, всей теории о методах изображения пространственных фигур и создание единой математической науки об ортогональном проецировании – начертательной геометрии. Влюбленный в свое детище - начертательную геометрию, Монж писал: "Очарование, сопровождающее науку, может победить свойственное людям отвращение к напряжению ума и заставить их находить удовольствие в упражнении своего разума, - что большинству людей представляется утомительным и скучным занятием"

Развитию начертательной геометрии в нашей стране способствовали такие художники, зодчие и учёные как А. Рублёв, Дионисий, В. Баженов, А. Воронихин, И. Ползунов, И. Кулибин и другие. Первым русским профессором начертательной геометрии был Я. А. Севостьянов (1796-1849), который создал оригинальный курс начертательной геометрии. Далее начертательная геометрия развивалась, открывая такие имена, как Н. И. Макаров, В. И. Курдюмов, А. К. Власов, Н. А. Глаголев, Н. Ф. Четверухин и многие другие.

1 Способы проецирования

Операция проецирования заключается в следующем. В пространстве выбираем центр проецирования S и плоскость проекций π₁. Через произвольную точку А пространства проводим проецирующий луч SA до пересечения с плоскостью π и получаем проекцию точки А (рис. 1).

Проекция любой геометрической фигуры есть множество проекций всех ее точек. Направление проецирующих лучей  и положение плоскостей π₁ определяют аппарат проецирования

Рис. 1. Проекция точки А на плоскость проекций π₁

Центральным проецированием называется такое проецирование, при котором все проецирующие лучи исходят из одной точки S – центра проецирования (рис. 2).

Основными и неизменными свойствами (инвариантами) центральных проекций являются следующие:

• проекция точки есть точка;

• проекция прямой – прямая;

• точка, лежащая на прямой, проецируется в точку, лежащую на проекции этой прямой.

Рис. 2. Пример центрального проецирования

Метод обладает большой наглядностью, однако в значительной степени искажает форму и размеры оригинала, так как не сохраняет параллельности прямых и отношения отрезков.

Метод центрального проецирования применяется в основном при построении перспективных проекций в строительстве и архитектуре.

Параллельным проецированием называют такое проецирование, при котором все проецирующие прямые параллельны заданному направлению S (рис. 3).

а б

Рис. 3 Пример параллельного проецирования: а – косоугольное проецирование; б – прямоугольное проецирование.

Параллельное проецирование представляет собой частный случай центрального проецирования, когда точка S находится на бесконечно большом расстоянии от плоскости проекций π₁ и, следовательно, проецирующие лучи становятся параллельными друг другу.

Если направление проецирования S перпендикулярно плоскости π_1, то проецирование называют прямоугольным параллельным проецированием (рис. 3б). Если угол наклона направления проецирования S к плоскости π_1, отличен от прямого, то проецирование называют косоугольным параллельным проецированием (рис. 3а).

При заданном аппарате проецирования каждой точке пространства соответствует одна и только одна точка на плоскости проекций.

Одна проекция точки не определяет положения этой точки в пространстве. Действительно, проекции А₁ может соответствовать бесчисленное множество точек А^’, А^’’, …, расположенных на проецирующем луче SA  (рис. 4).

Рис. 4 Пример расположения множества точек на проецирующей прямой

Для определения положения точки в пространстве при любом аппарате проецирования необходимо иметь две ее проекции, полученных при двух различных направлениях проецирования (или при двух различных центрах проецирования

Параллельные и прямоугольные взаимноперпендикулярные проекции двух и более плоскостей называются ортогональными проекциями.

Свойства параллельных проекций:

1,2,3 свойства подобны свойствам центральных проекций;

• проекции параллельных прямых параллельны между собой;

• отношение отрезков прямой линии равно отношению их проекций.

Параллельное проецирование применяется при построении аксонометрических, ортогональных проекций и проекций с числовыми отметками.

Ортогональные проекции получили наибольшее распространение в технических чертежах, так как они позволяет точно судить о размерах изображаемых объектов.

1.2 Ортогональный чертёж точки

Точка, как математическое понятие не имеет размеров. Очевидно, если объект проецирования является нульмерным образом, то говорить о его проецировании бессмысленно.

В геометрии под точкой целесообразно понимать физический объект, имеющий линейные измерения. Условно за точку будем принимать шарик с бесконечно малым радиусом. При такой трактовке понятия точки можно говорить о ее проекциях.

Способ комплексных проекций основан на том, что предмет (точку) проецируют на несколько взаимноперпендикулярных плоскостей проекций. При использовании трех плоскостей проекций плоскость располагают горизонтально и называют горизонтальной плоскостью проекций. Плоскость располагают вертикально под углом 90° и называют фронтальной плоскостью проекций. Плоскость располагают вертикально под углами 90° к и и называют профильной плоскостью проекций (рис. 5).

А – точка в пространстве:

А₁ – горизонтальная проекция точки А;

А₂ – фронтальная проекция точки А;

А₃ – профильная проекция точки А;

x, y, z – оси проекций;

А _x, А _y, А _z – проекции точки А на соответствующие оси координат.

АА₁ ∩ А₁: АА₂ ∩ А₂; АА₃ ∩ А₃.

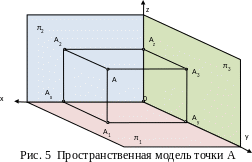
Две проекции точки определяют ее положение в пространстве. Точка А имеет координаты x, y, z. Горизонтальная проекция точки А₁ имеет координаты x, y. Фронтальная проекция точки А₂ имеет координаты x, z. Профильная проекция точки А₃ имеет координаты z, y. Следовательно, набор любых двух проекций будет иметь все три координаты x, y, z.

Расстояние от точки А до плоскостей проекций определяется:

абсциссой х=АА₃= А₁А_у= А₂А_z=0A_x – расстояние до плоскости :

ординатой у= АА₂= А₁А_x= А₃А_z=0A_y – расстояние до плоскости :

аппликатой z= АА₁= А₃А_у= А₂А_x=0A_z – расстояние до плоскости .

При решении задач пользоваться пространственным чертежом неудобно, поэтому от пространственного чертежа переходят к плоскому чертежу, который называют комплексным чертежом или эпюром. Плоскость остаётся неподвижной, плоскость вращается вокруг оси x на 90° до совмещения с плоскостью а плоскость вращается вокруг оси z до совмещения с плоскостью .

Полученное совмещение трех плоскостей проекций (рис. 6) является плоской моделью системы трех пространственных координатных плоскостей.

Для построения плоской модели пространственной геометрической фигуры каждая ее точка проецируется ортогонально на плоскости проекций π₁, π₂ и π₃, которые затем совмещаются в одну плоскость. Полученная таким образом плоская модель пространственной геометрической фигуры называется эпюром Монжа.

Рис. 6 Эпюр точки А

На рис. 6 плоскости проекций π₁ и π₃ совмещены с плоскостью чертежа (с плоскостью проекции π₂), а вместе с ними совмещены с плоскостью чертежа и проекции точки А (А₁, А₂, А₃) и, таким образом, получена плоскостная модель координатных плоскостей проекций и плоскостная модель пространственной точки А – ее эпюр.

Положение проекций точки А на эпюре однозначно определяется ее тремя координатами (рис. 6).

На рис. 5 и рис. 6 также видно, что на эпюре горизонтальная и фронтальная проекции точки лежат на одном перпендикуляре к оси Х, а также фронтальная и профильная проекции – на одном перпендикуляре к оси Z: А₁А₂   Х, А₂А₃   Z.

Линия связи  - это прямая, связывающая пары проекций одной и той же точки, и перпендикулярная оси проекций.

1.3 Метод конкурирующих точек

Метод конкурирующих точек используется в начертательной геометрии для определения взаимной видимости двух геометрических фигур.

Конкурирующими точками называются такие точки пространства, у которых совпадают какие-либо две одноименные проекции.

На рис. 7 показаны конкурирующие точки А и В (совпадают горизонтальные проекции А₁≡В₁) и C и D (совпадают фронтальные проекции С₂≡D₂).

Рис.7 Конкурирующие точки

Метод конкурирующих точек заключается в определении взаимной видимости точек (фигур) по их несовпадающим проекциям. Точка В находится выше точки А относительно плоскости π₁ (Z_B>Z_A), поэтому на плоскости π₁ видна точка В, которая закрывает точку А (считается, что наблюдатель смотрит на плоскости проекций из бесконечности и направление луча зрения параллельно проецирующему лучу S).

На плоскости π₂ видна точка D, так как она находится ближе к наблюдателю (дальше от плоскости π₂, Y_D>Y_C) и закрывает невидимую точку С.

Точки, расположенные дальше от плоскостей проекций перекрывают точки расположенные ближе к плоскости проекций.

Лекция 2.