
Лабораторная работа № 5 измерение ускорения свободного падения
Цель работы ‑ измерение ускорения свободного падения на машине Атвуда.
Приборы и принадлежности
Машина Атвуда, линейка, 4 груза с известной массой.
1. Введение
Рассмотрим движение системы, состоящих из двух грузов массой m и m= m + m1 . Эти грузы подвешены на нерастяжимой нити, которая перекинута через блок (рис1).
Е сли
предположить, что блок невесомый, то
его вращательное движение не учитывается,
и натяжение нити будут одинаковы и
справа, и слева. Условие нерастяжимости
нити приводит к тому, что грузы движутся
с одинаковым ускорением. Величину
ускорения можно найти, написав уравнения
движения каждого груза в отдельности.
На каждый груз будет действовать две
силы – сила тяжести P
= mg
и сила натяжения нити T.
Так как эти силы направлены по вертикали,
то достаточно рассмотреть движение
вдоль вертикальной оси. Проекции сил и
ускорения на эту ось равны соответствующим
модулям, а направления их можно учесть
знаками. Силы будем считать положительными,
если их направление совпадает с
направлением приобретаемого телом
результирующего ускорения. Положим,
тело движется в сторону груза с
перегрузкой. На основании второго
закона Ньютона можно записать для
первого груза:
сли
предположить, что блок невесомый, то
его вращательное движение не учитывается,
и натяжение нити будут одинаковы и
справа, и слева. Условие нерастяжимости
нити приводит к тому, что грузы движутся
с одинаковым ускорением. Величину
ускорения можно найти, написав уравнения
движения каждого груза в отдельности.
На каждый груз будет действовать две
силы – сила тяжести P
= mg
и сила натяжения нити T.
Так как эти силы направлены по вертикали,
то достаточно рассмотреть движение
вдоль вертикальной оси. Проекции сил и
ускорения на эту ось равны соответствующим
модулям, а направления их можно учесть
знаками. Силы будем считать положительными,
если их направление совпадает с
направлением приобретаемого телом
результирующего ускорения. Положим,
тело движется в сторону груза с
перегрузкой. На основании второго
закона Ньютона можно записать для
первого груза:
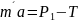
или
 (1)
(1)
для второго груза:
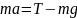 (2)
(2)
Решение этих уравнений даёт величину ускорения а и величину натяжения
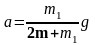 (3)
(3)
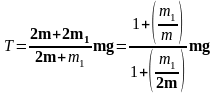 (4)
(4)
Если а > 0, то есть система перемещается в сторону груза с перегрузком и груз m поднимается, то сила натяжения Т больше mg.
Для более точного определения ускорения системы, необходимо учитывать массу блока m0. Кроме того, положим, что нить движется на блоке без скольжения. В этом случае силы натяжения нити по обе стороны блока будут различны. Вращение блока возникает в результате действия разности моментов сил натяжения нитей. При равенстве плеч той и другой сил вращения может возникнуть только, если сами силы по величине различны.
Напишем уравнение моментов для вращательного движения блока относительно его оси. Положительным будем считать момент, действующий в направлении вращения (по часовой стрелке):
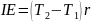 (5)
(5)
где I – момент инерции блока, равный m0 r2; m0 – масса блока; r – радиус блока; Е – угловое ускорение; - коэффициент, зависящий от распределения массы блока.
По-прежнему составим уравнение поступательного движения грузов:
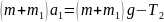 (6)
(6)
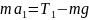 (7)
(7)
Система уравнений (5 – 7) является незамкнутой. Используем условия отсутствия скольжения нити, чтобы получить связь между угловым ускорением вращательного движения блока и линейным ускорением грузов:
 (8)
(8)
Решение приведённой выше системы уравнений даёт ускорение:
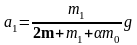 (9)
(9)
И значение сил натяжения нитей Т1 и Т2.
Сила трения ещё уменьшает величину ускорения.
Как видно из приведённых выше формул, система будет двигаться с ускорением, меньшим, чем ускорение свободного падения g. Увеличивая перегрузок m1 , можно увеличить и ускорение системы. Если перегрузок m1 во время движения снять, то в случае малого трения дальнейшее движение системы будет происходить с постоянной скоростью, равной скорости в момент снятия перегрузка. Такого рода блок с перекинутой через него нитью с двумя грузами представляет собой демонстрационный прибор (машина Атвуда), служащий для иллюстрации второго закона Ньютона.
