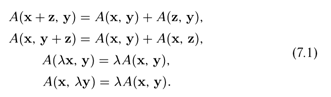21 Вопрос.
Определение квадратичной формы. Преобразование квадратичных форм. Квадратичные формы канонического вида. Единственность симметричной билинейной формы, порождающей квадратичную форму.
Квадратичной формой называется однородный многочлен второй степени от n переменных с действительными коэффициентами
f ()= , где = ,
Симметрическая матрица А = составленная из коэффициентов квадратичной формы, называется матрицей квадратичной формы.
Привести квадратичную форму к каноническому виду - значит представить ее следующим образом:
.
22 Вопрос.
Критерий Сильвестра положительной определенности квадратичной формы. Закон инерции для квадратичных форм. Билинейные формы.
Критерий Сильвестра определяет, является ли симметричная квадратная матрица положительно (отрицательно, неотрицательно) определённой.
Критерий положительной определённости квадратичной формы.
1. «Необходимо.» Имеется положительно определённая квадратичная форма. j-ый диагональный элемент положителен, так как k(x)>0 в том числе и для вектора со всеми нулевыми координатами, кроме j-ой. При приведении матрицы к каноническому виду не будет нужно переставлять строки, и знаки главных миноров матрицы не изменятся. А в каноническом виде диагональные элементы положительны, и миноры положительны; следовательно, (так как их знак не менялся при преобразованиях), у положительно определённой квадратичной формы в любом базисе главные миноры матрицы положительны.
2. «Достаточно.» Имеется положительность миноров. Первый минор определяет знак первого диагонального элемента в каноническом виде. Знак отношения Mi+1/Mi определяет знак i+1-го элемента в диагональном виде. Так получим, что в каноническом виде все элементы на диагонали положительные, то есть квадратичная форма определена положительно.
Для положительной определённости квадратичной формы необходимо и достаточно, чтобы главные миноры её матрицы были положительны. |
Критерий отрицательной определённости квадратичной формы.
Для отрицательной определённости квадратичной формы необходимо и достаточно, чтобы главные миноры чётного порядка её матрицы были положительны, а нечётного порядка — отрицательны. |
Закон инерции квадратичных форм гласит: число положительных, отрицательных и нулевых канонических коэффициентов квадратичной формы не зависит от преобразования, с помощью которого квадратичная форма приводится к каноническому виду.
Число положительных канонических коэффициентов квадратичной формы называется положительным индексом инерции квадратичной формы. Число отрицательных канонических коэффициентов квадратичной формы называется отрицательным индексом инерции квадратичной формы. Разность между положительным и отрицательным индексами квадратичной формы называется сигнатурой квадратичной формы. Число ненулевых канонических коэффициентов называется рангом квадратичной формы.
Числовая функция А(х, у), аргументами которой являются всевозможные векторы х и у вещественного линейного пространства L, называется билинейной формой, если для любых векторов х, у и z из L и любого вещественного числа λ выполняются следующие соотношения:
