Начальные условия

В случае бесконечной струны нужно сформулировать только начальные условия в следующем виде:

. (6)

С физической точки зрения первое из этих условий задает смещение каждой точки струны, а второе – скорость каждой точки струны в начальный момент времени. Задача отыскания решения уравнения (4) или (5) при выполнении условий (6) называют задачей Коши.

§ 2. Случай ограниченной струны.

Рассмотрим теперь струну длины l. Для ограниченной струны наряду с начальными условиями надо сформулировать и граничные условия. Существует три основных типа граничных условий.

Граничные условия I рода. В этом случае задаются перемещения на концах струны как функции времени (Рис. 7)

(7)

Е

u

сли на концах струна неподвижно закреплена, то в условиях (6) . Такие условия называют однородными, а само неподвижное закрепление – защемлением.

Рис. 7. Граничные условия первого рода

Рис. 8. Граничные условия второго рода

Граничные условия II рода. В этом случае задаются проекции силы на ось u на концах струны как функции времени. Как мы выяснили, каждая из них равна , поэтому на концах задаются производные u_x как функции времени (Рис. 8)

(8)

Если концы струны свободны, хотя и перемещаются только по вертикали, то в условиях (7) g₁(t) и g₂(t) будут равны нулю.

Граничные условия III рода. В этом случае лучше начать с механического смысла этих условий. Сначала предположим, что концы струны связаны с осью x (см.рис.13), тогда со стороны каждой из пружин на концы струны по закону Гука будут действовать силы пропорциональные смещению u. Поскольку силы, действующие со стороны пружин должны быть равны вертикальным проекциям сил со стороны струны, то можно записать условия на концах следующим образом:

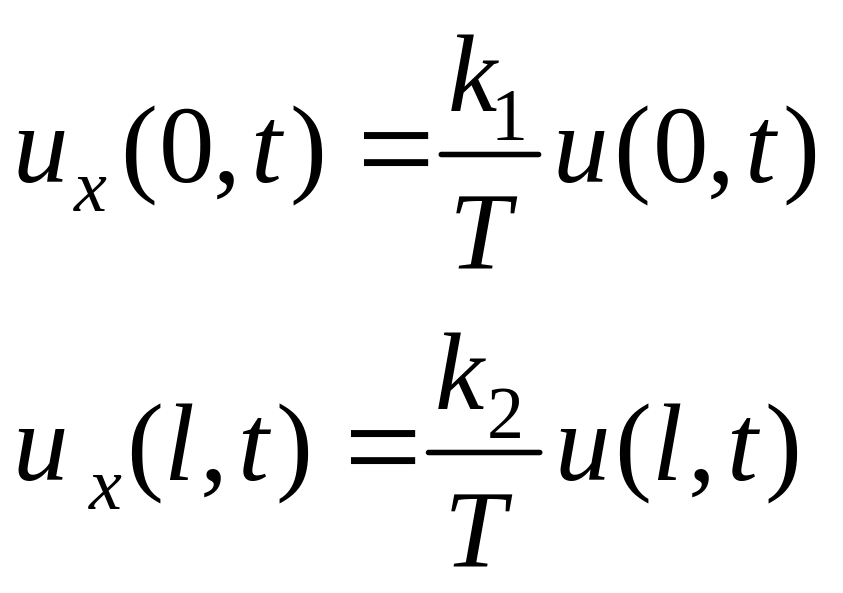, (9)

где k₁ и k₂ – жесткости пружин, прикрепленных к струне на концах струны. Такое граничное условие часто называют упругим закреплением струны в граничных точках

Теперь рассмотрим общий случай, когда один конец пружины прикреплен к струне, а второй движется по вертикали по заданному закону времени θ (t) (Рис. 9). Тогда условия (9) изменятся следующим образом:

(10)

После переноса слагаемых и переобозначений мы получим граничные условия III рода в традиционном виде

(11)

где , (i =1,2)

Рис. 9. Граничные условия третьего рода (частный случай).

Рис. 10. Граничные условия третьего рода (общий случай).

К перечисленным видам граничных условий нужно добавить граничное условие, которое описывает действие на конце струны вертикальной силы, пропорциональной скорости и направленной в противоположном направлении. Такую силу обычно называют силой вязкого трения. Она может создаваться гидравлическим демпфером, соединяющим конец пружины с неподвижной точкой на оси x. Условие такого типа записывается (для левого конца) следующим образом:

(12)

или , где (13)

В некоторых физических задачах приходится прибегать к использованию на разных концах струны разных типов граничных условий. Например, на левом конце задается условие защемления, а на правом упругое закрепление.