§ 7. Поведение потенциала простого слоя при переходе через границу

В отличие от потенциала двойного слоя потенциал простого слоя

(18)

непрерывен в точках поверхности S. Чтобы убедиться в этом для случая гладкой поверхности достаточно установить равномерную сходимость интеграла V(M) в точках поверхности S.

Пусть P₀ – некоторая точка поверхности S. Представим потенциал V(M) в виде суммы

где S₁ – достаточно малая часть поверхности S, содержащаяся в сфере радиуса δ с центром в точке P₀.

Рассмотрим систему координат с началом в точке P₀, у которой ось z направлена по внешней нормали в точке P₀. Пусть M(x, y, z) – произвольная точка, отстоящая от P₀(0,0,0) на расстоянии . Обозначим через S₁' проекцию S₁ на плоскость (x, y), а через – круг радиуса 2δ с центром в точке M' (x, y, 0), целиком содержащий область S₁'. Предполагая ограниченность функции

и принимая во внимание, что

,

где γ - угол, а также, что

,

получим

,

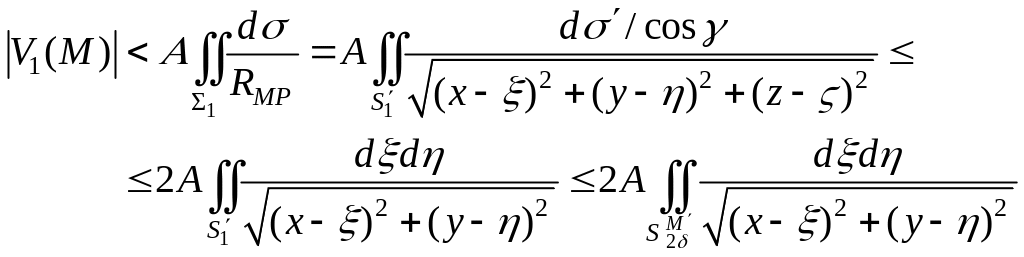при условии, что δ настолько мало, что cos γ >1/2.

Введем теперь в плоскости x, y полярную систему координат (ρ,φ) с началом в точке М'. Тогда последний интеграл легко вычисляется

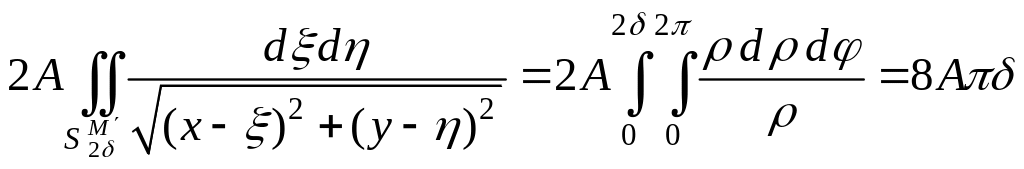
и мы, выбирая δ=ε/8πA, можем окончательно записать

,

если МР₀ < δ. Следовательно, интеграл V(M) равномерно сходится в любой точке и является непрерывной функцией в этой точке.

Обратимся теперь к изучению поведения нормальных производных потенциала простого слоя при переходе через поверхность. Покажем, что они имеют на S, разрыв такого же типа, как и потенциал двойного слоя.

Внешняя и внутренняя нормальные производные функции V(M), т.е. и , определяются следующим образом. Пусть P₀ – некоторая точка S. Из точки P₀ проведем ось z, которую можно направить либо вдоль внешней, либо вдоль внутренней нормали.

Рассмотрим производную в некоторой точке М на оси z. Обозначим и пределы производной при стремлении точки М к точке P₀ с внутренней или с наружной стороны поверхности S. Если ось z направлена по внешней нормали, то это значения называются предельными значениями производной по внешней нормали, если же ось z направлена по внутренней нормали, то это значения называются предельными значениями производной по внутренней нормали в точке P₀.

Исследуем разрывы внутренней нормальной производной потенциала простого слоя на S. Производная в точке М оси z направленной по внутренней нормали, равна

(19)

где ψ – угол между осью z и вектором . Проведем из точки Р (Рис. 35) внутреннюю нормаль PQ и прямую PN, параллельную оси z (т.е. нормали в точке P₀), и обозначим через θ угол NPQ, равный углу между нормалями в точках Р и P₀. Выражение для потенциала двойного слоя W (M) содержит множитель , где . Так как угол MPN равен , то можно показать, что

где Ω двухгранный угол с ребром PQ. Отсюда следует, что

(20)

где W₁(M) – потенциал двойного слоя с плотностью , имеющий разрыв на поверхности S. Очевидно, что интеграл I(M) является функцией, непрерывной в точке Р₀, так как I(M) сходится равномерно в этой точке. Тогда возвращаясь к формуле (20) можем написать

(21)

Обозначим теперь

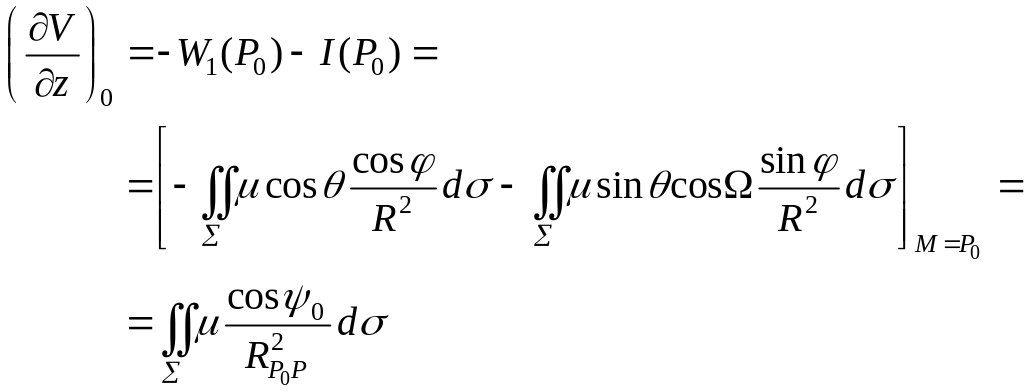
где ψ₀ – угол между осью z и вектором Р₀Р. Замечая далее, что , находим

(22)

так как по условию ось z направлена по внутренней нормали. Если ось z направить по внешней нормали, то знак изменится, и мы получим

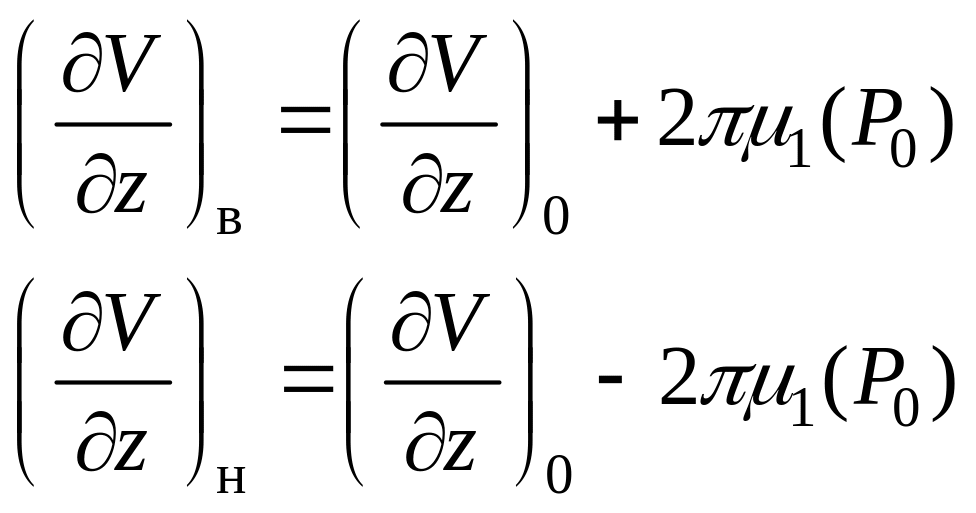(23)

Для случая двух переменных имеют место аналогичные формулы с заменой 2π на π.