§ 4. Трехмерное неоднородное волновое уравнение

Рассмотрим трехмерное неоднородное волновое уравнение

(28)

и будем искать его решение, удовлетворяющее нулевым начальным условиям

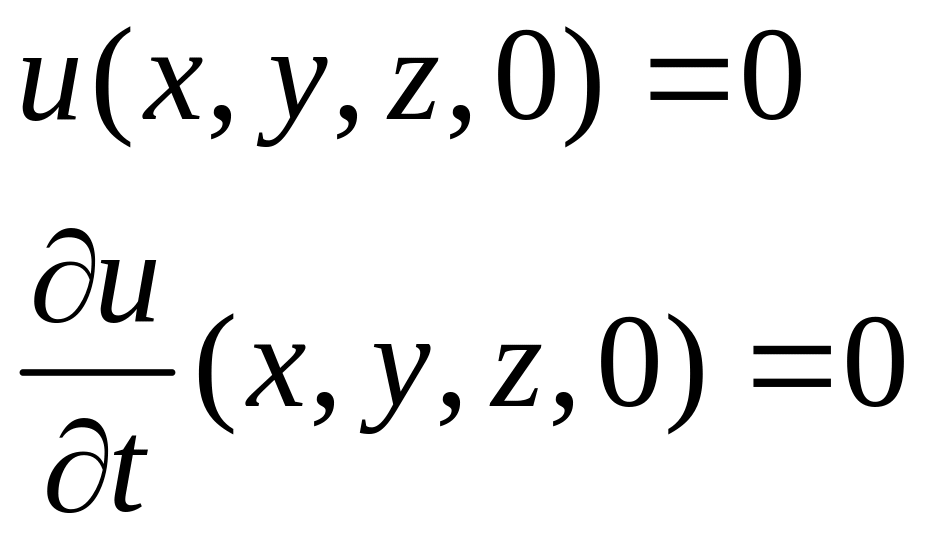(29)

Это означает, что в исходном состоянии описываемый объект не был деформирован и покоился. В этом случае деформации этого объекта в последующие моменты времени будут определяться только внешней силой и механическими свойствами объекта.

Чтобы решить поставленную задачу нужно решить однородное уравнение

(30)

но с ненулевой начальной скоростью, равной внешней силе из уравнения (28) в некоторый момент времени τ : :

(31)

При этом τ становится параметром задачи. Иными словами воздействие внешней силы на объект заменяется на сообщение точкам объекта соответствующей скорости в некоторый

Теперь для решения задачи можно воспользоваться формулой (12) из §1, заменив в ней t на , тогда получим

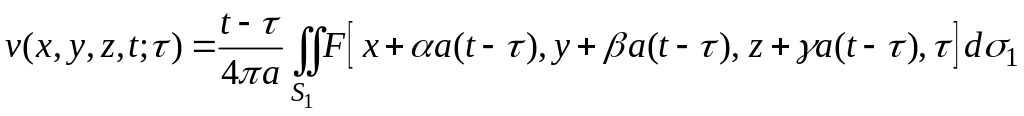? (32)

Теперь покажем, что функция , определенная формулой

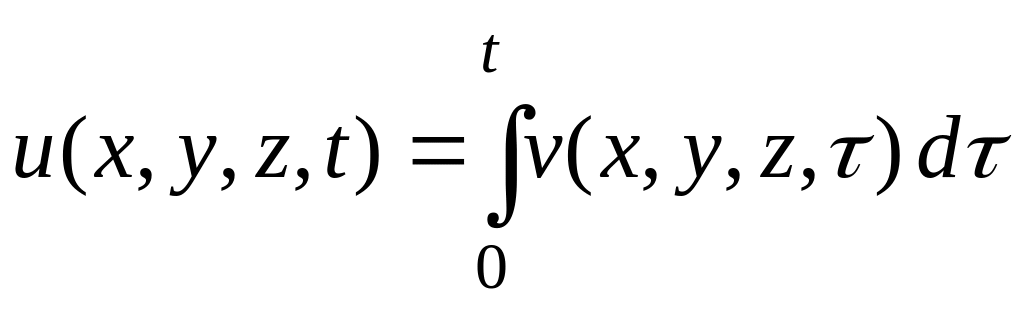, (33)

является решением неоднородного уравнения (28) при нулевых начальных условиях (29). Действительно, из формулы (33) находим

(34)

Дифференцируя теперь выражение (33) по времени, получим

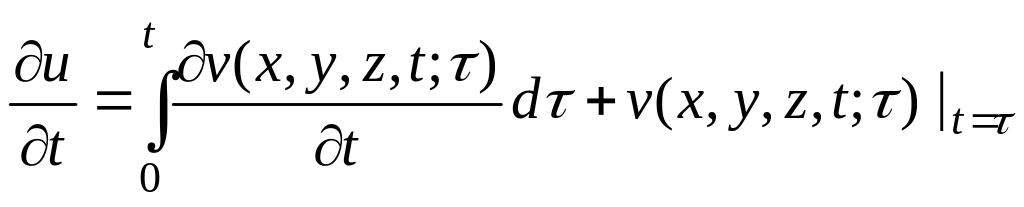, (35)

причем внеинтегральный член при равен нулю в силу первого начального условия (31), т.е.

(36)

Дифференцируя ещё раз по t, будем иметь

, (37)

причем здесь внеинтегральный член при в силу первого начального условия (31) равен , т.е.

(38)

Поскольку функция v удовлетворяет уравнению (30), то (38) можно переписать следующим образом

,

а в силу (33) входящий в это выражение интеграл есть Δu. В итоге получим

,

т.е. функция u удовлетворяет исходному уравнению (28). При этом начальные условия (29) также выполнены в силу (33) и (36).

Подставив в формулу (34) вместо функции её выражение (32), получим

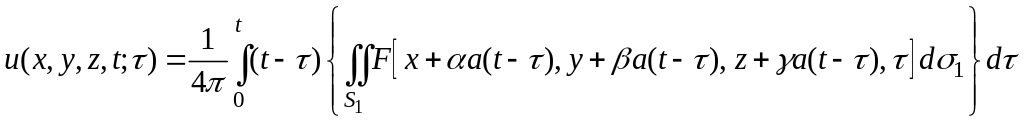
Затем, если введем вместо τ новую переменную интегрирования , то получим

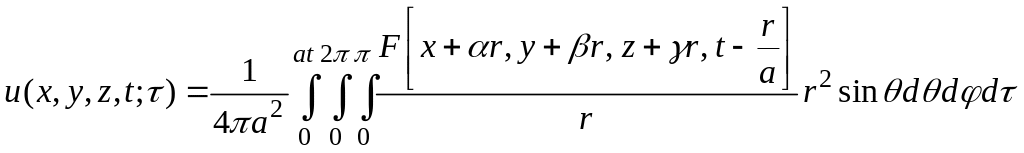
Вводя новые координаты

И учитывая, что , получим

,

и выражение для окончательно запишется в виде

(39)

где D_at – шар радиуса at с центром в точке (x, y, z).

Выражение (39) называют запаздывающим потенциалом, так как при выполнения интегрирования функция g берется не в рассматриваемый момент времени t, а в момент, наступивший раньше на промежуток времени r/a, необходимый для того, чтобы возмущение, распространяясь со скоростью a от точки (ξ, η, ζ ), дошло до точки (x, y, z ).

Аналогичным образом мы можем получить решение для двухмерного волнового уравнения

(40)

с нулевыми начальными данными

(41)

Это решение имеет вид

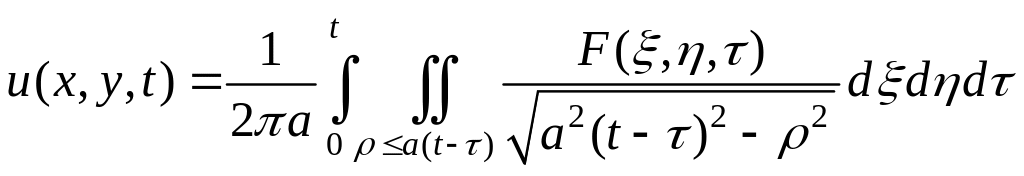(42)

где