20. Функция Дирака. Функция Хевисайда, её производная.
Функция Дирака,
она же дельта функция δ(x):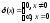
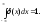
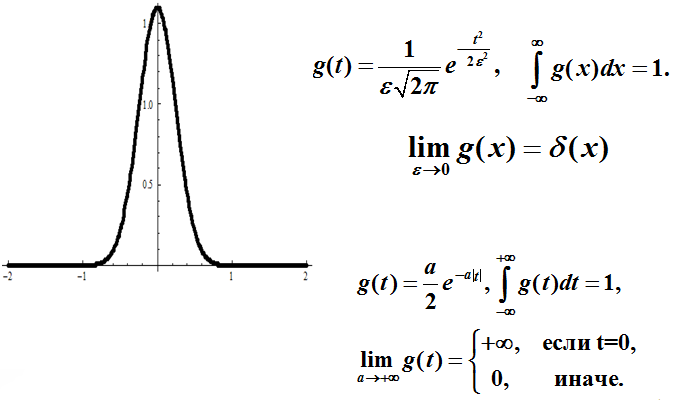
Пример её построения:
δ(x) не является функцией в обычном смысле.
Функция Хевисайда,
она же функция единич-
ного скачка
Ее график:
Производная функции
Хевисайда существует и равна нулю во
всех точках, кроме x=0. В этой точке предел
отношения приращения функции и приращению
аргумента уходит на бесконечность.
Если построить последовательность
кусочно-линейных функций вида,
то наклонные
отрезки графиков выражаются в виде
уравнения пучка прямых, проходящих
через точку А:
Если положить а
= 1, 2, …, ∞,
то кусочно-линейная функция на графике
стремится к функции Хевисайда.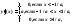
Производные таких функций равны
При а = 1, 2, … получается последова-
тельность
производных, совпадающих с прямоугольными
функциями, при а
∞ они
стремятся к δ-функции.
То есть :
21. Свойства ф-ции Дирака.
1. Фильтрация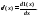 
2. Связь с функцией
Хевисайда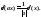 
3. Масштабирование
4. Нечетность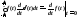 
5. Дифференцирование
Доказательство
5. Продифференцируем
обе части свойства 1
Положим t=0 и получим требуемое свойство.
22. Преобразование Фурье функции Дирака. Обратное преобразование Фурье от постоянной.
К дельта-функции
можно применить преобразование Фурье:
в результате
получается, что спектр (фурье-образ)
δ-функции
является просто константой: 
То есть,
23. Коммутативность оператора свертки. Преобразование Фурье свертки.
В общем случае
сверткой двух функций f(t)
и g(t)
называется интегральное преобразование.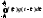
Операция свертки
двух функций обозначается f(t)
*g(t)
или просто f
*g
. Если выполнить замену переменных γ
= t
– τ,
то
dγ
= – dτ
и
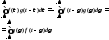
То есть, f *g = g *f – операция свертки коммутативна.
Применим
преобразование Фурье к свертке сигналов,
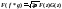
в результате получим равенство:
То есть, применение
преобразования Фурье к свертке сигналов
дает произведение Фурье-образов сигналов
с коэффициентом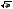 
24. Обратное преобразование Фурье свертки сигналов.
Для обратного
преобразования Фурье от свертки функций
Если к обеим частям
полученного равенства применить прямое
преобразование Фурье, то получим формулу
для преобразования произведения
сигналов 
25. Преобразование Фурье функции единичного скачка.
Производная функции
1(t)
равна δ(t),тогда
интеграл от δ(t)
равен функции единичного скачка 1(t)
: 
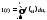
Теперь применяем
свойство 6 преобразования Фурье и,
учитывая, что получаем:
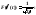
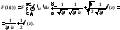
26. Преобразование Фурье тригонометрических функций.
Для некоторых
вещественных функций x(t)
их Фурье-образ X(z)
– тоже вещественная функция. При выводе
преобразования Фурье применялся
интеграл Фурье.
Из формулы
получим
Они называются
соответственно прямым
и обратным косинус-преобразованием.
Косинус-преобразования переводят
вещественную функцию в вещественную.
Аналогично из формулы
получаем прямое
и обратное синус-преобразование
