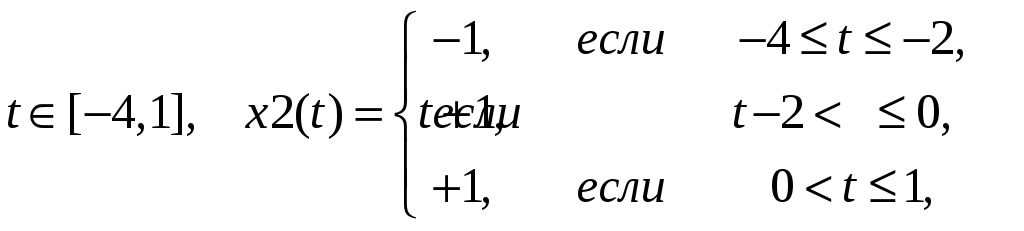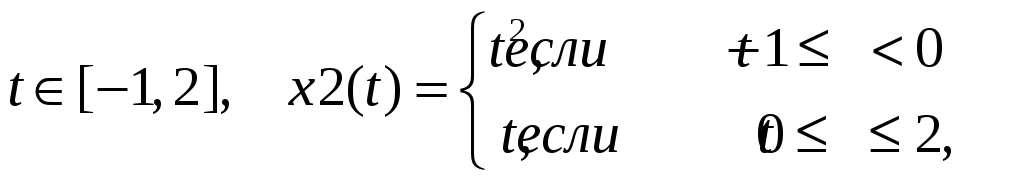Задания по ОТУиС для контрольных для группы 800501

Основы теории управления и системотехника

Задания по контрольной работе

Введение. Модель сигнала, временная и частотная области.

Общение людей может осуществляться разными способами: жестами, письмами, голосом и т.д. Передача и прием сигналов – один из способов обмена информацией. В передаче участвуют хотя бы два устройства: передающее и принимающее. Сигнал передается в некоторой физической среде, это может быть воздух при голосовом общении, при этом звук выражается колебаниями молекул воздуха при сжатии и разряжении слоя воздуха, прилегающего к поверхности колеблющегося тела. Физической средой может быть металлический проводник, здесь сигнал можно передавать разными способами, например, изменением напряжения на двух клеммах передатчика, это изменение передается через два проводника. Еще одна физическая среда – это так называемый эфир – сигнал передается электромагнитными колебаниями.

Во всех случаях информация передается изменением некоторого параметра в зависимости от времени, математически сигнал можно записать как функцию времени x(t). В радиоэлектронике параметром, посредством которого задается сигнал, могут быть различные числовые характеристики электрического тока или электромагнитного поля. Физические способы (?) применения таких характеристик называется модуляцией.

При амплитудной модуляции x(t) может быть напряжением в проводнике.

На физическом уровне любое передающее устройство генерирует непрерывный (математический термин) сигнал, который называется также аналоговым сигналом (термин из радиоэлектроники). Пример такого устройства – тактовый генератор. Измерение непрерывных сигналов приемником, как правило, сопровождается некоторыми необходимыми преобразованиями информации, например, удалением шума. Основная задача этих преобразований – восстановление переданного сигнал как функции от времени с заданной точностью. Цель такого восстановление – корректный прием информации.

В современных системах передачи информации и измерительной техники применяется дискретная форма представления сигналов. В большинстве случаев она дает значительные преимущества при передаче, хранении и обработке информации (высокая помехоустойчивость, вывод принятой информации в цифровой форме, обеспечивающей компактную цифровую индикацию и удобный ввод данных в цифровые вычислительные машины и устройства для обработки данных). Кроме того, она позволяет использовать одни и те же устройства (каналы связи, устройства обработки информации) для большого числа различных информационных систем.

Переход от аналогового представления сигнала (физического уровня) к цифровому (уровень обработки и анализа информации) связан с его дискретизацией по времени и по значению. Например, если исходный сигнал представлен функцией зависимости напряжения от времени, то дискретной форме напряжение будет принимать несколько допустимых значение напряжения, скажем, два значения: -3в и +3в. Решение задачи временной дискретизации (ВД) непрерывных сигналов невозможно без выбора определенной математической модели реального физического сигнала. Модель сигнала должна соответствовать решаемой задаче. Другими словами, особенности математического представления сигнала должны соответствовать объему и характеру передаваемой информации и физическим свойствам устройств.

Обычно сигнал представлен как функции от времени x(t), говорят, что сигнал задан в частотной области. Во многих реальных системах для преобразований и анализа используется спектральная функция F(z), спектральная функция зависит от аргумента z – частоты передачи сигнала. Обычно сигнал передается в некотором интервале частот, спектральная функция задает сигнал в частотной области. Если эти две функции существуют (а для реальных сигналов это так!), то говорят, что спектральная функция F(z) задана в частотной области. Две эти функции могут дать достаточное для многих приложений описание сигнала. Это и есть математическая модель представления сигнала.

Для спектральной функции сигнала F(z) обычно вычисляют амплитудный спектр, энергетический спектр и т.д. Для этой модели мы можем выполнить элементарный анализ системы, например, применяя равенство Парсеваля, найти энергию, которая потребуется для передачи сигнала в некотором частотном диапазоне.

В Задании 1 контрольной работы требуется выполнить элементы спектрального анализа сигнала. В Задании 2 на основе методов Задания 1 требуется выполнить квантование (дискретизацию) сигнала.

Задание 1. Разложение сигнала в ряд Фурье и преобразование Фурье.

1. Разложение сигнала в ряд Фурье.

Ряд Фурье и преобразование Фурье – основные инструменты анализа сигнала в радиоэлектронике. Вначале рассмотрим разложение в ряд Фурье функции x(t).

В основе ряда Фурье лежат тригонометрические ортогональные функции. Величина T является периодом разложения, она выбирается исследователем, если сигнал периодический, то это и есть период сигнала. соответственно ω = 2π/T – частота (угловая скорость) разложения.

Ряд Фурье, кроме первого члена, состоит из выражений

говорят, что это k-й член разложения, эти функции называются базисными функциями Фурье. Базисных функций разложения ортогональны, по определению означает, что

Легко проверить ортогональность базисных функций Фурье интегрированием. Например, (используя формулу произведения синусов)

Коэффициенты A_k, B_k ряда Фурье вычисляются с применением свойства ортогональности базисных функций.

Ф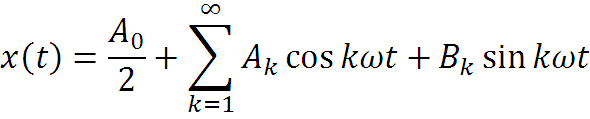 ункция f(t) называется четной, если f(-t) = f(t). Функция f(t) называется нечетной, если f(-t) = -f(t). Синус – четная функция, косинус – нечетная.

Ряд Фурье разложения нечетной функции не содержат базисных функций cos(·), то есть, все коэффициенты A_k равны нулю. При разложения четной функции ряд Фурье не содержат базисных функций sin(·), B_k равны нулю.

В выражении (2) интегралы для реальных задач обычно не являются табличными. Вычислять их следует приближенными методами, например, методом прямоугольников.

Аргументы kω тригонометрических функций в разложении представляют собой угловую скорость, можно сказать, частоту колебаний. Поэтому число

характеризует вклад (суммарный вклад функций косинуса и синуса) частоты kω в амплитуду сигнала. Множество всех чисел C_k называется спектром сигнала. Заметим, что спектр сигнала зависит от периода T разложения сигнала.

1.2. Преобразование Фурье.

В разложении в ряд Фурье требуется задавать период T сигнала. Это неудобно, так как, во-первых, период сигнала бывает неизвестным и необходимо находить его, во-вторых, бывают и непериодические сигналы. Для того, чтобы исследовать сигнал без использования периода, математически было выведено преобразование Фурье, это интегральное преобразование сигнала. Если период T стремится к бесконечности, то ряд Фурье стремится к интегралу, который и дает преобразование Фурье. Однако, при этом пришлось перейти к комплексным числам и в общем случае преобразование Фурье переводит обычную вещественную функцию от вещественного аргумента в комплекснозначную функцию от вещественного аргумента. Преобразованием Фурье сигнала x(t) называется

Функция X(z) называется Фурье-образом сигнала x(t), краткая запись: . По аналогии в разложением в ряд, аргумент z играет роль частоты передачи сигнала. Говорят, что X(z) представляет сигнал в частотной области, а функция X(z) – это спектр частот сигнала, спектральная функция, или просто спектр.

Если известна спектральная функция X(z), то из нее математически можно вывести функцию сигнала во временной области, обратным преобразованием Фурье называется интегральное преобразование

Краткая запись: .

По аналогии со спектром амплитуд |X(z)|, называется амплитудной функцией, или спектром амплитуд, а Arg(X(z)) фазовой функцией для X(z). Вычислить интегралы можно обычными математическими методами, в том числе и приближенными. Для рассматриваемых прямого и обратного преобразования Фурье имеются таблицы. Кроме того, выводятся свойства преобразований, упрощающие вычисление интеграла.

1.3. Свойства преобразования Фурье.

1. Линейность

F(a·f(t) + b·g(t)) = a·F(f(t)) + b·F(g(t)).

2. Умножение аргумента

3. Свойство сдвига

4 . Преобразование производной

5. Преобразование интеграла

1.4. Таблица преобразований Фурье

x(t)	X(z)
с
1(t)
sin ωt
cos ωt
R(a,ε,t)

1.5. Задание 1. Согласно варианту разложить в частичный ряд Фурье для k = 0, 1, 2,…,6 два заданных сигнала x1(t) и x2(t). Сигнал x1(t) задан на всей числовой оси, найти его период. Сигнал x2(t) задан на указанном отрезке, при разложении считать, его период равен длине отрезка. Найти спектры сигналов x1(t) и x2(t).

Для каждого сигнала построить его график, графики разложений и спектры.

Если вы можете, то используйте формулу Ньютона (вычисление определенного интеграла при помощи первообразной). Если не можете найти первообразную, применяйте приближенные методы вычисления определенного интеграла, например, метод прямоугольников. Для этого напишите программу на языке высокого уровня. Инструментальные системы Matlab, Matcad и другие для вычислений не применять (их можно использовать только для построения графиков).

1.6. Задание 2. Согласно варианту найти преобразование Фурье для для сигнала x2(t), заданого на указанном отрезке. Найти амплитудный спектр сигнала x2(t).

Построить график сигнала и график его амплитудного спектра.

Варианты. Разложение в ряд Фурье (оба сигнала). Преобразование Фурье (сигнал x2(t)).

№	Сигнал x1(t)	Сигнал x2(t)
1	sin2(4t+1)
2	sin3(2t+0.5)
3	sin4(t/2 - 0.5)
4	|sin(2t-4)| (абсолютная велич)
5	|cos(3t+2)|
6	|sin3(2t+2)|
7	e3sin(3t-1)
8	e2sin(2t+3)
9	e-sin(2t-3)
10	e-cos(2t-2)
11	ecos(2t-3)
12	ecos(t/2-3)
13	1/(sin(2t)+2)
14	2/(sin(4t-0.5)+5)
15	1/(sin2(-2t-1)+1)
16	1/(cos(4t-0.5)+3)
17	1/(cos(2t-0.5)+3)
18	1/(cos2(3t-0.7)-2)
19	1/(cos3(5t-0.5)-2)
20	1/(cos(2t-0.1)-1.5)
21	esin(2t-1)+4
22	esin(2t-4)+1
23	e-sin(1.5t-0.5)
24	ecos(2t-3)+2
25	e-cos(5t-3)-1
26	e-cos(3t-1)+0.1
27	e-sin(5t-3)+0.3
28	t-[t] (целая часть числа)
29	ln(sin(2t)+1.5)
30	ln(sin(3t)+2.5)
31	ln(sin2(2t)+1.5)
32	ln(sin3(4t)+1.5)
33	ln(cos(2t)+1.5)
34	ln(cos2(2t)+2.5)
35	ln(cos(2t)+5)
36	ln(cos2(4t)+1.5)
37	ln(cos(5t)+1.5)
38	arcsin(sin(t+1))
39	arcsin(sin2(t+1))
40	arccos(sin2(t+1))
41	arccos(2sin(t))
42	arccos(-3sin(t))
43	arctg(sin2(t+1)/2)
44	Sgn(sin(t+1))
45	Sgn(sin(2t+1))
46	Sgn(sin2(2t+2))
47	Sgn(sin3(t-1))
48	Sgn(sin(t/2+1))
49	Sgn(sin(t/3+1))
50	Sgn(sin(t/4+1))