16. Кинетическая система материальной точки и системы. Кинетическая энергия в простейших случаях движения тела. Теорема Кенига.

Изменение кинетической энергии системы равно работе всех внутренних и внешних сил, действующих на тела системы.

Поступательное движение.

В этом случае скорости всех точек тела одинаковы. Тогда:   – кинетическая энергия тела при поступательном движении равна половине произведения массы тела на его скорость.

Вращательное движение

В этом случае   . Тогда

– кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости.

Теоре́ма Кёнига

Кинетическая энергия механической системы есть энергия движения центра масс плюс энергия движения относительно центра масс:

T=T0+Tr{\displaystyle {T\;=\;T_{0}+T_{r}}\;,}

Где T - {\displaystyle T} TTTTTTtTTTTtt полная кинетическая энергия системы, {\displaystyle T_{0}}T0 — кинетическая энергия движения центра масс, {\displaystyle T_{r}}Tr — относительная кинетическая энергия системы^[2].

Иными словами, полная кинетическая энергия тела или системы тел в сложном движении равна сумме энергии системы в поступательном движении и энергии системы в её сферическом движении относительно центра масс.

Более точная формулировка: полная кинетическая энергия всей системы равна сумме кинетической энергии всей массы системы, сосредоточенной в ее центре масс и движущейся со скоростью центра масс плюс кинетическая энергия той же системы в ее относительной системе относительно центра масс

17. Теорема об изменении кинетической энергии материальной точки и системы

18. Потенциальное силовое поле и силовая функция. Потенциальная энергия. Закон сохранения механической энергии

Силовым полем называется часть пространства, в котором на материальную точку действует сила, зависящая от координат точки и времени

Если сила явно не зависит от времени, то силовое поле называется стационарным. Стационарное силовое поле называется потенциальным, если проекции силы  на оси Ох, Оу, Oz можно выразить через скалярную функцию  по формулам

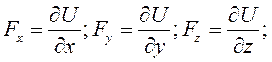 (I) т.е.

Функция  называется силовой функцией. Из (I) следует, что силовая ф-я U определяется с точностью до аддитивной постоянной.

Потенциальной энергией материальной точки в данной точке потенциального силового поля называют работу, производимую силой, действующей на точку в потенциальном силовом поле, при её перемещении из рассматриваемой точки поля  в начальную  ., условно принимаемую за нулевую

Потенциальная энергия. — скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в поле консервативных сил.

 Закон сохранения механической энергии, для любой замкнутой системы полная механическая энергия остается постоянной при любых взаимодействиях тел внутри системы. То есть энергия не возникает из ниоткуда и в никуда не исчезает. Она лишь переходит из одной формы в другую. Это справедливо для замкнутых систем, в которых энергия не поступает из вне, и не уходит из системы наружу.

 Приближённым примером замкнутой системы может служить падение груза относительно большой массы, и малых размеров на землю с небольшой высоты. Допустим, что груз зафиксирован на некоторой высоте. При этом он обладает потенциальной энергией. Эта энергия зависит от его массы и высоты, на которой находится тело.