5. Вынужденные колебания материальной точки без учёта сил сопротивления. Коэффициент динамичности.
Рассмотрим важный случай колебаний,
возникающих, когда на точку кроме
восстанавливающей силы F
действует ещё периодически изменяющаяся
со временем сила Q, проекция
которой на ось Ох равна:
Возмущающая сила по данному уравнению
называется гармонической.
Эта сила называется возмущающей силой,
а колебания, происходящие при действии
такой силы, называются вынужденными.
Величина
является частотой возмущающей силы
Дифференциальное уравнение вынужденных колебаний точки при отсутствии сопротивления
Коэффициент динамичности:
Безразмерный коэффициент
η
называют коэффициентом динамичности.
Он показывает во сколько раз амплитуда
вынужденных колебаний В (т.е. максимальное
отклонение точки от центра колебаний)
больше статического отклонения
, и зависит от отношения частот z.
6. Движение материальной точки в условиях резонанса
В случае, когда
,
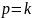т.е. когда частота возмущающей силы
равна частоте собственных колебаний,
имеет место так называемое явление
резонанса.
Резонанс - это резкое возрастание амплитуды вынужденных колебаний. Возникает, когда частота собственных колебаний совпадает с частотой вынуждающей силы
Размахи вынужденных колебаний при резонансе будут со временем неограниченно возрастать
7. Вынужденные колебания материальной точки при сопротивление пропорциональном скорости.
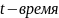
8. Дифференциальные уравнения движения системы материальных точек. Интегральные характеристики системы
Интегральные характеристики (не уверен): В учебнике Тарга нет, в инете много мусора
9. Общие теоремы динамики системы. Теорема о движении масс системы. Закон сохранения движения центра масс
ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС МЕХАНИЧЕСКОЙ СИСТЕМЫ. Центр масс механической системы движется как точка, масса которой равна массе всей системы M=Σmi, к которой приложены все внешние силы системы:
или в координатной форме:
где
-
ускорение центра масс и его проекции
на оси декартовых координат;
внешняя
сила и ее проекции на оси декартовых
координат.
Если сумма внешних сил, действующих на систему, равна нулю, то центр масс такой системы движется с постоянной скоростью, т. е. равномерно и прямолинейно.
10. Общие теоремы динамики системы. Теорема об изменении количества движения материальной точки и системы. Закон сохранения количества движения в системе.
1
.
Количество движения замкнутой системы
с течением времени не изменяется:
dK/dt
= 0 или K= SKi = Smivi = const
Это один из
основных законов природы, вытекающий
из однородности пространства.
2. Закон сохранения количества движения показывает, что взаимодействие тел, составляющих замкнутую систему, приводит только к обмену количествами движения между этими телами, но не может изменить движения системы как целого: при любом взаимодействии между телами, образующими замкнутую систему, скорость движения центра инерции этой системы не изменяется, т. е. dvc/dt = 0 где vc — скорость центра инерции.
1
1.
Теорема
импульсов для материальной точки и
системы
12. Теорема об изменении момента количества движения. Закон сохранения главного момента количества движения системы.
13. Применение теоремы моментов к твёрдому телу, вращающемуся вокруг неподвижной оси.
14. Понятия о моментах инерции твёрдого тела. Момент инерции твёрдого тела, вращающегося вокруг неподвижной оси. Теорема Штейнера-Гюйгенса.
15. Элементарная и полная работа силы. Мощность. Работа внутренних сил. Работа равнодействующей силы.
Элементарная работа силы равна произведению элементарного перемещения на проекцию силы на это перемещение.
|
Элементарная работа силы равна скалярному произведению элементарного импульса на скорость точки её приложения.
|
Полную работу
силы 
на
перемещении точки из положения 
в
положение 
определяют
как предел суммы её элементарных работ,
т.е.
Если же сила является функцией времени (переменная сила) то работа силы на промежутке времени от 0 до t, соответствующем точкам и , определяется выражением
Работа силы зависит от характера движения точки приложения силы. Так, А = 0, если сила приложена к неподвижной точке или к точке, скорость которой во время движения равна нулю (например, МЦС)
Работа равнодействующей силы.
Рассмотрим
систему сил, приложенную к рассматриваемой
точке. Эта система имеет равнодействующую 
,
причём
Тогда работа силы на перемещении точки из в текущее положение М равна алгебраической сумме работ составляющих сил на том же перемещении:
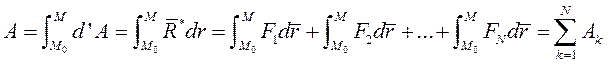
Мощность.
Отношение элементарной работы силы к промежутку времени, за которое оно произошло, называется мощностью.
Так
как 
то
Мощность силы равна скалярному произведению силы на скорость точки её приложения.
Если нагруженное тело находится в равновесии, то внутренние силы равны по значению внешним силам и противоположны им по направлению. Очевидно, что они препятствуют развитию деформации. Работа внутренних сил (U), с учетом их направления по отношению к деформации, всегда является отрицательной.
Работа внешних сил равна взятой с обратным знаком работе внутренних сил:
.