Экзаменационный билет № 14

Использование рядов для аппроксимации функций. Схема Горнера

Использование рядов для равномерной аппроксимации. Возможность построения многочлена, равномерно приближающего данную функцию следует из теоремы Вейерштрасса об аппроксимации. В частности, если f(x) на отрезке [a,b] разлагается в равномерно сходящийся ряд, то в качестве аппроксимирующего многочлена можно взять частичную сумму ряда Маклорена. Вместо ряда Маклорена для равномерной аппроксимации могут использоваться ряды Тейлора, многочлены Чебышева, Лежандра и т.п..

Рассмотрим такие трансцендентные функции, которые являются суммами своих рядов Маклорена:

(2.5)

Беря несколько первых членов ряда Маклорена, получаем приближенную формулу:

(2.6)

где,

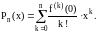(2.7)

Погрешность. Остаток ряда представляет собой ошибку при замене f(x) многочленом P_n(x), т.е. определяет абсолютную погрешность вычисления f(x) с использованием формулы (2.6). Для ряда (2.5) абсолютная погрешность будет не больше по абсолютной величине остаточного члена ряда Маклорена в форме Лагранжа:

(2.8)

где  некоторая неизвестная точка на отрезке [0,x].

Разложение элементарных функций в ряд Маклорена:

(2.9)

(2.10)

где  - точка на отрезке [0,X].

Схема Горнера. Для вычисления полиномов вида

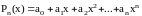(2.11)

часто применяется следующая формула

(2.12)

которая позволяет значительно сократить количество выполняемых арифметических операций. Прием с помощью которого многочлен (2.11) представляется в виде (2.12) называется схемой Горнера.

Вычисление значений многочлена по схеме Горнера требует выполнения n умножений и n-k сложений, где k – число коэффициентов ai, равных нулю. Если a0 = 1, то требуется выполнить n-1 умножений. Показано, что для многочленов общего вида нельзя построить схему более экономичную в смысле числа операций, чем схема Горнера.

Основные типы матриц систем линейных уравнений. Определитель. Необходимое и достаточное условие единственности решения системы линейных уравнений

Типы матриц:

• Если m = n, то матрица называется квадратной порядка n;

• Если m != n, то матрица называется прямоугольной. В частности, матрица 1х n называется вектором-строкой, а m x 1 – вектором-столбцом;

• Диагональная (элементы присутствуют только на главной диагонали; остальные нули);

• Единичная (на главной диагонали располагаются единицы);

• Нулевая (все элементы равны нулю).

Определителем ( детерминантом ) матрицы А порядка n называется число _n (detA) равное:

где индексы ,,...,, пробегают все возможные n! перестановок чисел 1,2,...n; k- число инверсий в данной перестановке ( инверсия - количество всех возможных пар из индексов ,,...,, для которых выполняется условие, что в паре первый индекс больше второго, например, если > и ,<..., то в перестановке всего одна инверсия).

Также используется следующее определение детерминанта, которое эквивалентно предыдущему:

где - определитель матрицы порядка (n-1), образованной из матрицы A вычеркиванием первой строки и i-ого столбца.

Для существования единственности решения системы (2.1) необходимо и достаточно выполнения условия det A0.

Методы Адамса для решения задачи Коши

Метод Адамса-Бошфорта – экстраполяционная формула

Метод Адамса-Моултона – интерполяционная формула