Экзаменационный билет № 10

Корректность вычислительных алгоритмов. Три условия корректности вычислительного алгоритма. Обусловленность вычислительного алгоритма

Корректность вычислительных алгоритмов

1. Результат получен после конечного числа шагов

2. Результат устойчив к малым возмущения входных данных

3. Результат обладает вычислительной устойчивостью.

Метод Монте-Карло для задач вычисления кратных интегралов

Формула (5.33) непосредственно обобщается на кратные интегралы

 

,

 

где   – объем области интегрирования. Например, для двукратного интеграла с прямоугольной областью интегрирования имеем

 

.   

Модификации метода Эйлера второго порядка точности для дифференциального уравнения первого порядка

Метод трапеции. В этом методе решение имеет вид:

(2.9)

Этот метод неявный, т.к. для определения значений y_i+1 необходимо решать нелинейное уравнение (2.9). Метод трапеций имеет второй порядок точности по h.

метод Эйлера-Коши. Данный метод является прямым методом второго порядка точности:

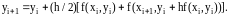(2.10)

Экзаменационный билет № 11

Требования, предъявляемые к вычислительным алгоритмам. Требования к программным реализациям вычислительной задачи

Требования к вычислительным алгоритмам

1. Экономичность(число элементарных операций)

2. Надлежащая точность(решение задачи с заданной или приемлемой точностью)

3. Экономия памяти(-)

4. Простота

Требования к программным реализациям алгоритмов

1. Надежность(без ошибок)

2. Работоспособность

3. Переносимость

4. Поддерживаемость

5. Простота

Система линейных уравнений. Абсолютная погрешность и невязка решения системы линейных уравнений

Система уравнений вида:

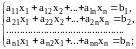(2.1)

или в сокращенной записи:

называется линейной алгебраической системой из n уравнений с n-неизвестными x_i (i=1,...,n). В матричной форме она записывается следующим образом:

(2.2)

где A - квадратная матрица, и - векторы столбцы вида:

Методы Рунге - Кутты второго порядка точности для решения задачи Коши

расчетам формулы метода Рунге-Кутты второго порядка точности имеют следующий вид:

(2.12)

Данный метод является двух этапным. Вначале вычисляется значение k⁽¹⁾, а затем значения k⁽²⁾.

При =1 формулы (2.12) дают метод Эйлера-Коши, при =1/2 - усовершенствованный метод Эйлера.

Экзаменационный билет № 12

Приближение функций. Среднеквадратичное и равномерное приближение

1 Версия

Аппроксимация состоит в том, что данную функцию f(x) приближенно заменяют (аппроксимируют) некоторой другой функцией, так, чтобы отклонение (x) от f(x) в заданной области [a,b] было минимально возможным, при этом функцию f(x) называют аппроксимируемой, а функцию (x) аппроксимирующей.

При приближении на непрерывном множестве точек отрезка [a,b] аппроксимацию называют непрерывной (или интегральной). Если приближение строится на заданном дискретном множестве точек {x_i} i=0,1,... отрезка [a,b], то аппроксимацию называют точечной.

Если аппроксимирующая функция (x) строится для всего отрезка [a,b] на котором задана функция f(x), то говорят о глобальной аппроксимации, если же весь отрезок [a,b] разбит на частичные отрезки и на каждом используется своя аппроксимирующая функция, то говорят о локальной аппроксимации.

Равномерное и среднеквадратичное приближения. Если приближение строится таким образом, что величина отклонения (модуль разности двух функций f(x) и (x)) удовлетворяет условию

(2.2)

то такое приближение (2.2) называют равномерным приближением.

Часто используется среднеквадратичное приближение функции f(x) функцией (x). Здесь стараются получить минимальную величину среднеквадратичного значения модуля разности аппроксимируемой и аппроксимирующей функций на всем отрезке [a,b]:

(2.3)

Первая формула используется при непрерывной аппроксимации, а вторая при дискретной аппроксимации.