Экзаменационный билет № 8

Обусловленность вычислительной задачи. Абсолютное и относительное число обусловленности

Обусловленность вычислительной задачи — чувствительность ее решения к малым входным данным.

Выделение весовой функции при численном интегрировании

Метод Эйлера решения дифференциального уравнения первого порядка. Погрешность метода Эйлера

Дифференциальное уравнение первого порядка:

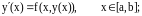(2.4)

В методе Эйлера решение уравнения (2.4) представляется следующим образом:

(2.6)

где , - начальная точка, - шаг между узлами x_i и x_i+1, - значение искомой функции y(x) в узле x_i, . При i=0 имеем:

(2.7)

где y₀=y(x₀) - начальное значение искомой функции y(x).

Абсолютная погрешность метода Эйлера на n шаге равна:

(2.8)

где c₁ и c₂ - константы, R₀ - погрешность начального приближения.

Согласно (2.8) метода Эйлера имеет первый порядок точности.

Экзаменационный билет № 9

Вычислительные методы. Классификация вычислительных методов. Устойчивость и сходимость численных методов

Вычислительные методы — методы, которые используются в вычислительной математике для преобразования задач к виду, удобному для реализации на ЭВМ.

Классификация:

1. Методы эквивалентных преобразований(замена исходной задачи на другую, имеющую тоже решение)

2. Методы аппроксимации(замена исходной задачи на другую, решение которой в определенном смысле близко к решению исходной задачи. Погрешность аппроксимации)

Метод сходится, если погрешность аппроксимации стремится к нулю при стремлении параметров метода к некоторому предельному значению.

3. Прямые методы(метод позволяет получить решение после конечного числа элементарных операций)

4. Итерационные методы(построение последовательных приближений к решению задачи)

Метод сходиться, если процесс не бесконечен.

5. Методы статистических испытаний(основанные на моделировании случайных величин и построении статистических оценок решения задач)

Кратные интегралы

Задача Коши для дифференциального уравнения первого порядка. Теорема существования решения задачи Коши. Интегральные кривые

Обыкновенным дифференциальным уравнением называется уравнение, которое содержит производные от искомой функции y(x):

(2.1)

где x - независимая переменная, (n) - порядок производной. Наивысший порядок n, входящий в уравнение (2.1) называется порядком дифференциального уравнения.

Общее решение дифференциального уравнения имеет вид:

(2.2)

где c₁,c₂,...,c_n - произвольные постоянные. Их количество определяется порядком уравнения.

Если значения c₁,c₂,...,c_n известны и соответственно равны , то из (2.2) получаем частное решение:

Значения определяются из условий, которые называются дополнительными условиями для уравнения (2.1).

Графики частных решений называются интегральными кривыми для данного дифференциального уравнения. Общее решение можно представить в виде семейства интегральных кривых.

Если дополнительные условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задачи Коши называются начальными условиями, а точка x=x₀, в которой они задаются - начальной точкой.

Если дополнительные условия задаются в двух точках a и b - “краях” отрезка [a,b], где ищется решение, то такая задача называется краевой задачей.

Дифференциальное уравнение первого порядка:

(2.4)

при заданных начальных условиях y(x₀)=y₀ называется задачей Коши для дифференциального уравнения первого порядка.

Если мы имеем систему дифференциальных уравнений первого порядка, то задачу Коши удобно записать в векторной форме:

Теорема существования решения задачи Коши

Интегральные кривые