
- •Экзаменационный билет № 1
- •Экзаменационный билет № 2
- •Экзаменационный билет № 4
- •Экзаменационный билет № 6
- •Экзаменационный билет № 7
- •Экзаменационный билет № 8
- •Экзаменационный билет № 9
- •Экзаменационный билет № 10
- •Экзаменационный билет № 11
- •Экзаменационный билет № 12
- •1 Версия
- •2 Версия
- •Экзаменационный билет № 13
- •Экзаменационный билет № 14
- •Экзаменационный билет № 15
- •Экзаменационный билет № 16
- •Экзаменационный билет № 18
- •Экзаменационный билет № 20
- •Экзаменационный билет № 21
- •Экзаменационный билет № 22
- •Экзаменационный билет № 23
- •Экзаменационный билет № 25
- •1 Версия
- •2 Версия
- •Экзаменационный билет № 26
- •Экзаменационный билет № 28
- •Экзаменационный билет № 29
- •Экзаменационный билет № 30
Экзаменационный билет № 6
Точность и диапазон представления вещественных чисел на ЭВМ
Вещественные числа обычно представляются в виде чисел с плавающей запятой. Числа с плавающей запятой — один из возможных способов представления действительных чисел, который является компромиссом между точностью и диапазоном принимаемых значений.
Число
с плавающей запятой состоит из набора
отдельных двоичных разрядов, условно
разделенных на так называемые знак
(англ. sign),
порядок
(англ. exponent)
и мантиссу
(англ. mantis).
В наиболее распространённом формате
(стандарт IEEE 754) число с плавающей запятой
представляется в виде набора битов,
часть из которых кодирует собой мантиссу
числа, другая часть — показатель степени,
и ещё один бит используется для указания
знака числа (![]() — если число положительное,
— если число положительное,
![]() —
если число отрицательное). При этом
порядок записывается как целое число
в коде
со сдвигом,
а мантисса — в нормализованном
виде,
своей дробной частью в двоичной системе
счисления. Вот пример такого числа из
—
если число отрицательное). При этом
порядок записывается как целое число
в коде
со сдвигом,
а мантисса — в нормализованном
виде,
своей дробной частью в двоичной системе
счисления. Вот пример такого числа из
![]() двоичных
разрядов.
двоичных
разрядов.
Правило Рунге для задачи численного интегрирования. Уточнение по Ричардсону
Пусть I - точное значение интеграла, Ih - значение интеграла, вычисленное по квадратурной формуле с шагом h, а Ih/2- значение того же интеграла, вычисленное для шага h/2.
Можем записать:
 (2.15)
(2.15)
где c - константа.
Величина chk- называется главной частью погрешности квадратурной формулы с порядком точности k по шагу h. Остальная часть погрешности обозначена как 0(hk+1) и имеет порядок k+1.
Вычитая из первого уравнения (2.15) второе получаем соотношение, которое с точностью порядка 0(hk+1) позволяет вычислить значение главной части погрешности:
 (2.16)
(2.16)
Данная формула называется практической оценкой погрешности по правилу Рунге:
Подставляя (2.16) в первую формулу (2.15) получаем формулу для уточнения значение интеграла по Ричардсону:
 (2.17)
(2.17)
Для формул прямоугольников, трапеций и ячеек имеем k=2, для формул Симпсона - k=4.
Полиномы Лежандра
Экзаменационный билет № 7
Корректность вычислительной задачи. Существование, единственность и устойчивость решения
Вычислительная задача называется корректной:
Решение существует при любых входных данных
Решение единственно
Решение устойчиво по отношению к малым возмущения входных данных(погрешность решения стремится к нулю, когда погрешность входных данных стремится к нулю.).

Основные квадратурные формулы (прямоугольников, трапеций, Симпсона)
Основные квадратурные формулы. Для вычисления определенных интегралов используется приближенное соотношение:
 (2.3)
(2.3)
которое называется квадратурной формулой с узлами i и весами qi.
В формуле (2.3) интеграл приближенно заменяется конечной суммой, члены которой представляют произведение значений функций в некоторых узлах на некоторую величину. Наиболее часто используются следующие квадратурные формулы:
а) формула прямоугольников:
 (2.4)
(2.4)
где
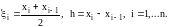
Для всего отрезка [a,b] имеем:
 (2.5)
(2.5)
Погрешность формулы (2.5), полученная с помощью ряда Тейлора равна:
 . (2.6)
. (2.6)
 -
максимальное значение второй производной
на отрезке [a,b].
-
максимальное значение второй производной
на отрезке [a,b].
б) формула трапеции:
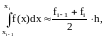 (2.7)
(2.7)
где fi=f(xi), i=1,...n.
Для всего отрезка имеем:
 (2.8)
(2.8)
при этом погрешность равна:
 .
.
в) формула Симпсона (формула парабол):
 (2.9)
(2.9)
Для всего отрезка:
 (2.10)
(2.10)
где

Погрешность формулы Симпсона равна:
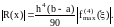 (2.11)
(2.11)
Общее и частное решение дифференциального уравнения. Дополнительные условия
См. билет 9
