Экзаменационный билет № 28

Точность и диапазон представления вещественных чисел на ЭВМ

Метод деления отрезка пополам для задачи минимизации. Метод золотого сечения

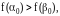Метод деления отрезка пополам. На отрезке выбирается две точки: . Вычисляются значения и Если то точка минимума находится на отрезке если то точка минимума находится на отрезке , т.к. функция является унимодальной. Отрезок с точкой минимума принимается за новый отрезок на котором опять выбираются две точки и т.д., до отрезка длина которого .Следовательно: .

Метод золотого сечения. Золотым сечением отрезка называется деление отрезка на две части, так что отношение длины всего отрезка к длине большей части равно отношению большей части к меньшей (принцип подобия). Золотое сечение отрезка можно произвести двумя симметрично расположенными точками:

(2.5)

где

Сечение называется золотым, потому, что точка x₁ в свою очередь производит золотое сечение отрезка [a,x₂], а точка x₂ - золотое сечение отрезка [x₁,b].

Замена задачи Коши для дифференциального уравнения высокого порядка задачей Коши для системы дифференциальных уравнений первого порядка

Экзаменационный билет № 29

Использование рядов для аппроксимации функций. Схема Горнера

См. билет №14

Аппроксимация производных конечными разностями. Погрешность аппроксимации. Главный член погрешности

Производной функции y=f(x) называется предел:

(2.1)

Для приближенного вычисления производной используется формула:

, (2.2)

где x - некоторое конечное число.

Разностные соотношения, в которых разность между любыми значениями аргумента является конечной величиной, называются конечными разностями. Поэтому соотношение (2.2) также называют аппроксимацией производной с помощью конечных разностей.

Пусть известны значения функции y₀,y₁,...,y_i,...,y_n, вычисленные или заданные таблицей в точках x₀,x₁,...,x_i,...,x_n. Точки x₀,x₁,...,x_i,...,x_n называются узлами, а разность между соседними значениями аргумента называется шагом h_i=x_i=x_i-x_i-1, i=1,...,n. Весь набор узлов называется сеткой. Если величина шага между узлами постоянна, то говорят, что узлы x₀,x₁,...,x_i,...,x_n образуют равномерную сеткой с шагом h.

Для вычисления производной yi в точке точки x_i по формуле (2.2) можно использовать левую разность:

(2.3)

правую разность:

(2.4)

центральную разность:

(2.5)

При численном дифференцировании с использованием приближенной формулы (2.2), например, по формулам (2.3-2.5), естественно возникает погрешность: R(x,h)=y(x)-y_h(x), где y(x) - точное значение производной, y_h(x)- значение производной вычисленное по приближенной формуле при шаге h.

Величина погрешности зависит от точки x, в которой вычисляется производная, и от шага h, чем меньше шаг, тем естественно погрешность меньше. Обычно погрешность R(x,h) записывают одним из способов:

(2.6)

где, (x)h^k- называется главной частью погрешности аппроксимации, т.к. в формуле (2.6) это слагаемое при h<<1 будет гораздо больше второго, а величина k называется порядком погрешности или порядком точности аппроксимации относительно шага h.

Методы бисекции и Ньютона для задачи минимизации

Методы поиска минимума для гладких функций. Пусть f(x) является унимодальной функцией на отрезке [a,b] и имеет непрерывную производную на этом отрезке, а точка является точкой минимума. Следовательно, в точке имеем:

(2.6)

при этом

Следовательно задачу поиска минимума (2.1) мы можем заменить на задачу поиска корня уравнения (2.6), т.е. применить методы решения нелинейных уравнений к уравнению относительно производной функции.

а) метод бисекции. Так как и , то в точке минимума производная .меняет знак. Поэтому для поиска минимума отрезок делится на две части и исключается тот отрезок, где производная не меняет знак. Продолжая этот процесс уменьшается отрезок 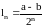внутри которого функция достигает минимума. Метод бисекции сходится по закону:

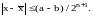(2.7)

б) метод Ньютона. Применение метода Ньютона для решения уравнения дает следующую расчетную формулу:

(2.8)

Он имеет квадратичную сходимость и итерационный процесс заканчивается при выполнении условия: .

Для сходимости метода необходимо и достаточно, чтобы выполнялись условия:

т.е. вторая и третья производные были знако постоянны на отрезке локализации.