Экзаменационный билет № 1

Математическое моделирование. Основные этапы математического моделирования

Математическое моделирование – предмет исследования объектов и явлений окружающего наш мир с помощью их приближенного описания на языке математики – математических моделей.

Процессы математического моделирования:

1. Построение модели

2. Постановка, исследование, решение математической задачи

3. Проверка модели на графике

Аппроксимация производных в крайних точках. Аппроксимация частных производных

Аппроксимацию производных конечными разностями в общем случае можно рассматривать как замену производной от функции y=f(x) производной от аппроксимирующей функции (x), (x)f(x), где в качестве аппроксимирующей функции используется интерполяционный многочлен: . Поэтому увеличивая степень интерполяционного многочлена n мы будем увеличивать порядок точности аппроксимации производной.

С помощью интерполяционного многочлена Лагранжа при равномерном распределении узлов были получены следующие формулы для аппроксимации производной с помощью центральных разностей второго и четвертого порядка точности:

(2.8)

где, y^(k)() - значение “к”-той производной в некоторой точке на отрезке [x_i-2,x_i+2].

В крайних точках таблицы или в крайних узлах нельзя использовать соотношения для центральных разностей (2.8). В этих точках используются односторонние формулы численного дифференцирования:

Метод оптимального пассивного поиска минимума функции

На отрезке [a,b] задается последовательность точек x₀,x₁,...,x_n, таких, что x_k=x₀+kh, k=1,...,n; x₀=a, x_n=b. В этих точках вычисляется значение функции f(x_k). За точку минимума принимается та точка x_k, для которой выполняется соотношение: .

Следовательно: Отсюда

Экзаменационный билет № 2

Точность вычислительного эксперимента. Источники и классификация погрешностей численного решения задачи

Источники погрешностей:

1. Погрешности задачи

Математические формулировки редко точно отображают реальные явления: обычно они дают более или менее идеализированные модели.

Иногда бывает так, что решить задачу в точной постановке трудно или даже невозможно. Тогда её заменяют близкой по результатам приближенной задачей. При этом возникает погрешность метода.

2. Остаточная погрешность

Погрешности, связанные с наличием бесконечных процессов в математическом анализе. Функции, фигурирующие в математических формулах, часто задаются в виде бесконечных последовательностей или рядов (например, sin x = x – x^3/3! + …). Более того, многие математические уравнения можно решить, лишь описав бесконечные процессы, пределы которых и являются искомыми решениями. Так как бесконечный процесс не может быть завершен в конечное число шагов, то мы вынуждены остановиться на некотором члене последовательности, считая его приближением к искомому решению.

3. Начальная погрешность

Погрешности, связанные с наличием в математических формулах числовых параметров, значения которых могут быть определены лишь приближенно. Таковы, например, все физические константы.

4. Погрешность округления

Погрешности, связанные с системой счисления. При изображении даже рациональных чисел в десятичной системе или другой позиционной системе справа от запятой может быть бесконечное число цифр (пример, бесконечная десятичная периодическая дробь). При вычислениях, можно использовать лишь конечное число этих цифр. Например, полагая 1/3 = 0,333, получаем погрешность 4*10^-4. Приходится округлять и конечные числа, имеющие большое количество знаков.

5. Погрешность действий

Погрешности, связанные с действиями над приближенными числами. Понятно, что, производя вычисления с приближенными числами, погрешности исходных данных в кокой-то мере мы переносим в результат вычислений. В этом отношении погрешности действий являются неустранимыми.

Обусловленность формул численного дифференцирования. Выбор оптимального шага

Так как величина y в формуле (2.10) является абсолютной предельной погрешностью входных данных, а (y)- абсолютной предельной погрешностью результата, то согласно определения абсолютного числа обусловленности _ для задачи численного дифференцирования из (2.10) имеем:

_=(y)/y=1/h,

т.е. задача плохо обусловлена, т.к. при при h0 число обусловленности стремится к бесконечности.

Полная абсолютная погрешность вычисления производной R(y_i) будет равна сумме погрешности (2.10) и погрешности формулы (2.8):

(2.11)

Первое слагаемое (погрешность вычислений) при уменьшении шага увеличивается, а второе слагаемое (погрешность самой формулы) уменьшается. Естественно будет такой шаг при котором полная погрешность будет минимальной., такой шаг называется оптимальным,

Оптимальный шаг h_опт определяется из условия минимума полной погрешности R(y_i), т.е. из решения уравнения R_h(y_i)=0, где значок h - говорит о том , что производная берется по h. Например, для формулы центральных разностей (2.8) из соотношения (2.11 имеем:

(2.12)

Естественно для каждой формулы численного дифференцирования будет своя формула для вычисления оптимального шага.

Если величина абсолютной предельной погрешности вычислений значений y определяется погрешностью округления ( машинным эпсилон ) (y)=_ y, то можем записать:

(2.13)

Обычно на практике полагают, что .

Градиентные методы в задачах минимизации

а) покоординатный спуск. В методе покоординатного спуска выбирается начальная точка x₀ с координатами . Фиксируются все координаты кроме первой и решается одномерная задача минимизации. Затем фиксируются все координаты кроме второй и опять решается задача одномерной минимизации и т.д. т.е. поочередно производится спускание по всем координатам x_i, до тех пор пока не выполнятся все условия:

, (2.4)

Если линия уровня имеет изломы, что соответствует “оврагам” на поверхности , то данный метод становится непригодным.

б) простой градиентный метод. В методе простого градиентного спуска выбирается начальная точка 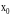и начальное значение шага h. В точке вычисляется градиент и делается шаг в направлении антиградиента:

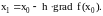. (2.5)

В результате вычисляется точка . Если выполняется условие , то в точке вычисляется градиент и делается шаг в направление антиградиента. Если условие не выполняется, то шаг h уменьшают до тех пор, пока это условие не будет выполнено. Процесс продолжается до выполнения третьего условия (2.4).

Недостатком метода является необходимость на каждом шаге вычислять значение градиента, что требует достаточно много времени.

в) метод наискорейшего спуска. Из начальной точки перпендикулярно линии уровня, т.е. в направлении антиградиента двигаются до тех пор, пока функция убывает, т.е. решают одномерную задачу минимизации для функции:

, (2.6)

где  выступает в качестве параметра.

В результате находится значение 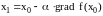, соответствующее минимальному значению функции на выбранной прямой. Затем вычислительный процесс повторяется для точки и т.д. Критерием окончания является третье условие (2.4).

Экзаменационный билет № 3

Приближенные числа. Абсолютная и относительная погрешности

Расчеты, как правило, производятся с приближенными значениями величин — приближенными числами. Уже исходные данные для расчета обычно даются с некоторыми погрешностями; в процессе расчета еще

накапливаются погрешности от округления, от применения приближенных формул и т.п. Разумная оценка погрешности при вычислениях позволяет указать оптимальное количество знаков, которые следует сохранять при расчетах, а также в окончательном результате.

Пусть a-точное значение некоторой величины, которое может быть и неизвестно, а^*-известное приближенное значение этой величины. Положительная величина называется абсолютной погрешностью величины a. Отношение абсолютной погрешности величины а к ее абсолютному значению называется относительной погрешностью.

Максимальное значение (а) называется предельной абсолютной погрешностью и обозначается (а). Соответственно предельная относительная погрешность равна:

.

Обычно слово “предельное” опускают и под абсолютной и относительной подразумевают абсолютную и относительную предельные погрешности.

Относительная погрешность приближенного числа связана с количеством его верных знаков. Количество верных знаков числа отсчитывается от первой значащей цифры числа до первой значащей цифры его абсолютной погрешности: например, число S = 20,7426 с абсолютной погрешностью

Δs = 0,0926 имеет три верных знака (2, 0, 7); остальные знаки - сомнительные.

Ориентировочно можно считать, что наличие только одного верного знака соответствует относительной погрешности порядка 10%, двух верных знаков — погрешности порядка 1%, трех верных знаков — погрешности порядка 0,1% и т. д. В математических таблицах все числа округлены до верных знаков, причем абсолютная погрешность не превосходит половины единицы последнего оставленного разряда. Например, если в таблице указано е=2,718,

то абсолютная погрешность не превосходит 0,5-10^-3.

В окончательных результатах вычислений обычно оставляют, кроме верных, один сомнительный знак.

В промежуточных результатах вычислений обычно сохраняют два-три сомнительных знака, чтобы не накапливать лишних погрешностей от округлений.

Численное интегрирование. Обусловленность задачи численного интегрирования

Определенным интегралом от функции f(x) на отрезке [a,b] называется предел интегральной суммы при n→∞ и ∆x→0:

где, n - количество элементарных отрезков [x_i-x_i-1], i=1,...,n; на которые разбивается отрезок интегрирования [a,b], ∆x_i=(x_i-x_i-1) - длина i-ого отрезка, е_i - точка на отрезке [x_i-1,x_i].

Когда функция f(x) задана аналитически в виде формулы и интеграл удается свести к табличному, то интеграл (2.1) вычисляется с помощью таблиц неопределенных интегралов и формулы Ньютона-Лейбница, например:

(2.2)

где F’(x) - первообразная, т.е. F’(x)=f(x).

Однако на практике обычно интеграл (2.2) не сводится известными приемами к табличному интегралу, даже тогда, когда под интегральная функция задана аналитически, не говоря уже о тех случаях, когда значения под интегральной f(x) заданы в виде таблицы. В этом случае используют численные методы

Относительное число обусловленности задачи численного интегрирования

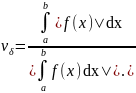
Проблема "оврагов" в задачах поиска минимума (?)

Выше нами были рассмотрены 3 варианта методов спуска, такие, как метод покоординатного спуска, метод градиентного спуска и метод наискорейшего спуска, и при этом наглядно показали, как хорошо они работают. В результате у вас могло сложиться впечатление, что проблема решена. На самом деле это не так. Все было хорошо потому, что был выбран "удобный" пример. Но посмотрите на рис. 11.4. На нем также показаны линии уровня некоторой функции. Линии уровня сильно вытянуты в одном направлении и сплющены в другом. Они напоминают рельеф местности с оврагом. Этот случай крайне неудобен для описанных выше методов.

Действительно, попытаемся найти наименьшее значение такой функции с помощью градиентного спуска. Двигаясь все время в направлении антиградиента, мы быстро спустимся на дно "оврага" и, поскольку движение идет хотя и маленькими, но конечными шагами, проскочим его. Оказавшись на противоположной стороне "оврага" и вычислив там градиент функции, мы будем вынуждены развернуться почти на 180° и сделать один или несколько шагов в обратном направлении. При этом мы снова проскочим дно "оврага" и вернемся на его первоначальную сторону. Продолжая этот процесс, мы вместо того, чтобы двигаться по дну "оврага" в сторону его понижения, будем совершать зигзагообразные скачки поперек "оврага", почти не приближаясь к цели. Таким образом, в случае "оврага" (этот нематематический термин прочно закрепился в литературе) описанные выше методы спуска оказываются неэффективными.

Для борьбы с "оврагами" был предложен ряд специальных приемов. Один из них заключается в следующем. Из двух близких точек совершают градиентный спуск на дно "оврага". Потом соединяют найденные точки прямой и делают вдоль нее большой (овражный) шаг. Из найденной точки снова спускаются на дно "оврага" и делают второй овражный шаг. В результате, двигаясь достаточно быстро вдоль "оврага", приближаемся к искомому наименьшему значению целевой функции (см. рис. 11.4). Такой метод достаточно эффективен для функций двух переменных, однако при большем числе переменных могут возникнуть трудности.

Рис. 11.4. Поиск наименьшего значения функции в случае "оврага"

Все описанные выше методы приспособлены к случаю, когда наименьшее значение функции достигается внутри рассматриваемой области, и становятся малоэффективными, если наименьшее значение достигается на границе или вблизи нее. Для решения таких задач приходится разрабатывать специальные методы. Мы не будем на них останавливаться. Вам должно быть и без того ясно, что большое число специальных методов - это признак слабости, а не силы. Ведь приступая к решению практической задачи, мы, как правило, не знаем всех ее особенностей и не можем сразу выбрать наиболее эффективный метод.