Параметры Стокса.
Исходное уравнение, полученное исключением из уравнений для х- и y-составляющих колебания электрического вектора, определяет эллипс более общего типа, причем его полуоси не параллельны осям х и у. Ориентация и отношение осей эллипса находится с помощью параметров Стокса:
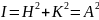
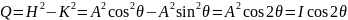
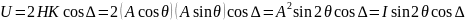
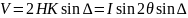
С
помощью элементарных алгебраических
преобразований можно показать, что для
полностью поляризованного пучка света
.
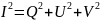Для частично поляризованного света можно определить степень поляризации:
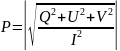
Подставляя параметры Стокса в уравнение колебаний, после преобразований получаем:
Где
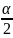– наименьший угол, который составляет
одна из осей эллипса с осью x.
Соотношение квадратов длин малой и
большой осей:
При этом параметры Н и К определяют амплитуды колебаний вектора электрического поля, которые при оптических частотах нельзя наблюдать непосредственно. Параметры Стокса связаны линейно с непосредственно измеряемыми с помощью фотоэлемента энергетическими характеристиками — они определяются реально измеряемой интенсивностью или разностью интенсивностей.
Матрицы Мюллера.
Четыре параметра Стокса, определяющие состояние поляризации луча, можно рассматривать как элементы матрицы размером 4X1. Такую матрицу будем называть столбцом (или вектором) Стокса и обозначать S:
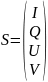
для приборов любого типа (поляроидной пленки, плоскость пропускания которой образует произвольный угол с осью; фазовой пластинки с произвольным запаздыванием и произвольной ориентацией быстрой оси; пластин, поворачивающих плоскость поляризации, роль которых могут играть некоторые органические жидкости) параметры Стокса для выходящего из прибора луча являются линейными функциями четырех параметров Стокса входного луча. Таким образом, можно написать следующие соотношения:
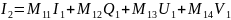
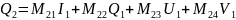
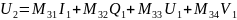
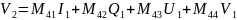
Здесь параметры Стокса, отмеченные индексом 1, относятся к входному лучу, а индексом 2 — к выходному лучу. Величины Ms с двумя нижними индексами описывают только характеристики прибора и его ориентацию. Эти четыре уравнения можно записать в матричном виде:
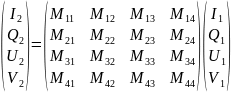
Или
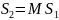
Здесь S1 — столбец Стокса для входного луча, a S2 — столбец Стокса, характеризующий выходящий из прибора луч, и М — матрица 4X4, описывающая ориентацию и характеристики прибора. Последнюю матрицу, характеризующую прибор, называют матрицей Мюллера. Эта матрица определяется только характеристиками прибора (объекта), через который проходит луч.
Выводы.
В данной работе были рассмотрены матричные методы описания прохождения света через объекты оптической системы. Применение матриц перемещения и преломления для нахождения конечного положения луча, а так же параметров Стокса для описания поляризации света значительно упрощает расчеты оптических систем. Однако данный метод имеет некоторые ограничения, которые необходимо учитывать при расчетах. Основным ограничением является возможность использования этого метода только для параксиальных пучков света.
Литература.
Джеррард А., Бёрч Дж.М. Введение в матричную оптику — М.: Мир, 1978. — 341 c.
Курс лекций по линейной алгебре
https://ru.wikipedia.org