Оглавление

Линейный оператор. 3

Матричная оптика. 4

Матрица перемещения τ. 7

Матрица преломления R. 8

Поляризация. 10

Параметры Стокса. 11

Матрицы Мюллера. 12

Выводы. 13

Литература. 14

Линейный оператор.

линейный оператор — обобщение линейной числовой функции (точнее, функции y=kx{\displaystyle y=kx}) на случай более общего множества аргументов и значений. Линейные операторы, в отличие от нелинейных, достаточно хорошо исследованы, что позволяет успешно применять результаты общей теории, так как их свойства не зависят от природы величин.

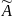Будем говорить, что в n-мерном линейном векторном пространстве   задан оператор   (преобразование, отображение), если каждому вектору 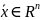 по некоторому правилу поставлен в соответствие единственный вектор 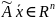 . 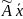- образ вектора  .

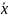Оператор называется линейным, если для любых векторов 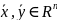  и для любого действительного числа α выполняется:

1. 

2. 

Пусть в пространстве задан базис   и задан линейный оператор . Тогда образы базисных векторов 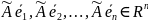  и их также можно разложить по заданному базису:

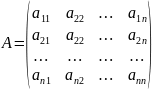–матрица линейного оператора в базисе.

Матрица оператора аналогична координатам вектора. При этом действие оператора на вектор равносильно умножению матрицы на столбец координат этого вектора в том же базисе.

Рассмотрим произвольный вектор пространства:

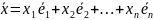
Его образ 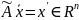, следовательно, его также можно разложить по заданному базису:

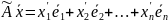
Обозначим:

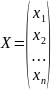- матрица-столбец координат ,

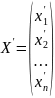- матрица-столбец координат образа 

Тогда, в силу линейности оператора:

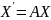- связь между координатами вектора и его образа.

С помощью матриц можно представить перемещение луча внутри оптической системы, при этом начальное и конечное его положение задаются координатами в столбце.

Матричная оптика.

Матричная оптика - математический аппарат расчета оптических систем различной сложности. Описание геометрического построения изображений в оптической системе справедливо в случае 2 приближений.

1. основное допущение всей геометрической оптики состоит в том, что длина волны света считается пренебрежимо малой и что распространение света можно описывать с помощью отдельных лучей, а не на языке волновых фронтов. Можно показать, что в свободном пространстве световые волны распространяются вдоль направления нормалей к волновым фронтам. Понятие геометрического луча представляет собой идеализацию этой волновой нормали. Из этих представлений следует принцип наикратчайшего оптического пути Ферма, которому подчиняется каждый луч. Суть этого принципа заключается в следующем: если мы рассмотрим окрестность любого небольшого участка траектории луча, то луч выбирает такой путь между двумя точками, который соответствует минимуму времени, затрачиваемому на прохождение расстояния между этими точками.

2. Будут рассматриваться лишь параксиальные лучи — лучи, которые при своем прохождении через оптическую систему остаются близкими к ее оси симметрии и почти параллельными ей. Тогда для синусов и тангенсов любых углов, образуемых этими лучами с оптической осью, можно использовать первый порядок разложения в ряд. Следовательно, эффекты третьего порядка, такие, как сферическая аберрация или кома, а также астигматизм, кривизна поля и дисторсия не учитываются.

Для описания прохождения параксиального луча через центрированную систему линз введем общепринятую в современной оптике систему декартовых координат: ось Oz, совпадающую с оптической осью системы, а также с главным направлением, вдоль которого распространяются лучи света, направим слева направо; ось Оу будем считать расположенной в плоскости страницы и направленной вверх, а ось Ох перпендикулярной этой плоскости.

Траектория луча, поскольку он проходит через различные преломляющие поверхности системы, будет состоять из последовательности прямых линий. Каждая из этих прямых определяется координатами одной принадлежащей ей точки и углом, который составляет данная прямая линия с осью Oz. Выберем заранее любую плоскость z = const, перпендикулярную оси Oz, и назовем ее опорной плоскостью (ОП). Тогда Луч можно определить по отношению к опорной плоскости двумя параметрами: высотой, на которой этот луч пересекает опорную плоскость (координата y) и углом 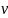, который он составляет с осью Oz. Угол измеряется в радианах и считается положительным, если он соответствует вращению против часовой стрелки от положительного направления оси Oz к направлению, в котором свет распространяется вдоль луча (рис. 1). 

Рис. 1. Система координат.

На практике удобнее не рассчитывать все лучи по отношению к одной ОП, а на каждом этапе расчета выбирать новую ОП. Это означает, что параметры луча непрерывно переносятся с одной ОП на другую, по мере того как мы рассматриваем различные элементы системы. Однако если требуется выполнить полный расчес системы в целом, то возникает вопрос о полной матрице преобразования лучей, которая преобразовывала бы все необходимые параметры луча от выбранной нами входной ОП непосредственно к выбранной выходной ОП. 

Поскольку луч проходит через систему преломляющих линз, то для исследования его поведения необходимо рассмотреть только два основных процесса: 

1. Перемещение между двумя преломляющими поверхностями – оптический промежуток. На таком участке пути луч проходит по прямой линии от одной преломляющей поверхности к другой. Область между поверхностями характеризуется ее толщиной t и показателем преломления n среды, через которую проходит луч. 

2. Преломление на граничной поверхности между двумя областями с различными показателями преломления. Для того чтобы определить величину отклонения прошедшего луча, необходимо знать радиус кривизны преломляющей поверхности и два значения показателя преломления граничащих сред. 

Уравнения для двух оптических элементов (преломляющая поверхность и оптический промежуток) являются линейными, и, следовательно, их можно записать в матричной форме: 

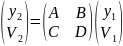
где y и V – высота и угол луча в начальном и конечном положении. Матричные элементы таковы, что определитель (AD - ВС) равен единице. При прохождении луча в обратном направлении матричное уравнение обращается и принимает вид:

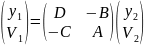
Таким образом, каждому элементу оптической системы можно поставить в соответствие свою унимодулярную матрицу преобразования лучей. Для того чтобы получить общую матрицу преобразования лучей, описывающую всю оптическую систему в целом, следует перемножить в правильной последовательности все матрицы элементарных перемещений и преломлений, встречающихся в системе. Такая система может представлять собой все что угодно, начиная от единственной тонкой линзы и кончая сложной оптической системой.