Оглавление

ВВЕДЕНИЕ…………………………………………………….4

1. КРАТНЫЕ ИНТЕГРАЛЫ…………………………………..5

1.1. Двойные интегралы……………………………………….5

1.2. Тройные интегралы………………………………………13

2. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ………………………21

2.1. Криволинейные интегралы первого рода……………….21

2.2. Криволинейные интегралы второго рода……………….23

3. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ……………………….29

3.1. Поверхностные интегралы первого рода………………..29

3.2. Поверхностные интегралы второго рода………………..36

4. ЗАДАНИЕ К КУРСОВОЙ РАБОТЕ………………………44

БИБЛИОГРАФИЧЕСКИЙ СПИСОК………………………..45

ПРИЛОЖЕНИЕ………………………………………………..46

Введение

В программу по высшей математике для большинства технических специальностей входит выполнение курсовой работы. Она приходится на третий семестр, когда студенты изучают кратные, криволинейные и поверхностные интегралы, а на их основе – теорию поля. Именно по этим разделам и составлена курсовая работа.

В курсовой работе требуется рассчитать технические параметры модели летательного аппарата. Подобные вычисления могут потребоваться при решении реальных инженерных задач, где необходимо исследовать оболочки или однородные объекты из различных материалов с точки зрения механики, а также воздействие внешних потоков среды или поля, что пересекается с задачами физики.

Сложность выполнения курсовой работы связана с необходимостью изучения большого объема материала из различных разделов высшей математики.

Методические указания содержат необходимые теоретические основы математики, особое внимание уделено физическим и техническим приложениям. Конечно, для более глубокого понимания теории потребуется изучение литературы, но все необходимые для курсовой работы определения и формулы в этих указаниях приведены. Дано много различных примеров с подробными решениями, часть рассматриваемых задач идентична заданиям курсовой работы, что облегчит ее выполнение.

Указания соответствуют уровню преподавания курса и могут быть использованы также и как конспект лекций.

1. Кратные интегралы

1.1. Двойные интегралы

Рис. 1.1

Пусть D - ограниченная замкнутая область в плоскости xOy. Функция z=f(x,y) определена и ограничена в области D (рис.1.1). Разобьем эту область на n частей и обозначим их площади соответственно ∆S₁, ∆S₂, ∆S₃, . . . , ∆S_n. В каждой части ∆S_i возьмем произвольно точку M_i (x_i, y_i) и составим сумму

. (1.1)

Эта сумма называется интегральной суммой функции f(x, y) в области D.

Определение. Если при любом разбиении области D на части ∆S_i и произвольном выборе точек M_i(x_i,y_i) существует предел последовательности сумм (1.1) при условии, что максимальный из диаметров частей ∆S_i стремится к нулю, то этот общий предел называют двойным интегралом от функции f(x, y) по области D и обозначают символом

.

Итак,

.

Область D называется областью интегрирования, а dS – элементом площади.

Свойства

Двойной интеграл обладает всеми основными свойствами обыкновенного интеграла функции одной переменной на отрезке.

1. Постоянный множитель можно выносить за знак двойного интеграла,

.

2. Двойной интеграл от суммы функций равен сумме двойных интегралов,

.

3

Рис. 1.2

. Область интегрирования можно разбить на части (рис.1.2),

.

Геометрический смысл двойного интеграла

Если f(x, y) > 0, то двойной интеграл от функции f(x, y) по области D равен объему тела, ограниченного сверху поверхностью z = f(x, y), снизу плоскостью хОу и сбоку прямой цилиндрической поверхностью, вырезающей на плоскости хОу область D,

.

Если f(x, y) = 1, то двойной интеграл равен площади области D, т.е.

.

Если в области D функция f(x, y) меняет знак, то область разбивается на две части: 1) область D₁, где f(x, y) > 0; 2) область D₂, где f(x, y) < 0. Предположим, что области D₁ и D₂ таковы, что двойные интегралы по этим областям существуют. Тогда интеграл по области D₁ будет положителен и равен объему тела, лежащему выше плоскости хОу. Интеграл по области D₂ будет отрицателен и по абсолютной величине равен объему тела, лежащего ниже плоскости хОу. Следовательно, интеграл по всей области D будет выражать разность этих объемов.

В ычисление двойного интеграла

1. В декартовых координатах элемент площади равен площади прямоугольника со сторонами dx и dy, т.е. dS =dxdy, тогда двойной интеграл записывают в виде

.

В

Рис. 1.3

общем случае область интегрирования сводится путем разбиения на части к двум основным видам.

Рис. 1.4

Первый вид - область D ограничена слева и справа прямыми х = a и х = b (a < b), а снизу и сверху - непрерывными кривыми y = y_(x) и y = y₂(x) (y₁(x) < y₂(x)). При этом каждая из кривых y₁(x) и y₂(x) пересекаются любой вертикальной прямой только в одной точке (рис.1.4). Для такой области двойной интеграл вычисляется по формуле:

. (1.2)

Последний интеграл называется двукратным и сначала вычисляется внутренний интеграл , в котором х считается постоянным, а затем вычисляется внешний интеграл по dx (пример 1.1), т.е.

.

Рис. 1.5

Второй вид - область D ограничена снизу и сверху прямыми y = c и y = d (c < d), а слева и справа - непрерывными кривыми x = x₁(y) и x = x₂(y) (x₁(y) < x₂(y)). При этом каждая из кривых x₁(y) и x₂(y) пересекаются любой горизонтальной прямой только в одной точке (рис.1.5). Для такой области справедлива формула:

2. Полярные координаты ρ и φ связаны с прямоугольными координатами х, у соотношениями

x = ρ cos φ, y = ρ sin φ.

Э

ρdφ

dS

dφ

O dρ ρ

лемент площади dS можно считать равным площади прямоугольника со сторонами dρ и ρdφ, последнее есть длина дуги окружности радиуса ρ с центральным углом dφ (рис.1.6), т.е.

dS = ρ dρ dφ,

т

Рис. 1.6

огда двойной интеграл вычисляется по формуле

ρ cos φ, ρ sin φ) ρ dρ dφ.

Рис. 1.7

Е

Рис. 1.7

сли область интегрирования D ограничена лучами φ = α и φ = β (α<β) и двумя кривыми ρ = ρ₁(φ) и ρ = ρ₂(φ), где ρ₁(φ) и ρ₂(φ) - однозначные функции при α≤ φ ≤ β и ρ₁(φ)≤ρ₂(φ) (рис. 1.7), то двойной интеграл вычисляется по формуле:

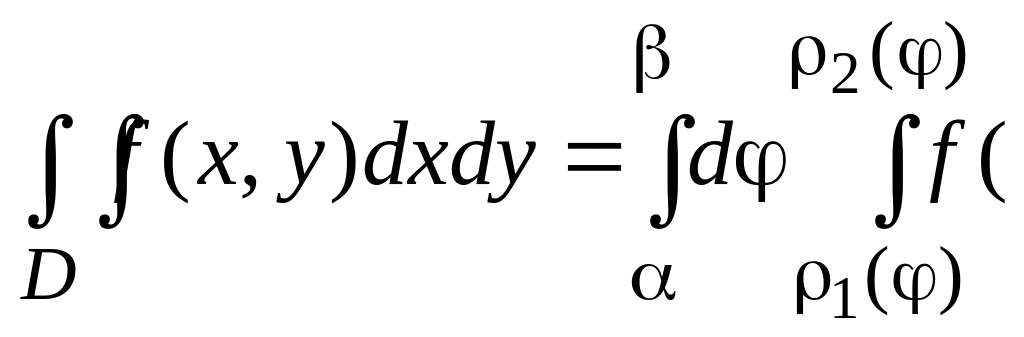ρ cos φ, ρ sin φ) ρ dρ (1.3)

(пример 1.2).

Приложения двойного интеграла

1. Площадь поверхности

Пусть поверхность σ задана уравнением z = f(x, y), где f(x, y) имеет непрерывные частные производные первого порядка в некоторой замкнутой ограниченной области D плоскости хОу. Площадь поверхности σ вычисляется по формуле

S =

Если уравнение поверхности задано в виде х = ψ (y, z) или у = η (х, z), то площадь вычисляется по формулам:

S = ,

S = ,

где D’ и D’’ - проекции на плоскостях yOz и xOz данной поверхности.

2. Масса пластины

Если пластина занимает на плоскости хОу область D и имеет переменную поверхностную плотность γ = γ(х, у), то масса m пластины выражается двойным интегралом

.

3. Статические моменты

Статические моменты пластины относительно осей Ох и Оу вычисляются по формулам:

, .

4. Координаты центра тяжести

Координаты центра тяжести пластины, имеющей плотность γ = γ(х, у), вычисляются по формулам:

, ,

где m - масса пластины, М_х, М_y - ее статические моменты.

Если пластина однородная, т.е. γ = const, то эти формулы принимают вид

, ,

где S - площадь пластины.

5. Моменты инерции

Моменты инерции пластины относительно осей Ох и Оу вычисляются по формулам:

, .

Момент инерции относительно начала координат равен

.

6. Геометрические моменты инерции

Полагая в формулах для I_x, I_y и I_o γ(х, у) = 1, получим формулы для вычисления геометрических моментов инерции:

, , .

Пример 1.1. Вычислить двойной интеграл , если область D ограничена прямыми y = x, y = 2x, x = 1.

Рис. 1.8

Решение. Построим область интегрирования D (рис.1.8). Область принадлежит первому виду, поэтому интеграл будем вычислять по формуле (1.2). В данном случае a =0, b=1, y₁(x) = x, y₂(x) = 2x, подынтегральная функция - f(x, y) = xy.

.

Вычислим сначала внутренний интеграл, считая х постоянным, а затем найдем внешний интеграл.

.

Ответ:3/8.

Пример 1.2. Вычислить двойной интеграл , если область D ограничена окружностями x² + y² = x, x² + y² = 2x.

Решение. Преобразуем уравнения окружностей:

x² + y² = x 



 ,

Рис. 1.9

x² + y² = 2x 



.

Первая окружность имеет центр в точке (1/2; 0) и радиус 1/2, вторая окружность имеет центр в точке (1; 0) и радиус 1 (рис. 1.9).

Запишем уравнения окружностей в полярных координатах:

x² + y² = x  ρ² cos²φ + ρ² sin²φ = ρcosφ  ρ = cosφ ;

x² + y² = 2x  ρ = 2cosφ.

Для точек области D полярный угол  изменяется от - до , а полярный радиус ρ от кривой ρ₁ = cosφ до кривой ρ₂ = 2cosφ . Найдем интеграл по формуле (1.3).

.

Ответ: .