Вопрос 4

Ускорение в декартовой системе координат: , проекции и ускорения на оси декартовой системы координат будут , составляющие ускорения, параллельные осям координат, определятся как , а численное значение ускорения будет равно: . Проекцию ускорения на ось, совпадающую по направлению с вектором скорости. для определения характера движения точки (т.е. ускоренно или замедленно она движется) можно в данном случае найти, в виде:

.

Равноускоренное движение - движение с постоянным ускорением (a = const); движение, при котором за равные промежутки времени скорость меняется одинаково (по величине и направлению).

Полное, тангенциальное и нормальное ускорения. При криволинейном движении полное ускорение материальной точки раскладывается на две составляющих: нормальное ускорение и тангенциальное ускорение . , ., а – полное ускорение.

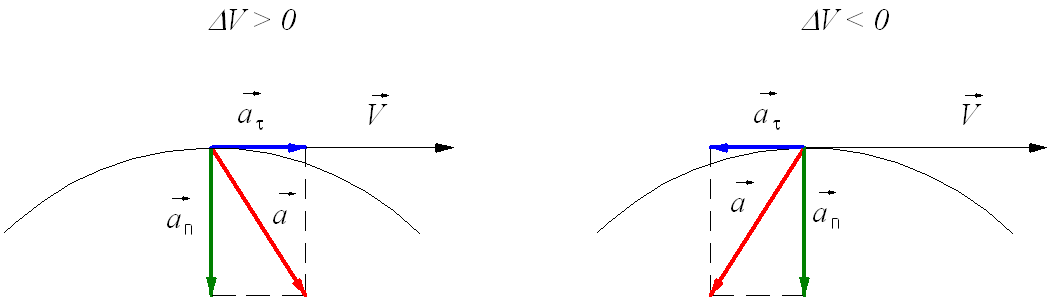
(1)Тангенциальное ускорение - ускорение, направленное параллельно мгновенной скорости и изменяющее ее по величине

(2)Тангенциальное (касательное) ускорение – компонента ускорения, направленная по касательной к траектории движения. Характеризует изменение модуля скорости в отличие от нормальной компоненты, характеризующей изменение направления скорости. Тангенциальное ускорение равно произведению единичного вектора, направленного по скорости движения, на производную модуля скорости по времени. Таким образом, направлено в ту же сторону, что и вектор скорости при ускоренном движении (положительная производная) и в противоположную при замедленном (отрицательная производная).

, согласно вики Величина тангенциального ускорения связана с величиной углового ускорения соотношением:

, где  — радиус траектории.

Нормальное ускорение (центростремительное ускорение) — компонента ускорения точки, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной. Направлено к центру кривизны траектории, чем и обусловлен термин. По величине равно квадрату скорости, поделённому на радиус кривизны. Термин «центростремительное ускорение» эквивалентен термину «нормальное ускорение». Ту составляющую суммы сил, которая обуславливает это ускорение, называют центростремительной силой.

. R – радиус кривизны.

Радиус кривизны — величина, обратная кривизне. Радиус кривизны характеризует величину соответствия кривой от прямой. Чем больше радиус кривизны, тем больше кривая похожа на прямую.

Радиус кривизны определяется для конкретной точки конкретной кривой он равняется радиусу соприкасающейся окружности.

Вопрос 5

Вращательным движением абсолютно твердого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела движутся в плоскостях, перпендикулярных к неподвижной прямой, называемой осью вращения, и описывают окружности, центры которых лежат на этой оси.

Угловой скоростью вращения называется вектор, численно равный первой производной угла поворота тела по времени и направленный вдоль оси вращения по правилу правого винта:

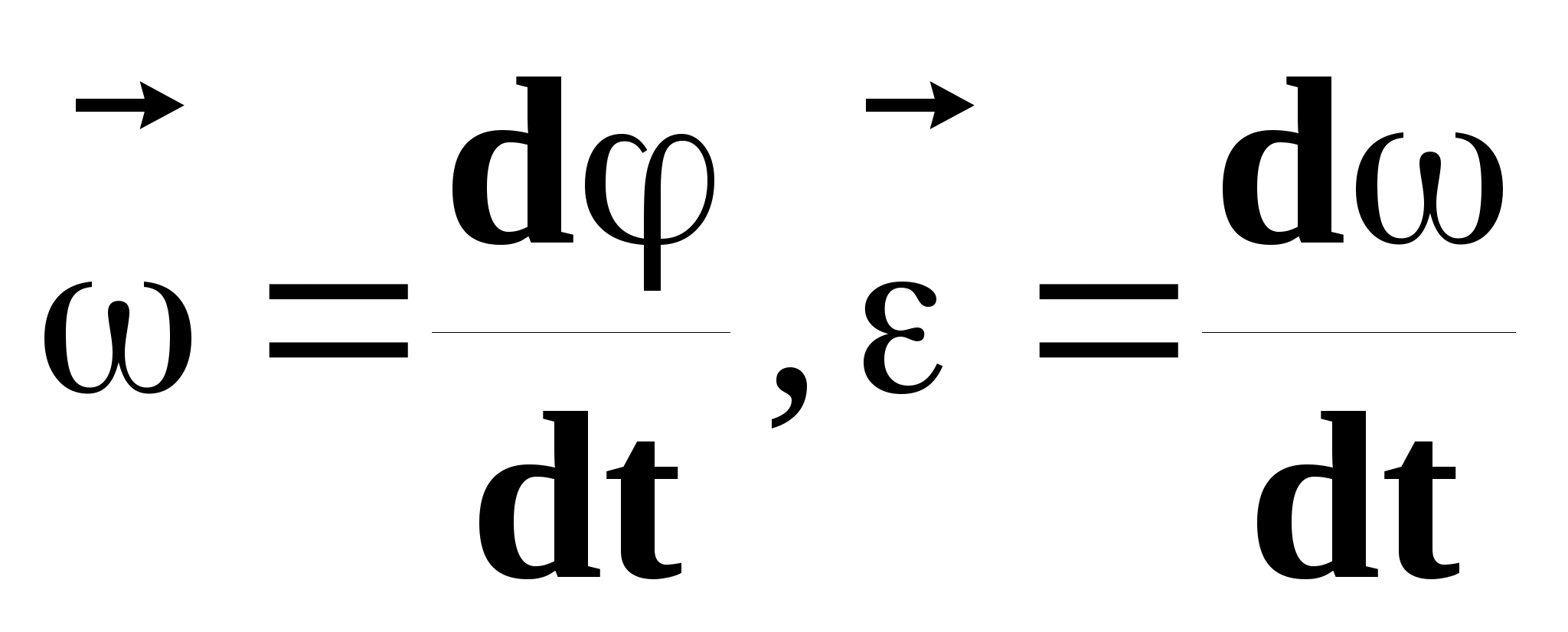
Связь мгновенной угловой скорости ω связана с угловым ускорением ε :

ω = ε*t

Единица измерения угловой скорости радиан в секунду (рад/с). Таким образом, вектор ω определяет направление и быстроту вращения. Если ω=const, то вращение называется равномерным.

При равномерном вращении его можно охарактеризовать периодом вращения Т –временем, за которое точка тела совершает один полный оборот, т.е. поворачивается на угол 2π (360 градусов):

Число полных оборотов, совершаемых телом при равномерном движении по окружности, в единицу времени называется частотой вращения:

Откуда

Связь между линейной и угловой скоростями. Точка, лежащая на окружности радиусом R, за один оборот пройдет путь . Поскольку время одного оборота тела есть период T, то модуль линейной скорости точки можно найти так:

Так как , то

Модуль ускорения точки тела, движущейся равномерно по окружности, можно выразить через угловую скорость тела и радиус окружности:

Следовательно,